Branch and cut: Difference between revisions
Peterghaddad (talk | contribs) mNo edit summary |
No edit summary |
||
| (33 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
Author: Lindsay Siegmundt, Peter Haddad, Chris Babbington, Jon Boisvert, Haris Shaikh (SysEn | Author: Lindsay Siegmundt, Peter Haddad, Chris Babbington, Jon Boisvert, Haris Shaikh (SysEn 5800 Fall 2020) | ||
== Introduction == | == Introduction == | ||
The Branch and Cut | The Branch and Cut methodology was discovered in the 90s as a way to solve/optimize Mixed-Integer Linear Programs (Karamanov, Miroslav)<ref>Karamanov, Miroslav. “Branch and Cut: An Empirical Study.” ''Carnegie Mellon University'' , Sept. 2006, https://www.cmu.edu/tepper/programs/phd/program/assets/dissertations/2006-operations-research-karamanov-dissertation.pdf.</ref>. This concept is comprised of two known optimization methodologies - Branch and Bound and Cutting Planes. Utilizing these two tools allows for the Branch and Cut to find an optimal solution through relaxing the problem to produce the upper bound. Relaxing the problem allows for the complex problem to be simplified in order for it to be solve more easily. Furthermore, the upper bound represents the highest value the objective can take in order to be feasible. The optimal solution is found when the objective is equal to the upper bound (Luedtke, Jim)<ref>Luedtke, Jim. “The Branch-and-Cut Algorithm for Solving Mixed-Integer Optimization Problems.” ''Institute for Mathematicians and Its Applications'', 10 Aug. 2016, https://www.ima.umn.edu/materials/2015-2016/ND8.1-12.16/25397/Luedtke-mip-bnc-forms.pdf.</ref>. This methodology is critical to the future of optimization since it combines two common tools in order to utilize each component in order to find the optimal solution. Moving forward, the critical components of different methodologies could be combined in order to find optimality in a more simple and direct manner. | ||
== Methodology & Algorithm == | == Methodology & Algorithm == | ||
=== Methodology - | === Methodology === | ||
{| class="wikitable" | |||
|+Abbreviation Details | |||
!Acronym | |||
!Expansion | |||
|- | |||
|LP | |||
|Linear Programming | |||
|- | |||
|B&B | |||
|Branch and Bound | |||
|} | |||
==== Most Infeasible Branching: ==== | |||
Most infeasible branching is a very popular method that picks the variable with fractional part closest to <math>0:5</math>, i.e.,<math> si = 0:5-|xA_i- xA_i-0:5|</math><ref>Branching rules revisited Tobias Achterberga;∗, Thorsten Kocha, Alexander Martinb https://www-m9.ma.tum.de/downloads/felix-klein/20B/AchterbergKochMartin-BranchingRulesRevisited.pdf</ref>. Most infeasible branching picks a variable where the least tendency can be recognized to which side the variable should be rounded. However, the performance of this method is not any superior to the rule of selecting a variable randomly. | |||
==== '''Strong Branching:''' ==== | |||
For each fractional variable, strong branching tests the dual bound increase by computing the LP relaxations result from the branching on that variable. As a branching variable for the current node, the variable that leads to the largest increases is selected. Despite its obvious simplicity, strong branching is so far the most powerful branching technique in terms of the number of nodes available in the B&B tree, this effectiveness can however be accomplished only at the cost of computation.<ref>A Branch-and-Cut Algorithm for Mixed Integer Bilevel Linear Optimization Problems and Its Implementation<nowiki/>https://coral.ise.lehigh.edu/~ted/files/papers/MIBLP16.pdf</ref> | |||
==== '''Pseudo Cost:''' ==== | |||
[[File:Image.png|thumb|Pure psuedo cost branching]] | |||
=== '''Algorithm | Another way to approximate a relaxation value is by utilizing a pseudo cost method. The pseudo-cost of a variable is an estimate of the per unit change in the objective function from making the value of the variable to be rounded up or down. For each variable we choose variable with the largest estimated LP objective gain<ref>Advances in Mixed Integer Programming http://scip.zib.de/download/slides/SCIP-branching.ppt</ref>. | ||
==='''Algorithm'''=== | |||
Branch and Cut for is a variation of the Branch and Bound algorithm. Branch and Cut incorporates Gomery cuts allowing the search space of the given problem. The standard Simplex Algorithm will be used to solve each Integer Linear Programming Problem (LP). | Branch and Cut for is a variation of the Branch and Bound algorithm. Branch and Cut incorporates Gomery cuts allowing the search space of the given problem. The standard Simplex Algorithm will be used to solve each Integer Linear Programming Problem (LP). | ||
<math>min: c^tx | |||
</math> | |||
<math>s.t. Ax < b | |||
</math> | |||
<math>x \geq 0 | |||
</math> | |||
<math>x_i = int, i = 1,2,3...,n | |||
</math> | |||
Above is a mix-integer linear programming problem. x and c are a part of the n-vector. These variables can be set to 0 or 1 allow binary variables. The above problem can be denoted as <math>LP_n </math> | |||
Below is an Algorithm to utilize the Branch and Cut algorithm with Gomery cuts and Partitioning: | Below is an Algorithm to utilize the Branch and Cut algorithm with Gomery cuts and Partitioning: | ||
'''Step 0:''' | |||
Upper Bound = ∞ | Upper Bound = ∞ | ||
Lower Bound = -∞ | Lower Bound = -∞ | ||
'''Step 1. Initialize:''' | |||
Set the first node as <math>LP_0</math> while setting the active nodes set as <math>L</math>. The set can be accessed via <math>LP_n </math> | Set the first node as <math>LP_0</math> while setting the active nodes set as <math>L</math>. The set can be accessed via <math>LP_n </math> | ||
==== Step 2. Terminate: ==== | ===='''Step 2. Terminate:'''==== | ||
Step 3. Iterate through list L: | |||
While <math>L</math> is not empty (i is the index of the list of L), then: | While <math>L</math> is not empty (i is the index of the list of L), then: | ||
'''Step 3.1. Convert to a Relaxation:''' | |||
'''Solve 3.2.''' | |||
Solve for the Relaxed | Solve for the Relaxed | ||
'''Step 3.3.''' | |||
If Z is infeasible: | If Z is infeasible: | ||
Return to step 3. | Return to step 3. | ||
else: | else: | ||
Continue with solution Z. | Continue with solution Z. | ||
Step | '''Step 4. Cutting Planes:''' | ||
If a cutting plane is found: | If a cutting plane is found: | ||
then add to the | then add to the Linear Relaxation problem (as a constraint) and return to step 3.2 | ||
Else: | Else: | ||
Continue. | Continue. | ||
'''Step 5. Pruning and Fathoming:''' | |||
(a)If ≥ Z:, then go to step 3. | |||
If Z^l <= Z AND X_i is an integral feasible: | If Z^l <= Z AND X_i is an integral feasible: | ||
Z = Z^i | Z = Z^i | ||
Remove all Z^i from Set(L) | Remove all Z^i from Set(L) | ||
'''Step 6. Partition''' | |||
Let <math>D^{lj=k}_{j=1}</math> be a partition of the constraint set <math>D</math> of problem <math>LP_l</math>. Add problems <math>D^{lj=k}_{j=1}</math> to L, where <math>LP^l_j</math> is <math>LP_l</math> with feasible region restricted to <math>D^l_j</math> and <math>Z_{lj}</math> for j=1,...k is set to the value of <math>Z^l</math> for the parent problem l. Go to step 3.<ref name=":0">Benders, J. F. (Sept. 1962), "Partitioning procedures for solving mixed-variables programming problems", Numerische Mathematik 4(3): 238–252.</ref> | |||
==Numerical Example== | |||
First, list out the MILP: | |||
<math>min \ z=-4x_1-7x_2</math> | |||
<math>6x_1 + x_2 \leq13</math> | |||
<math>-x_1+4x_2\leq5</math> | |||
<math>x_1,x_2\geq0</math> | |||
Solution to original LP | |||
<math>z =-19.56, x_1=1.88, x_2=1.72 </math> | |||
Branch on x<sub>1</sub> to generate sub-problems | |||
<math>min \ z=-4x_1-7x_2</math> | |||
<math>6x_1 + x_2 \leq13</math> | |||
<math>-x_1+4x_2\leq5</math> | |||
<math>x_1\geq2</math> | |||
<math>x_1,x_2\geq0</math> | |||
Solution to fist branch sub-problem | |||
<math>z =-15, x_1=2, x_2=1</math> | |||
<math>min \ z=-4x_1-7x_2</math> | |||
<math>6x_1 + x_2 \leq13</math> | |||
<math>-x_1+4x_2\leq5</math> | |||
<math>x_1\leq1</math> | |||
<math>x_1,x_2\geq0</math> | |||
Solution to second branch sub-problem | |||
<math>z =-14.5, x_1=1, x_2=1.5</math> | |||
Adding a cut | |||
<math>min \ z=-4x_1-7x_2</math> | |||
<math>6x_1 + x_2 \leq13</math> | |||
<math>-x_1+4x_2\leq5</math> | |||
<math>2x_1+x_2\leq 3</math> | |||
<math>x_1\leq1</math> | |||
<math>x_1,x_2\geq0</math> | |||
Solution to cut LP | |||
<math>z=-13.222,x_1=.778,x_2=1.444</math> | |||
==Application== | |||
Several of the Branch and Cut applications are described below in more detail and how they can be used. These applications serve as methods in which Branch and Cut can be used to optimize various problems efficiently. | |||
=== '''Combinatorial Optimization''' === | |||
Combinatorial Optimization is a great application for Branch and Cut. This style of optimization is the methodology of utilizing the finite known sets and information of the sets to optimize the solution. The original intent for this application was for maximizing flow as well as in the transportation industry (Maltby and Ross). This combinatorial optimization has also taken on some new areas where it is used often. Combinatorial Optimization is now an imperative component in studying artificial intelligence and machine learning algorithms to optimize solutions. The finite sets that Combinatorial Optimization tends to utilize and focus on includes graphs, partially ordered sets, and structures that define linear independence call matroids.<ref>[https://brilliant.org/wiki/combinatorial-optimization/ Maltby, Henry, and Eli Ross. “Combinatorial Optimization.” ''Brilliant Math & Science Wiki'', https://brilliant.org/wiki/combinatorial-optimization/.]</ref> | |||
=== | === '''Bender’s Decomposition''' === | ||
Bender’s Decomposition is another Branch and Cut application that is utilized widely in Stochastic Programming. Bender’s Decomposition is where you take the initial problem and divide into two distinct subsets. By dividing the problem into two separate problems you are able to solve each set easier than the original instance (Benders). Therefore the first problem within the subset created can be solved for the first variable set. The second sub problem is then solved for, given that first problem solution. Doing this allows for the sub problem to be solved to determine whether the first problem is infeasible (Benders). Bender’s cuts can be added to constrain the problem until a feasible solution can be found.<ref name=":0" /> | |||
== | === '''Large-Scale Symmetric Traveling Salesmen Problem''' === | ||
The Large-Scale Symmetric Traveling Salesmen Problem is a common problem that was always looked into optimizing for the shortest route while visiting each city once and returning to the original city at the end. On a larger scale this style of problem must be broken down into subsets or nodes (SIAM). By constraining this style of problem such as the methods of Combinatorial Optimization, the Traveling Salesmen Problem can be viewed as partially ordered sets. By doing this on a large scale with finite cities you are able to optimize the shortest path taken and ensure each city is only visited once.<ref>Society for Industrial and Applied Mathematics. “SIAM Rev.” ''SIAM Review'', 18 July 2006, https://epubs.siam.org/doi/10.1137/1033004</ref> | |||
== | === '''Submodular Function''' === | ||
Submodular Function is another function in which is used throughout artificial intelligence as well as machine learning. The reason for this is because as inputs are increased into the function the value or outputs decrease. This allows for a great optimization features in the cases stated above because inputs are continually growing. This allows for machine learning and artificial intelligence to continue to grow based on these algorithms (Tschiatschek, Iyer, and Bilmes)<ref>S. Tschiatschek, R. Iyer, H. Wei and J. Bilmes, Learning Mixtures of Submodular Functions for Image Collection Summarization, NIPS-2014.</ref>. By enforcing new inputs to the system the system will learn more and more to ensure it optimizes the solution that is to be made.<ref>A. Krause and C. Guestrin, Beyond Convexity: Submodularity in Machine Learning, Tutorial at ICML-2008</ref> | |||
== Conclusion | ==Conclusion== | ||
The Branch and Cut is an optimization algorithm used to optimize integer linear programming. It combines two other optimization algorithms - branch and bound and cutting planes in order to utilize the results from each method in order to create the most optimal solution. There are three different methodologies used within the specific method - most infeasible branching, strong branching, and pseudo code. Furthermore, Branch and Cut can be utilized it multiple scenarios - Submodular function, large-scale symmetric traveling salesmen problem, bender's decomposition, and combination optimization which increases the impact of the methodology. | |||
== | ==Reference== | ||
<references /> | |||
Latest revision as of 07:38, 21 December 2020
Author: Lindsay Siegmundt, Peter Haddad, Chris Babbington, Jon Boisvert, Haris Shaikh (SysEn 5800 Fall 2020)
Introduction
The Branch and Cut methodology was discovered in the 90s as a way to solve/optimize Mixed-Integer Linear Programs (Karamanov, Miroslav)[1]. This concept is comprised of two known optimization methodologies - Branch and Bound and Cutting Planes. Utilizing these two tools allows for the Branch and Cut to find an optimal solution through relaxing the problem to produce the upper bound. Relaxing the problem allows for the complex problem to be simplified in order for it to be solve more easily. Furthermore, the upper bound represents the highest value the objective can take in order to be feasible. The optimal solution is found when the objective is equal to the upper bound (Luedtke, Jim)[2]. This methodology is critical to the future of optimization since it combines two common tools in order to utilize each component in order to find the optimal solution. Moving forward, the critical components of different methodologies could be combined in order to find optimality in a more simple and direct manner.
Methodology & Algorithm
Methodology
| Acronym | Expansion |
|---|---|
| LP | Linear Programming |
| B&B | Branch and Bound |
Most Infeasible Branching:
Most infeasible branching is a very popular method that picks the variable with fractional part closest to $ 0:5 $, i.e.,$ si = 0:5-|xA_i- xA_i-0:5| $[3]. Most infeasible branching picks a variable where the least tendency can be recognized to which side the variable should be rounded. However, the performance of this method is not any superior to the rule of selecting a variable randomly.
Strong Branching:
For each fractional variable, strong branching tests the dual bound increase by computing the LP relaxations result from the branching on that variable. As a branching variable for the current node, the variable that leads to the largest increases is selected. Despite its obvious simplicity, strong branching is so far the most powerful branching technique in terms of the number of nodes available in the B&B tree, this effectiveness can however be accomplished only at the cost of computation.[4]
Pseudo Cost:
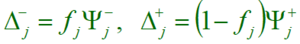
Another way to approximate a relaxation value is by utilizing a pseudo cost method. The pseudo-cost of a variable is an estimate of the per unit change in the objective function from making the value of the variable to be rounded up or down. For each variable we choose variable with the largest estimated LP objective gain[5].
Algorithm
Branch and Cut for is a variation of the Branch and Bound algorithm. Branch and Cut incorporates Gomery cuts allowing the search space of the given problem. The standard Simplex Algorithm will be used to solve each Integer Linear Programming Problem (LP).
$ min: c^tx $
$ s.t. Ax < b $
$ x \geq 0 $
$ x_i = int, i = 1,2,3...,n $
Above is a mix-integer linear programming problem. x and c are a part of the n-vector. These variables can be set to 0 or 1 allow binary variables. The above problem can be denoted as $ LP_n $
Below is an Algorithm to utilize the Branch and Cut algorithm with Gomery cuts and Partitioning:
Step 0:
Upper Bound = ∞ Lower Bound = -∞
Step 1. Initialize:
Set the first node as $ LP_0 $ while setting the active nodes set as $ L $. The set can be accessed via $ LP_n $
Step 2. Terminate:
Step 3. Iterate through list L:
While $ L $ is not empty (i is the index of the list of L), then:
Step 3.1. Convert to a Relaxation:
Solve 3.2.
Solve for the Relaxed
Step 3.3.
If Z is infeasible: Return to step 3. else: Continue with solution Z.
Step 4. Cutting Planes:
If a cutting plane is found: then add to the Linear Relaxation problem (as a constraint) and return to step 3.2 Else: Continue.
Step 5. Pruning and Fathoming:
(a)If ≥ Z:, then go to step 3.
If Z^l <= Z AND X_i is an integral feasible: Z = Z^i Remove all Z^i from Set(L)
Step 6. Partition
Let $ D^{lj=k}_{j=1} $ be a partition of the constraint set $ D $ of problem $ LP_l $. Add problems $ D^{lj=k}_{j=1} $ to L, where $ LP^l_j $ is $ LP_l $ with feasible region restricted to $ D^l_j $ and $ Z_{lj} $ for j=1,...k is set to the value of $ Z^l $ for the parent problem l. Go to step 3.[6]
Numerical Example
First, list out the MILP:
$ min \ z=-4x_1-7x_2 $
$ 6x_1 + x_2 \leq13 $
$ -x_1+4x_2\leq5 $
$ x_1,x_2\geq0 $
Solution to original LP
$ z =-19.56, x_1=1.88, x_2=1.72 $
Branch on x1 to generate sub-problems
$ min \ z=-4x_1-7x_2 $
$ 6x_1 + x_2 \leq13 $
$ -x_1+4x_2\leq5 $
$ x_1\geq2 $
$ x_1,x_2\geq0 $
Solution to fist branch sub-problem
$ z =-15, x_1=2, x_2=1 $
$ min \ z=-4x_1-7x_2 $
$ 6x_1 + x_2 \leq13 $
$ -x_1+4x_2\leq5 $
$ x_1\leq1 $
$ x_1,x_2\geq0 $
Solution to second branch sub-problem
$ z =-14.5, x_1=1, x_2=1.5 $
Adding a cut
$ min \ z=-4x_1-7x_2 $
$ 6x_1 + x_2 \leq13 $
$ -x_1+4x_2\leq5 $
$ 2x_1+x_2\leq 3 $
$ x_1\leq1 $
$ x_1,x_2\geq0 $
Solution to cut LP
$ z=-13.222,x_1=.778,x_2=1.444 $
Application
Several of the Branch and Cut applications are described below in more detail and how they can be used. These applications serve as methods in which Branch and Cut can be used to optimize various problems efficiently.
Combinatorial Optimization
Combinatorial Optimization is a great application for Branch and Cut. This style of optimization is the methodology of utilizing the finite known sets and information of the sets to optimize the solution. The original intent for this application was for maximizing flow as well as in the transportation industry (Maltby and Ross). This combinatorial optimization has also taken on some new areas where it is used often. Combinatorial Optimization is now an imperative component in studying artificial intelligence and machine learning algorithms to optimize solutions. The finite sets that Combinatorial Optimization tends to utilize and focus on includes graphs, partially ordered sets, and structures that define linear independence call matroids.[7]
Bender’s Decomposition
Bender’s Decomposition is another Branch and Cut application that is utilized widely in Stochastic Programming. Bender’s Decomposition is where you take the initial problem and divide into two distinct subsets. By dividing the problem into two separate problems you are able to solve each set easier than the original instance (Benders). Therefore the first problem within the subset created can be solved for the first variable set. The second sub problem is then solved for, given that first problem solution. Doing this allows for the sub problem to be solved to determine whether the first problem is infeasible (Benders). Bender’s cuts can be added to constrain the problem until a feasible solution can be found.[6]
Large-Scale Symmetric Traveling Salesmen Problem
The Large-Scale Symmetric Traveling Salesmen Problem is a common problem that was always looked into optimizing for the shortest route while visiting each city once and returning to the original city at the end. On a larger scale this style of problem must be broken down into subsets or nodes (SIAM). By constraining this style of problem such as the methods of Combinatorial Optimization, the Traveling Salesmen Problem can be viewed as partially ordered sets. By doing this on a large scale with finite cities you are able to optimize the shortest path taken and ensure each city is only visited once.[8]
Submodular Function
Submodular Function is another function in which is used throughout artificial intelligence as well as machine learning. The reason for this is because as inputs are increased into the function the value or outputs decrease. This allows for a great optimization features in the cases stated above because inputs are continually growing. This allows for machine learning and artificial intelligence to continue to grow based on these algorithms (Tschiatschek, Iyer, and Bilmes)[9]. By enforcing new inputs to the system the system will learn more and more to ensure it optimizes the solution that is to be made.[10]
Conclusion
The Branch and Cut is an optimization algorithm used to optimize integer linear programming. It combines two other optimization algorithms - branch and bound and cutting planes in order to utilize the results from each method in order to create the most optimal solution. There are three different methodologies used within the specific method - most infeasible branching, strong branching, and pseudo code. Furthermore, Branch and Cut can be utilized it multiple scenarios - Submodular function, large-scale symmetric traveling salesmen problem, bender's decomposition, and combination optimization which increases the impact of the methodology.
Reference
- ↑ Karamanov, Miroslav. “Branch and Cut: An Empirical Study.” Carnegie Mellon University , Sept. 2006, https://www.cmu.edu/tepper/programs/phd/program/assets/dissertations/2006-operations-research-karamanov-dissertation.pdf.
- ↑ Luedtke, Jim. “The Branch-and-Cut Algorithm for Solving Mixed-Integer Optimization Problems.” Institute for Mathematicians and Its Applications, 10 Aug. 2016, https://www.ima.umn.edu/materials/2015-2016/ND8.1-12.16/25397/Luedtke-mip-bnc-forms.pdf.
- ↑ Branching rules revisited Tobias Achterberga;∗, Thorsten Kocha, Alexander Martinb https://www-m9.ma.tum.de/downloads/felix-klein/20B/AchterbergKochMartin-BranchingRulesRevisited.pdf
- ↑ A Branch-and-Cut Algorithm for Mixed Integer Bilevel Linear Optimization Problems and Its Implementationhttps://coral.ise.lehigh.edu/~ted/files/papers/MIBLP16.pdf
- ↑ Advances in Mixed Integer Programming http://scip.zib.de/download/slides/SCIP-branching.ppt
- ↑ 6.0 6.1 Benders, J. F. (Sept. 1962), "Partitioning procedures for solving mixed-variables programming problems", Numerische Mathematik 4(3): 238–252.
- ↑ Maltby, Henry, and Eli Ross. “Combinatorial Optimization.” Brilliant Math & Science Wiki, https://brilliant.org/wiki/combinatorial-optimization/.
- ↑ Society for Industrial and Applied Mathematics. “SIAM Rev.” SIAM Review, 18 July 2006, https://epubs.siam.org/doi/10.1137/1033004
- ↑ S. Tschiatschek, R. Iyer, H. Wei and J. Bilmes, Learning Mixtures of Submodular Functions for Image Collection Summarization, NIPS-2014.
- ↑ A. Krause and C. Guestrin, Beyond Convexity: Submodularity in Machine Learning, Tutorial at ICML-2008