Column generation algorithms: Difference between revisions
(Updating section I had msised: references) |
No edit summary |
||
| (85 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
Authors: | |||
* Lorena Garcia Fernandez (lgf572) (SysEn 5800 Fall 2020) | |||
* Miguel Hoyos | |||
= | == Introduction <ref>J. Desrosiers, M. L¨ubbecke, G. Desaulniers, J. B. Gauthier (June 2024). Branch-and-Price, Les Cahiers du GERAD G–2024–36, HEC Montr´eal, Canada. Revised version: October 2024</ref> == | ||
Column Generation (CG) is an iterative decomposition method for solving linear problems that typically have a prohibitively large number of variables. The main idea of the algorithm is to remove all variables from the original model and then iteratively reintroduce a limited number of them until it is possible to prove that the smaller problem contains at least one optimal solution to the original problem. The rationale behind this algorithm is that, in an optimal solution, nearly all the variables take the value zero, which means those variables are essentially not part of the model at all. This method simplifies the formulation and resolution of large problems since not all variables need to be explicitly listed to find an optimal solution<ref>Desrosiers, Jacques & Lübbecke, Marco. (2006). A Primer in Column Generation.p7-p14 10.1007/0-387-25486-2_1. </ref>. | |||
CG can be described as the '''primal simplex method''' with a variation on the pricing step. Instead of evaluating the reduced costs of all the variables and selecting the one with the minimum non-positive value (for minimization problems, or the maximum non-negative value for maximization problems), it dynamically generates a new variable that meets that condition (or proves that none exists) by solving an auxiliary optimization problem. | |||
To implement this algorithm the original problem has to be reformulated in a way that the variables (or columns) are described implicitly as the incidence vectors of certain subsets of the set of alternatives (e.g., tours, client subsets)<ref name=":0">Wolsey, L. A. (2021). ''Integer Programming'' (2nd ed.). Wiley. Section 11.4, Solving the Master Problem: Branch-and-Price, pp. 219-222.</ref>, and then decompose it into a Master Problem and at least one Subproblem, also called the Pricing problem. At each iteration, the Subproblem provides a new variable to be included in the Master Problem, which then has to be resolved. This process is repeated until optimality can be proved. | |||
CG is often mentioned in the context of Dantzig-Wolfe decomposition, and some even confuse the two, but they are distinct: the former is an independent method from the latter. | |||
It is important to note that CG can also be applied to solve integer or mixed-integer problems if used to solve the linear relaxation and is implemented within a Branch-and-Bound or Branch-Cut-and-Price algorithm. | |||
== Theory == | |||
Column Generation can be described as a variation of the Simplex Method. Instead of evaluating the reduced costs of all the variables and selecting the one with the minimum value (for minimization problems, maximum for maximization problems), it dynamically generates a new variable by solving an auxiliary optimization problem called the Subproblem or the Pricing Problem. | |||
The way this method work is as follows: | |||
# Formulate the problem in such a way that the columns correspond to incidence vectors of the elements to be decided on on the problem. | |||
# Separate two problems from the original one: the Master Problem (MP) and the Subproblem (SP) or Pricing Problem (PP). | |||
* The master problem is the original column-wise (i.e: one column at a time) formulation of the problem with only a subset of variables being considered.<ref> | |||
AlainChabrier, Column Generation techniques, 2019 URL: https://medium.com/@AlainChabrier/column-generation-techniques-6a414d723a64 | |||
</ref> | |||
* The sub-problem is a new problem created to identify a new promising variable. The objective function of the sub-problem is the reduced cost of the new variable with respect to the current dual variables, and the constraints require that the variable obeys the naturally occurring constraints. The subproblem is also referred to as the RMP or “restricted master problem”. From this we can infer that this method will be a good fit for problems whose constraint set admit a natural breakdown (i.e: decomposition) into sub-systems representing a well understood combinatorial structure.<ref> | |||
AlainChabrier, Column Generation techniques, 2019 URL: https://medium.com/@AlainChabrier/column-generation-techniques-6a414d723a64 | |||
</ref> | |||
To | To execute that decomposition from the original problem into Master and subproblems there are different techniques. The theory behind this method relies on the Dantzig-Wolfe decomposition.<ref>Dantzig-Wolfe decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dantzig-Wolfe_decomposition&oldid=50750</ref> | ||
In summary, when the master problem is solved, we are able to obtain dual prices for each of the constraints in the master problem. This information is then utilized in the objective function of the subproblem. The subproblem is solved. If the objective value of the subproblem is negative, a variable with negative reduced cost has been identified. This variable is then added to the master problem, and the master problem is re-solved. Re-solving the master problem will generate a new set of dual values, and the process is repeated until no negative reduced cost variables are identified. The subproblem returns a solution with non-negative reduced cost, we can conclude that the solution to the master problem is optimal.<ref>Wikipedia, the free encyclopeda. Column Generation. URL: https://en.wikipedia.org/wiki/Column_generation</ref> | |||
== Methodology<ref>L.A. Wolsey, Integer programming. Wiley,Column Generation Algorithms p185-p189,1998</ref> == | |||
[[File:Column Generation.png|thumb|468x468px|Column generation schematics<ref name=":4">GERARD. (2005). Personnel and Vehicle scheduling, Column Generation, slide 12. URL: https://slideplayer.com/slide/6574/</ref>]] | |||
Consider the problem in the form: | |||
A | (IP) | ||
<math>z=max\left \{\sum_{k=1}^{K}c^{k}x^{k}:\sum_{k=1}^{K}A^{k}x^{k}=b,x^{k}\epsilon X^{k}\; \; \; for\; \; \; k=1,...,K \right \}</math> | |||
Where <math>X^{k}=\left \{x^{k}\epsilon Z_{+}^{n_{k}}: D^{k}x^{k}\leq d^{_{k}} \right \}</math> for <math>k=1,...,K</math>. Assuming that each set <math>X^{k}</math> contains a large but finite set of points <math>\left \{ x^{k,t} \right \}_{t=1}^{T_{k}}</math>, we have that <math>X^{k}=</math>: | |||
<math>\left \{ x^{k}\epsilon R^{n_{k}}:x^{k}=\sum_{t=1}^{T_{k}}\lambda _{k,t}x^{k,t},\sum_{t=1}^{T_{k}}\lambda _{k,t}=1,\lambda _{k,t}\epsilon \left \{ 0,1 \right \}for \; \; k=1,...,K \right \}</math> | |||
Note that, on the assumption that each of the sets <math>X^{k}=</math> is bounded for <math>k=1,...,K</math> the approach will involve solving an equivalent problem of the form as below: | |||
<math>max\left \{ \sum_{k=1}^{K}\gamma ^{k}\lambda ^{k}: \sum_{k=1}^{K}B^{k}\lambda ^{k}=\beta ,\lambda ^{k}\geq 0\; \; integer\; \; for\; \; k=1,...,K \right \}</math> | |||
where each matrix <math>B^{k}</math> has a very large number of columns, one for each of the feasible points in <math>X^{k}</math>, and each vector <math>\lambda ^{k}</math> contains the corresponding variables. | |||
Now, substituting for <math>x^{k}=</math> leads to an equivalent ''IP Master Problem (IPM)'': | |||
(IPM) | |||
<math>\begin{matrix} | |||
z=max\sum_{k=1}^{K}\sum_{t=1}^{T_{k}}\left(c^{k}x^{k,t}\right )\lambda _{k,t} \\ \sum_{k=1}^{K}\sum_{t=1}^{T_{k}}\left ( A^{k}x^{k,t} \right )\lambda _{k,t}=b\\ | |||
\sum_{t=1}^{T_{k}}\lambda _{k,t}=1\; \; for\; \; k=1,...,K \\ | |||
\lambda _{k,t}\epsilon \left \{ 0,1 \right \}\; \; for\; \; t=1,...,T_{k}\; \; and\; \; k=1,...,K. | |||
\end{matrix}</math> | |||
To solve the Master Linear Program, we use a column generation algorithm. This is in order to solve the linear programming relaxation of the Integer Programming Master Problem, called the ''Linear Programming Master Problem (LPM)'': | |||
(LPM) | |||
<math>\begin{matrix} | |||
z^{LPM}=max\sum_{k=1}^{K}\sum_{t=1}^{T_{k}}\left ( c^{k}x^{k,t} \right )\lambda _{k,t}\\ | |||
\sum_{k=1}^{K}\sum_{t=1}^{T_{k}}\left ( A^{k}x^{k,t} \right )\lambda _{k,t}=b \\ | |||
\sum_{t=1}^{T_{k}}\lambda _{k,t}=1\; \;for\; \; k=1,...,K \\ | |||
\lambda _{k,t} \geq 0\; \; for\; \; t=1,...,T_{k},\; k=1,...,K | |||
\end{matrix}</math> | |||
Where there is a column <math>\begin{pmatrix} | |||
c^{k}x\\ | |||
A^{k}x\\ | |||
e_{k} | |||
\end{pmatrix}</math> for each ''<math>x</math>'' ''<math display="inline">\in</math> <math display="inline">X^{k}</math>''. On the next steps of this method, we will use <math>\left \{ \pi _{i} \right \}_{i=1}^{m}</math> as the dual variables associated with the joint constraints, and <math>\left \{ \mu_{k} \right \}_{k=1}^{K}</math> as dual variables for the second set of constraints.The latter are also known as convexity constraints. | |||
The idea is to solve the linear program by the primal simplex algorithm. However, the pricing step of choosing a column to enter the basis must be modified because of the very big number of columns in play. Instead of pricing the columns one at a time, the question of finding a column with the biggest reduced price is itself a set of <math>K</math> optimization problems. | |||
''Initialization:'' we suppose that a subset of columns (at least one for each <math>k</math>) is available, providing a feasible ''Restricted Linear Programming Master Problem'': | |||
<math>\begin{matrix} \\ \ | (RLPM) | ||
<math>\begin{matrix} | |||
</math> | z^{LPM}=max\tilde{c}\tilde{\lambda} \\ | ||
\tilde{A}\tilde{\lambda }=b \\ | |||
\tilde{\lambda }\geq 0 | |||
\end{matrix}</math> | |||
where <math>\tilde{b}=\begin{pmatrix} | |||
b\\ | |||
1\\ | |||
\end{pmatrix}</math>, <math>\tilde{A}</math> is generated by the available set of columns and <math>\tilde{c}\tilde{\lambda }</math> are the corresponding costs and variables. Solving the RLPM gives an optimal primal solution <math>\tilde{\lambda ^{*}}</math> and an optimal dual solution <math>\left ( \pi ,\mu \right )\epsilon\; R^{m}\times R^{k}</math> | |||
''Primal feasibility:'' Any feasible solution of ''RLMP'' is feasible for ''LPM''. More precisely, <math>\tilde{\lambda^{*} }</math> is a feasible solution of ''LPM'', and hence <math>\tilde{z}^{LPM}=\tilde{c}\tilde{\lambda ^{*}}=\sum_{i=1}^{m}\pi _{i}b_{i}+\sum_{k=1}^{K}\mu _{k}\leq z^{LPM}</math> | |||
''Optimality check for LPM:'' It is required to check whether <math>\left ( \pi ,\mu \right )</math> is dual feasible for ''LPM''. This means checking for each column, that is for each <math>k</math>, and for each <math>x\; \epsilon \; X^{k}</math> if the reduced price <math>c^{k}x-\pi A^{k}x-\mu _{k}\leq 0</math>. Rather than examining each point separately, we treat all points in <math>X^{k}</math> implicitly, by solving an optimization subproblem: | |||
<math>\zeta _{k}=max\left \{ \left (c^{k}-\pi A^{k} \right )x-\mu _{k}\; :\; x\; \epsilon \; X^{k}\right \}.</math> | |||
''Stopping criteria:'' If <math>\zeta _{k}> 0</math> for <math>k=1,...,K</math> the solution <math>\left ( \pi ,\mu \right )</math> is dual feasible for ''LPM'', and hence <math>z^{LPM}\leq \sum_{i=1}^{m}\pi _{i}b_{i}+\sum_{k=1}^{K}\mu _{k}</math>. As the value of the primal feasible solution <math>\tilde{\lambda }</math> equals that of this upper bound, <math>\tilde{\lambda }</math> is optimal for ''LPM''. | |||
As | |||
<math>\begin{ | ''Generating a new column:'' If <math>\zeta _{k}> 0</math> for some <math>k</math>, the column corresponding to the optimal solution <math>\tilde{x}^{k}</math> of the subproblem has a positive reduced price. Introducing the column <math>\begin{pmatrix} | ||
c^{k}x\\ | |||
</math> | A^{k}x\\ | ||
e_{k} | |||
\end{pmatrix}</math> leads then to a Restricted Linear Programming Master Problem that can be easily reoptimized (e.g., by the primal simplex algorithm) | |||
== Numerical example: The one-dimensional Cutting Stock problem<ref>L.A. Wolsey, Integer programming. Wiley,Column Generation Algorithms p185-p189,1998The Cutting Stock problem</ref> == | |||
=== Problem Overview === | |||
A company produces steel bars with a diameter of 45 millimeters and a length of 33 meters. The company also handles cutting the bars to meet the specific length requirements of its customers. Currently, the following demand forecast is expected and must be satisfied: | |||
= | |||
A company produces steel bars with diameter 45 millimeters and length 33 meters. The company also | |||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+ | ||
|Pieces needed | |'''Pieces needed''' | ||
|Piece length(m) | |'''Piece length(m)''' | ||
|Type of item | |'''Type of item''' | ||
|- | |- | ||
|144 | |144 | ||
| Line 150: | Line 142: | ||
|5 | |5 | ||
|} | |} | ||
The objective is to | The objective is to determine the minimum number of steel bars required to satisfy the total demand. | ||
A possible model for | A possible model for this problem, proposed by Gilmore and Gomory in the 1960s, is as follows: | ||
'''Sets''' | '''Sets''' | ||
K = {1, 2, 3, 4, 5}: set of item types; | <math>K=\left \{ 1,2,3,4,5 \right \}</math>: set of item types; | ||
S: set of patterns (i.e., possible ways) that can be | ''<math display="inline">S</math>:'' set of patterns (i.e., possible ways) that can be used to cut a given bar into portions of the required lengths. It is important to note that the cardinality of this set is unknown a priori and can be extremely large. | ||
'''Parameters''' | '''Parameters''' | ||
M: bar length (before the cutting process) | <math display="inline">M</math>: bar length (before the cutting process); | ||
<math display="inline">L_k</math>'':'' length of item ''<math display="inline">k</math>'' ''<math display="inline">\in</math> <math display="inline">K</math>''; | |||
<math display="inline">R_s</math> : number of pieces of type ''<math display="inline">k</math>'' ''<math display="inline">\in</math> <math display="inline">K</math>'' required; | |||
<math display="inline">N_{ks}</math> : number of pieces of type ''<math display="inline">k</math>'' ''<math display="inline">\in</math> <math display="inline">K</math>'' in pattern ''<math display="inline">s</math>'' ''<math display="inline">\in</math> <math display="inline">S</math>''. | |||
'''Decision variables''' | '''Decision variables''' | ||
<math display="inline">y_s</math> : number of bars that should be portioned using pattern ''<math display="inline">s</math>'' ''<math display="inline">\in</math> <math display="inline">S</math>''. | |||
'''Model''' | '''Model''' | ||
<math>\begin{ | <math>\begin{align}\min&\sum_{s=1}^Sy_s\\ | ||
s.t.&\\ | |||
& \sum_sN_{ks}y_s\geq R_k & \forall k\in K \\ | |||
& y_s\in \Zeta_+ & \forall s\in S \\ | |||
\end{align} | |||
</math> | </math> | ||
=== Solving the problem === | |||
To directly solve the model, it is necessary to know all the parameters, in particular <math display="inline">N_{ks}</math>. This means we need to be able to enumerate all the elements in set <math>S | |||
</math> and determine hoy many pieces of each item are present. The problem lies in the fact that the cardinality of <math>S | |||
</math> (i.e. the number of elements in the set) is extremely large, making the direct solve an impractical task. | |||
Another issue with the formulation presented above is that the <math display="inline">y_{s}</math> variables are integer. As stated in <ref>Gilmore, P. C., & Gomory, R. E. (1961). A Linear Programming Approach to the Cutting-Stock Problem. ''Operations Research, 9''(6), 849-859. INFORMS.</ref>, we can relax this constraint, which will result in a non-integer solution most of the time. We can then either round up, resulting in a higher cost, or round down, leaving some demand unmet, which would require the use of ad hoc methods. The authors also note that if the non-integer values are high, any rounding will produce only a marginal change in the cost (here, the cost is equivalent to the number of bars). The common practice is to use the relaxed solution as a starting point for a branch-and-bound algorithm, possibly combined with cutting planes<ref name=":0" />.<blockquote><u>''Key take-away: In the next steps of this example we will analyze how to solve the continuous relaxation of the model.''</u></blockquote> | |||
==== Restricted Master Problem ==== | |||
As a starting point, we need any feasible solution. Such a solution can be constructed as follows: | |||
# We consider any single-item cutting patterns, i.e., <math>\|K\| | |||
</math> configurations, each containing <math display="inline">{\textstyle N_{ks} } = \lfloor \frac{W}{L_k}\rfloor | |||
</math> pieces of type <math>k | |||
</math> | |||
# Set <math display="inline">{\textstyle y_{k}} = \llcorner \frac{R_s}{N_{k,s}}\lrcorner | |||
</math> for pattern <math>k | |||
</math> (where pattern <math>k | |||
</math> is the pattern containing only pieces of type <math>k | |||
</math>). | |||
This solution could also be arrived to by applying the simplex method to the model (without integrality constraints), considering only the decision variables that correspond to the above single-item patterns: | |||
<math>\begin{align} | |||
\text{min} & ~~ y_{1}+y_{2}+y_{3}+y_{4}+y_{5}\\ | |||
\text{s.t} & ~~ 15y_{1} \ge 144\\ | |||
\ & ~~ 6y_{2} \ge 105\\ | |||
\ & ~~ 6y_{3} \ge 72\\ | |||
\ & ~~ 6y_{4} \ge 30\\ | |||
\ & ~~ 3y_{5} \ge 24\\ | |||
\ & ~~ y_{1},y_{2},y_{3},y_{4},y_{5} \ge 0\\ | |||
\end{align}</math> | |||
In fact, if we solve this problem (for example, use CPLEX solver in GAMS) the solution is as below : | In fact, if we solve this problem (for example, use CPLEX solver in GAMS) the solution is as below: | ||
{| class="wikitable" | {| class="wikitable" | ||
|Y1 | |Y1 | ||
| Line 218: | Line 235: | ||
|24 | |24 | ||
|} | |} | ||
Next, a new possible pattern (number 6) will be | Next, a new possible pattern (number <math>6</math>) will be considered. This pattern contains only one piece of item type number <math>5</math>. So the question is if the new solution would remain optimal if this new pattern was allowed. Duality helps answer ths question. At every iteration of the simplex method, the outcome is a feasible basic solution (corresponding to some basis <math>B</math>) for the primal problem and a dual solution (the multipliers <math>u^{t}=c^{t}BB^{-1}</math>) that satisfy the complementary slackness conditions. (Note: the dual solution will be feasible only when the last iteration is reached) | ||
The inclusion of new pattern | The inclusion of new pattern <math>6</math> corresponds to including a new variable in the primal problem, with objective cost <math>1</math> (as each time pattern <math>6</math> is chosen, one bar is cut) and corresponding to the following column in the constraint matrix: | ||
<math>D_6= \begin{bmatrix} | <math>D_6= \begin{bmatrix} | ||
| Line 228: | Line 245: | ||
\ 0 \\ | \ 0 \\ | ||
\ 1 \\ | \ 1 \\ | ||
\end{bmatrix} | \end{bmatrix}</math> | ||
These variables create a new dual constraint. We then have to check if this new constraint is violated by the current dual solution ( or in other words, ''if the reduced cost of the new variable with respect to basis B is negative)'' | These variables create a new dual constraint. We then have to check if this new constraint is violated by the current dual solution (or in other words, ''if the reduced cost of the new variable with respect to basis <math>B</math> is negative)'' | ||
The new dual constraint is: | The new dual constraint is:<math>1\times u_{1}+0\times u_{2}+0\times u_{3}+0\times u_{4}+1\times u_{5}\leq 1</math> | ||
The solution for the dual problem can be computed in different software packages, or by hand. The example below shows the solution obtained with GAMS for this example: | |||
(Note the solution for the dual problem would be: <math>u=c_{T}^{B}B^{-1}</math>) | |||
{| class="wikitable" | {| class="wikitable" | ||
|Dual variable | |Dual variable | ||
| Line 264: | Line 276: | ||
|0.333 | |0.333 | ||
|} | |} | ||
Since 0.2+1 = 1.2 > 1, the new constraint is violated. | Since <math>0.2+1=1.2> 1</math>, the new constraint is violated. | ||
This means that the current primal solution (in which the new variable is | This means that the current primal solution (in which the new variable is <math>y_{6}=0</math>) may not be optimal anymore (although it is still feasible). The fact that the dual constraint is violated means the associated primal variable has negative reduced cost: | ||
the norm of | the norm of <math>c_6 = c_6-u^TD_6=1-0.4=0.6</math> | ||
< | To help us solve the problem, the next step is to let <math>y_{6}</math> enter the basis. To do so, we modify the problem by inserting the new variable as below: | ||
<math>\begin{align} | |||
\text{min} & ~~ y_{1}+y_{2}+y_{3}+y_{4}+y_{5}+y_{6}\\ | |||
\text{s.t} & ~~ 15y_{1} +y_{6}\ge 144\\ | |||
\ & ~~ 6y_{2} \ge 105\\ | |||
\ & ~~ 6y_{3} \ge 72\\ | |||
\ & ~~ 6y_{4} \ge 30\\ | |||
\ & ~~ 3y_{5}+y_{6} \ge 24\\ | |||
\ & ~~ y_{1},y_{2},y_{3},y_{4},y_{5},y_{6} \ge 0\\ | |||
\end{align}</math> | |||
If this problem is solved with the simplex method, the optimal solution is found, but restricted only to patterns <math>1</math> to <math>6</math>. If a new pattern is available, a decision should be made whether this new pattern should be used or not by proceeding as above. However, the problem is how to find a pattern (i.e., a variable; i.e, a column of the matrix) whose reduced cost is negative (i.e., which will mean it is convenient to include it in the formulation). At this point one can notice that number of possible patterns exponentially large,and all the patterns are not even known explicitly. The question then is: | |||
If this problem is solved with the simplex method, the optimal solution is found, but restricted only to patterns 1 to 6. If a new pattern is available, a decision should be made whether this new pattern should be used or not by proceeding as above. However, the problem is how to find a pattern (i.e., a variable; i.e, a column of the matrix) whose reduced cost is negative (i.e., which will mean it is convenient to include it in the formulation). At this point one can notice that number of possible patterns exponentially large,and all the patterns are not even known explicitly. The question then is: | |||
''Given a basic optimal solution for the problem in which only some variables are included, how can we find (if any exists) a variable with negative reduced cost (i.e., a constraint violated by the current dual solution)?'' | ''Given a basic optimal solution for the problem in which only some variables are included, how can we find (if any exists) a variable with negative reduced cost (i.e., a constraint violated by the current dual solution)?'' | ||
| Line 292: | Line 301: | ||
This question can be transformed into an optimization problem: in order to see whether a variable with negative reduced cost exists, we can look for the minimum of the reduced costs of all possible variables and check whether this minimum is negative: | This question can be transformed into an optimization problem: in order to see whether a variable with negative reduced cost exists, we can look for the minimum of the reduced costs of all possible variables and check whether this minimum is negative: | ||
c | <math>\bar{c}=1-u^Tz</math> | ||
Because every column of the constraint matrix corresponds to a cutting pattern, and every entry of the column says how many pieces of a certain type are in that pattern. In order for z to be a possible column of the constraint matrix, the following condition must be satisfied: | Because every column of the constraint matrix corresponds to a cutting pattern, and every entry of the column says how many pieces of a certain type are in that pattern. In order for <math>z | ||
</math> to be a possible column of the constraint matrix, the following condition must be satisfied: | |||
<math>\begin{matrix} | <math display="inline">\begin{matrix}z_k\in \Zeta_+\forall k\in K \\ \ \sum_kL_kz_k \leq M \end{matrix} | ||
</math> | </math> | ||
And by so | And by so doing, it enables the conversion of the problem of finding a variable with negative reduced cost into the integer linear programming problem below: | ||
<math>\begin{matrix} | <math>\begin{matrix}\min\ \bar{c} = 1 - sum_{k=1}^K u_k \times z_k \\ \ s.t. \sum_kL_kz_k \leq M \\ z_k\in \Zeta_+\forall k\in K \end{matrix} | ||
</math> | </math> | ||
which, in turn, would be equivalent to the below formulation (we just write the objective in maximization form and ignore the additive constant 1): | which, in turn, would be equivalent to the below formulation (we just write the objective in maximization form and ignore the additive constant <math>1</math>): | ||
<math>\begin{matrix} | <math>\begin{matrix} \max\sum_{k=1}^K u_k \times z_k \\ \ s.t. \sum_kL_kz_k \leq M \\ z_k\in \Zeta_+\forall k\in K \end{matrix}</math> | ||
The coefficients | The coefficients <math>z_k | ||
</math> of a column with negative reduced cost can be found by solving the above integer [[wikipedia:Knapsack_problem|"knapsack"]] problem (which is a traditional type of problem that we find in integer programming). | |||
In our example, if we start from the problem restricted to the five single-item patterns, the above problem reads as: | In our example, if we start from the problem restricted to the five single-item patterns, the above problem reads as: | ||
<math>\begin{align} | |||
\text{min} & ~~ 0.067z_{1}+0.167z_{2}+0.167z_{3}+0.167z_{4}+z_{5}\\ | |||
\text{s.t} & ~~ 6z_{1} +13.5z_{2}+15z_{3}+16.5z_{4}+22.5z_{5}\le 33\\ | |||
\ & ~~ z_{1},z_{2},z_{3},z_{4},z_{5}\ge 0\\ | |||
\end{align}</math> | |||
which has the following optimal solution: <math>z^T= [1 \quad 0\quad 0\quad 0\quad 1]</math> | |||
This matches the pattern we called <math>D6</math>, earlier on in this page. | |||
<u>Optimality test</u> | |||
< | If : <math display="inline">\sum_{k=1}^{K}z_{k}^{*}u_{k}^{*}\leq 1</math> | ||
then <math>y^*</math> is an optimal solution of the full continuous relaxed problem (that is, including all patterns in ''<math display="inline">S</math>'') | |||
<math>\ | If this condition is not true, we go ahead and update the master problem by including in ''<math display="inline">S^'</math>'' the pattern <math>\lambda</math> defined by <math>N_{s,\lambda}</math> (in practical terms this means that the column '''<math>y^*</math>''' needs to be included in the constraint matrix) | ||
</math> | |||
For this example we find that the optimality test is met as <math>\sum_{k=1}^{K}z_{k}^{*}u_{k}^{*}=0.4 \leq 1</math> so we have have found an optimal solution of the relaxed continuous problem (if this was not the case we would have had to go back to reformulating and solving the master problem, as discussed in the methodology section of this page) | |||
'''''Algorithm discussion''''' | '''''Algorithm discussion''''' | ||
The column generation subproblem is the critical part of the method is | The column generation subproblem is the critical part of the method is generating the new columns. It is not reasonable to compute the reduced costs of all variables <math>y_s | ||
</math> for <math>s=1,...,S</math>, otherwise this procedure would reduce to the simplex method. In fact, n<math>n</math> can be very large (as in the cutting-stock problem) or, for some reason, it might not be possible or convenient to enumerate all decision variables. This is when it would be necessary to study a specific column generation algorithm for each problem; ''only if such an algorithm exists (and is practical)'', the method can be fully applied. In the one-dimensional cutting stock problem, we transformed the column generation subproblem into an easily solvable integer linear programming problem. In other cases, the computational effort required to solve the subproblem is too high, such that appying this full procedure becomes unefficient. | |||
= | == Applications == | ||
As previously mentioned, column generation techniques are most relevant when the problem that we are trying to solve has a high ratio of number of variables with respect to the number of constraints. As such some common applications are: | As previously mentioned, column generation techniques are most relevant when the problem that we are trying to solve has a high ratio of number of variables with respect to the number of constraints. As such some common applications are: | ||
* Bandwith packing | |||
* Bus driver scheduling | |||
* Generally, column generation algorithms are used for large delivery networks, often in combination with other methods, helping to implement real-time solutions for on-demand logistics. We discuss a supply chain scheduling application below. | |||
=== '''''Bandwidth packing''''' === | |||
The objective of this problem is to allocate bandwidth in a telecommunications network to maximize total revenue. The routing of a set of traffic demands between different users is to be decided, taking into account the capacity of the network arcs and the fact that the traffic between each pair of users cannot be split The problem can be formulated as an integer programming problem and the linear programming relaxation solved using column generation and the simplex algorithm. A branch and bound procedure which branches upon a particular path is used in this particular paper<ref name=":3">Parker, Mark & Ryan, Jennifer. (1993). A column generation algorithm for bandwidth packing. Telecommunication Systems. 2. 185-195. 10.1007/BF02109857. </ref> that looks into bandwidth routing, to solve the IP. The column generation algorithm greatly reduces the complexity of this problem. | |||
=== '''''Bus driver scheduling''''' === | |||
Bus driver scheduling aims to find the minimum number of bus drivers to cover a published timetable of a bus company. When scheduling bus drivers, contractual working rules must be enforced, thus complicating the problem. A column generation algorithm can decompose this complicated problem into a master problem and a series of pricing subproblems. The master problem would select optimal duties from a set of known feasible duties, and the pricing subproblem would augment the feasible duty set to improve the solution obtained in the master problem.<ref name=":2">Dung‐Ying Lin, Ching‐Lan Hsu. Journal of Advanced Transportation. Volume50, Issue8, December 2016, Pages 1598-1615. URL: https://onlinelibrary.wiley.com/doi/abs/10.1002/atr.1417</ref> | |||
=== '''''Supply Chain scheduling problem''''' === | |||
A typical application is where we consider the problem of scheduling a set of shipments between different nodes of a supply chain network. Each shipment has a fixed departure time, as well as an origin and a destination node, which, combined, determine the duration of the associated trip. The aim is to schedule as many shipments as possible, while also minimizing the number of vehicles utilized for this purpose. This problem can be formulated by an integer programming model and an associated branch and price solution algorithm. The optimal solution to the LP relaxation of the problem can be obtained through column generation, solving the linear program a huge number of variables, without explicitly considering all of them. In the context of this application, the master problem schedules the maximum possible number of shipments using only a small set of vehicle-routes, and a column generation (colgen) sub-problem would generate cost-effective vehicle-routes to be fed fed into the master problem. After finding the optimal solution to the LP relaxation of the problem, the algorithm would branch on the fractional decision variables (vehicle-routes), in order to reach the optimal integer solution.<ref name=":1">Kozanidis, George. (2014). Column generation for scheduling shipments within a supply chain network with the minimum number of vehicles. OPT-i 2014 - 1st International Conference on Engineering and Applied Sciences Optimization, Proceedings. 888-898</ref> | |||
== Conclusions == | |||
Column generation is a way of starting with a small, manageable part of a problem (specifically, with some of the variables), solving that part, analyzing that interim solution to find the next part of the problem (specifically, one or more variables) to add to the model, and then solving the full or extended model. In the column generation method, the algorithm steps are repeated until an optimal solution to the entire problem is achieved.<ref> ILOG CPLEX 11.0 User's Manual > Discrete Optimization > Using Column Generation: a Cutting Stock Example > What Is Column Generation? 1997-2007. URL:http://www-eio.upc.es/lceio/manuals/cplex-11/html/usrcplex/usingColumnGen2.html#:~:text=In%20formal%20terms%2C%20column%20generation,method%20of%20solving%20the%20problem.&text=By%201960%2C%20Dantzig%20and%20Wolfe,problems%20with%20a%20decomposable%20structure</ref> | |||
This algorithm provides a way of solving a linear programming problem adding columns (corresponding to constrained variables) during the pricing phase of the problem solving phase, that would otherwise be very tedious to formulate and compute. Generating a column in the primal formulation of a linear programming problem corresponds to adding a constraint in its dual formulation. | |||
== References == | |||
Latest revision as of 13:55, 16 January 2025
Authors:
- Lorena Garcia Fernandez (lgf572) (SysEn 5800 Fall 2020)
- Miguel Hoyos
Introduction [1]
Column Generation (CG) is an iterative decomposition method for solving linear problems that typically have a prohibitively large number of variables. The main idea of the algorithm is to remove all variables from the original model and then iteratively reintroduce a limited number of them until it is possible to prove that the smaller problem contains at least one optimal solution to the original problem. The rationale behind this algorithm is that, in an optimal solution, nearly all the variables take the value zero, which means those variables are essentially not part of the model at all. This method simplifies the formulation and resolution of large problems since not all variables need to be explicitly listed to find an optimal solution[2].
CG can be described as the primal simplex method with a variation on the pricing step. Instead of evaluating the reduced costs of all the variables and selecting the one with the minimum non-positive value (for minimization problems, or the maximum non-negative value for maximization problems), it dynamically generates a new variable that meets that condition (or proves that none exists) by solving an auxiliary optimization problem.
To implement this algorithm the original problem has to be reformulated in a way that the variables (or columns) are described implicitly as the incidence vectors of certain subsets of the set of alternatives (e.g., tours, client subsets)[3], and then decompose it into a Master Problem and at least one Subproblem, also called the Pricing problem. At each iteration, the Subproblem provides a new variable to be included in the Master Problem, which then has to be resolved. This process is repeated until optimality can be proved.
CG is often mentioned in the context of Dantzig-Wolfe decomposition, and some even confuse the two, but they are distinct: the former is an independent method from the latter.
It is important to note that CG can also be applied to solve integer or mixed-integer problems if used to solve the linear relaxation and is implemented within a Branch-and-Bound or Branch-Cut-and-Price algorithm.
Theory
Column Generation can be described as a variation of the Simplex Method. Instead of evaluating the reduced costs of all the variables and selecting the one with the minimum value (for minimization problems, maximum for maximization problems), it dynamically generates a new variable by solving an auxiliary optimization problem called the Subproblem or the Pricing Problem.
The way this method work is as follows:
- Formulate the problem in such a way that the columns correspond to incidence vectors of the elements to be decided on on the problem.
- Separate two problems from the original one: the Master Problem (MP) and the Subproblem (SP) or Pricing Problem (PP).
- The master problem is the original column-wise (i.e: one column at a time) formulation of the problem with only a subset of variables being considered.[4]
- The sub-problem is a new problem created to identify a new promising variable. The objective function of the sub-problem is the reduced cost of the new variable with respect to the current dual variables, and the constraints require that the variable obeys the naturally occurring constraints. The subproblem is also referred to as the RMP or “restricted master problem”. From this we can infer that this method will be a good fit for problems whose constraint set admit a natural breakdown (i.e: decomposition) into sub-systems representing a well understood combinatorial structure.[5]
To execute that decomposition from the original problem into Master and subproblems there are different techniques. The theory behind this method relies on the Dantzig-Wolfe decomposition.[6]
In summary, when the master problem is solved, we are able to obtain dual prices for each of the constraints in the master problem. This information is then utilized in the objective function of the subproblem. The subproblem is solved. If the objective value of the subproblem is negative, a variable with negative reduced cost has been identified. This variable is then added to the master problem, and the master problem is re-solved. Re-solving the master problem will generate a new set of dual values, and the process is repeated until no negative reduced cost variables are identified. The subproblem returns a solution with non-negative reduced cost, we can conclude that the solution to the master problem is optimal.[7]
Methodology[8]
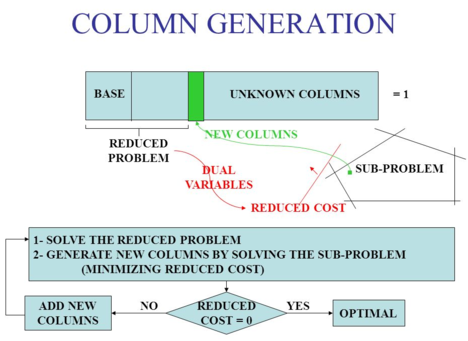
Consider the problem in the form:
(IP) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=max\left \{\sum_{k=1}^{K}c^{k}x^{k}:\sum_{k=1}^{K}A^{k}x^{k}=b,x^{k}\epsilon X^{k}\; \; \; for\; \; \; k=1,...,K \right \}}
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X^{k}=\left \{x^{k}\epsilon Z_{+}^{n_{k}}: D^{k}x^{k}\leq d^{_{k}} \right \}}
for . Assuming that each set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X^{k}}
contains a large but finite set of points Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \{ x^{k,t} \right \}_{t=1}^{T_{k}}}
, we have that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X^{k}=}
:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \{ x^{k}\epsilon R^{n_{k}}:x^{k}=\sum_{t=1}^{T_{k}}\lambda _{k,t}x^{k,t},\sum_{t=1}^{T_{k}}\lambda _{k,t}=1,\lambda _{k,t}\epsilon \left \{ 0,1 \right \}for \; \; k=1,...,K \right \}}
Note that, on the assumption that each of the sets Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X^{k}=} is bounded for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k=1,...,K} the approach will involve solving an equivalent problem of the form as below:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle max\left \{ \sum_{k=1}^{K}\gamma ^{k}\lambda ^{k}: \sum_{k=1}^{K}B^{k}\lambda ^{k}=\beta ,\lambda ^{k}\geq 0\; \; integer\; \; for\; \; k=1,...,K \right \}}
where each matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B^{k}} has a very large number of columns, one for each of the feasible points in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X^{k}} , and each vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda ^{k}} contains the corresponding variables.
Now, substituting for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^{k}=}
leads to an equivalent IP Master Problem (IPM):
(IPM) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix} z=max\sum_{k=1}^{K}\sum_{t=1}^{T_{k}}\left(c^{k}x^{k,t}\right )\lambda _{k,t} \\ \sum_{k=1}^{K}\sum_{t=1}^{T_{k}}\left ( A^{k}x^{k,t} \right )\lambda _{k,t}=b\\ \sum_{t=1}^{T_{k}}\lambda _{k,t}=1\; \; for\; \; k=1,...,K \\ \lambda _{k,t}\epsilon \left \{ 0,1 \right \}\; \; for\; \; t=1,...,T_{k}\; \; and\; \; k=1,...,K. \end{matrix}}
To solve the Master Linear Program, we use a column generation algorithm. This is in order to solve the linear programming relaxation of the Integer Programming Master Problem, called the Linear Programming Master Problem (LPM):
(LPM) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix} z^{LPM}=max\sum_{k=1}^{K}\sum_{t=1}^{T_{k}}\left ( c^{k}x^{k,t} \right )\lambda _{k,t}\\ \sum_{k=1}^{K}\sum_{t=1}^{T_{k}}\left ( A^{k}x^{k,t} \right )\lambda _{k,t}=b \\ \sum_{t=1}^{T_{k}}\lambda _{k,t}=1\; \;for\; \; k=1,...,K \\ \lambda _{k,t} \geq 0\; \; for\; \; t=1,...,T_{k},\; k=1,...,K \end{matrix}}
Where there is a column Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} c^{k}x\\ A^{k}x\\ e_{k} \end{pmatrix}} for each Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle \in} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle X^{k}} . On the next steps of this method, we will use Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \{ \pi _{i} \right \}_{i=1}^{m}} as the dual variables associated with the joint constraints, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \{ \mu_{k} \right \}_{k=1}^{K}} as dual variables for the second set of constraints.The latter are also known as convexity constraints. The idea is to solve the linear program by the primal simplex algorithm. However, the pricing step of choosing a column to enter the basis must be modified because of the very big number of columns in play. Instead of pricing the columns one at a time, the question of finding a column with the biggest reduced price is itself a set of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K} optimization problems.
Initialization: we suppose that a subset of columns (at least one for each Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k}
) is available, providing a feasible Restricted Linear Programming Master Problem:
(RLPM) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix} z^{LPM}=max\tilde{c}\tilde{\lambda} \\ \tilde{A}\tilde{\lambda }=b \\ \tilde{\lambda }\geq 0 \end{matrix}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{b}=\begin{pmatrix} b\\ 1\\ \end{pmatrix}}
, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{A}}
is generated by the available set of columns and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{c}\tilde{\lambda }}
are the corresponding costs and variables. Solving the RLPM gives an optimal primal solution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{\lambda ^{*}}}
and an optimal dual solution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left ( \pi ,\mu \right )\epsilon\; R^{m}\times R^{k}}
Primal feasibility: Any feasible solution of RLMP is feasible for LPM. More precisely, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{\lambda^{*} }}
is a feasible solution of LPM, and hence Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{z}^{LPM}=\tilde{c}\tilde{\lambda ^{*}}=\sum_{i=1}^{m}\pi _{i}b_{i}+\sum_{k=1}^{K}\mu _{k}\leq z^{LPM}}
Optimality check for LPM: It is required to check whether Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left ( \pi ,\mu \right )} is dual feasible for LPM. This means checking for each column, that is for each Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} , and for each Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\; \epsilon \; X^{k}} if the reduced price Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c^{k}x-\pi A^{k}x-\mu _{k}\leq 0} . Rather than examining each point separately, we treat all points in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X^{k}} implicitly, by solving an optimization subproblem:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \zeta _{k}=max\left \{ \left (c^{k}-\pi A^{k} \right )x-\mu _{k}\; :\; x\; \epsilon \; X^{k}\right \}.}
Stopping criteria: If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \zeta _{k}> 0}
for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k=1,...,K}
the solution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left ( \pi ,\mu \right )}
is dual feasible for LPM, and hence Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z^{LPM}\leq \sum_{i=1}^{m}\pi _{i}b_{i}+\sum_{k=1}^{K}\mu _{k}}
. As the value of the primal feasible solution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{\lambda }}
equals that of this upper bound, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{\lambda }}
is optimal for LPM.
Generating a new column: If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \zeta _{k}> 0}
for some Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k}
, the column corresponding to the optimal solution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{x}^{k}}
of the subproblem has a positive reduced price. Introducing the column Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} c^{k}x\\ A^{k}x\\ e_{k} \end{pmatrix}}
leads then to a Restricted Linear Programming Master Problem that can be easily reoptimized (e.g., by the primal simplex algorithm)
Numerical example: The one-dimensional Cutting Stock problem[10]
Problem Overview
A company produces steel bars with a diameter of 45 millimeters and a length of 33 meters. The company also handles cutting the bars to meet the specific length requirements of its customers. Currently, the following demand forecast is expected and must be satisfied:
| Pieces needed | Piece length(m) | Type of item |
| 144 | 6 | 1 |
| 105 | 13.5 | 2 |
| 72 | 15 | 3 |
| 30 | 16.5 | 4 |
| 24 | 22.5 | 5 |
The objective is to determine the minimum number of steel bars required to satisfy the total demand.
A possible model for this problem, proposed by Gilmore and Gomory in the 1960s, is as follows:
Sets
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K=\left \{ 1,2,3,4,5 \right \}} : set of item types;
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle S} : set of patterns (i.e., possible ways) that can be used to cut a given bar into portions of the required lengths. It is important to note that the cardinality of this set is unknown a priori and can be extremely large.
Parameters
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle M} : bar length (before the cutting process);
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle L_k} : length of item Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle k} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle \in} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle K} ;
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle R_s} : number of pieces of type Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle k} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle \in} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle K} required;
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle N_{ks}} : number of pieces of type Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle k} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle \in} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle K} in pattern Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle s} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle \in} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle S} .
Decision variables
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle y_s} : number of bars that should be portioned using pattern Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle s} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle \in} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle S} .
Model
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}\min&\sum_{s=1}^Sy_s\\ s.t.&\\ & \sum_sN_{ks}y_s\geq R_k & \forall k\in K \\ & y_s\in \Zeta_+ & \forall s\in S \\ \end{align} }
Solving the problem
To directly solve the model, it is necessary to know all the parameters, in particular Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle N_{ks}} . This means we need to be able to enumerate all the elements in set and determine hoy many pieces of each item are present. The problem lies in the fact that the cardinality of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S } (i.e. the number of elements in the set) is extremely large, making the direct solve an impractical task.
Another issue with the formulation presented above is that the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle y_{s}} variables are integer. As stated in [11], we can relax this constraint, which will result in a non-integer solution most of the time. We can then either round up, resulting in a higher cost, or round down, leaving some demand unmet, which would require the use of ad hoc methods. The authors also note that if the non-integer values are high, any rounding will produce only a marginal change in the cost (here, the cost is equivalent to the number of bars). The common practice is to use the relaxed solution as a starting point for a branch-and-bound algorithm, possibly combined with cutting planes[3].
Key take-away: In the next steps of this example we will analyze how to solve the continuous relaxation of the model.
Restricted Master Problem
As a starting point, we need any feasible solution. Such a solution can be constructed as follows:
- We consider any single-item cutting patterns, i.e., Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \|K\| } configurations, each containing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle {\textstyle N_{ks} } = \lfloor \frac{W}{L_k}\rfloor } pieces of type Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k }
- Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle {\textstyle y_{k}} = \llcorner \frac{R_s}{N_{k,s}}\lrcorner } for pattern Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k } (where pattern Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k } is the pattern containing only pieces of type Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k } ).
This solution could also be arrived to by applying the simplex method to the model (without integrality constraints), considering only the decision variables that correspond to the above single-item patterns:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \text{min} & ~~ y_{1}+y_{2}+y_{3}+y_{4}+y_{5}\\ \text{s.t} & ~~ 15y_{1} \ge 144\\ \ & ~~ 6y_{2} \ge 105\\ \ & ~~ 6y_{3} \ge 72\\ \ & ~~ 6y_{4} \ge 30\\ \ & ~~ 3y_{5} \ge 24\\ \ & ~~ y_{1},y_{2},y_{3},y_{4},y_{5} \ge 0\\ \end{align}}
In fact, if we solve this problem (for example, use CPLEX solver in GAMS) the solution is as below:
| Y1 | 28.8 |
| Y2 | 52.5 |
| Y3 | 24 |
| Y4 | 15 |
| Y5 | 24 |
Next, a new possible pattern (number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6} ) will be considered. This pattern contains only one piece of item type number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5} . So the question is if the new solution would remain optimal if this new pattern was allowed. Duality helps answer ths question. At every iteration of the simplex method, the outcome is a feasible basic solution (corresponding to some basis Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} ) for the primal problem and a dual solution (the multipliers Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u^{t}=c^{t}BB^{-1}} ) that satisfy the complementary slackness conditions. (Note: the dual solution will be feasible only when the last iteration is reached)
The inclusion of new pattern Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6} corresponds to including a new variable in the primal problem, with objective cost Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} (as each time pattern Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6} is chosen, one bar is cut) and corresponding to the following column in the constraint matrix:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_6= \begin{bmatrix} \ 1 \\ \ 0 \\ \ 0 \\ \ 0 \\ \ 1 \\ \end{bmatrix}}
These variables create a new dual constraint. We then have to check if this new constraint is violated by the current dual solution (or in other words, if the reduced cost of the new variable with respect to basis Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B}
is negative)
The new dual constraint is:Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1\times u_{1}+0\times u_{2}+0\times u_{3}+0\times u_{4}+1\times u_{5}\leq 1}
The solution for the dual problem can be computed in different software packages, or by hand. The example below shows the solution obtained with GAMS for this example:
(Note the solution for the dual problem would be: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u=c_{T}^{B}B^{-1}} )
| Dual variable | Variable value |
| D1 | 0.067 |
| D2 | 0.167 |
| D3 | 0.167 |
| D4 | 0.167 |
| D5 | 0.333 |
Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0.2+1=1.2> 1} , the new constraint is violated.
This means that the current primal solution (in which the new variable is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{6}=0} ) may not be optimal anymore (although it is still feasible). The fact that the dual constraint is violated means the associated primal variable has negative reduced cost:
the norm of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_6 = c_6-u^TD_6=1-0.4=0.6}
To help us solve the problem, the next step is to let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{6}} enter the basis. To do so, we modify the problem by inserting the new variable as below:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \text{min} & ~~ y_{1}+y_{2}+y_{3}+y_{4}+y_{5}+y_{6}\\ \text{s.t} & ~~ 15y_{1} +y_{6}\ge 144\\ \ & ~~ 6y_{2} \ge 105\\ \ & ~~ 6y_{3} \ge 72\\ \ & ~~ 6y_{4} \ge 30\\ \ & ~~ 3y_{5}+y_{6} \ge 24\\ \ & ~~ y_{1},y_{2},y_{3},y_{4},y_{5},y_{6} \ge 0\\ \end{align}}
If this problem is solved with the simplex method, the optimal solution is found, but restricted only to patterns Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1}
to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6}
. If a new pattern is available, a decision should be made whether this new pattern should be used or not by proceeding as above. However, the problem is how to find a pattern (i.e., a variable; i.e, a column of the matrix) whose reduced cost is negative (i.e., which will mean it is convenient to include it in the formulation). At this point one can notice that number of possible patterns exponentially large,and all the patterns are not even known explicitly. The question then is:
Given a basic optimal solution for the problem in which only some variables are included, how can we find (if any exists) a variable with negative reduced cost (i.e., a constraint violated by the current dual solution)?
This question can be transformed into an optimization problem: in order to see whether a variable with negative reduced cost exists, we can look for the minimum of the reduced costs of all possible variables and check whether this minimum is negative:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{c}=1-u^Tz}
Because every column of the constraint matrix corresponds to a cutting pattern, and every entry of the column says how many pieces of a certain type are in that pattern. In order for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z } to be a possible column of the constraint matrix, the following condition must be satisfied:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle \begin{matrix}z_k\in \Zeta_+\forall k\in K \\ \ \sum_kL_kz_k \leq M \end{matrix} }
And by so doing, it enables the conversion of the problem of finding a variable with negative reduced cost into the integer linear programming problem below:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix}\min\ \bar{c} = 1 - sum_{k=1}^K u_k \times z_k \\ \ s.t. \sum_kL_kz_k \leq M \\ z_k\in \Zeta_+\forall k\in K \end{matrix} }
which, in turn, would be equivalent to the below formulation (we just write the objective in maximization form and ignore the additive constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} ):
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix} \max\sum_{k=1}^K u_k \times z_k \\ \ s.t. \sum_kL_kz_k \leq M \\ z_k\in \Zeta_+\forall k\in K \end{matrix}}
The coefficients Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_k } of a column with negative reduced cost can be found by solving the above integer "knapsack" problem (which is a traditional type of problem that we find in integer programming).
In our example, if we start from the problem restricted to the five single-item patterns, the above problem reads as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \text{min} & ~~ 0.067z_{1}+0.167z_{2}+0.167z_{3}+0.167z_{4}+z_{5}\\ \text{s.t} & ~~ 6z_{1} +13.5z_{2}+15z_{3}+16.5z_{4}+22.5z_{5}\le 33\\ \ & ~~ z_{1},z_{2},z_{3},z_{4},z_{5}\ge 0\\ \end{align}}
which has the following optimal solution: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z^T= [1 \quad 0\quad 0\quad 0\quad 1]}
This matches the pattern we called Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D6} , earlier on in this page.
Optimality test
If : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle \sum_{k=1}^{K}z_{k}^{*}u_{k}^{*}\leq 1}
then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y^*} is an optimal solution of the full continuous relaxed problem (that is, including all patterns in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle S} )
If this condition is not true, we go ahead and update the master problem by including in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle S^'} the pattern Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} defined by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_{s,\lambda}} (in practical terms this means that the column Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y^*} needs to be included in the constraint matrix)
For this example we find that the optimality test is met as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{k=1}^{K}z_{k}^{*}u_{k}^{*}=0.4 \leq 1} so we have have found an optimal solution of the relaxed continuous problem (if this was not the case we would have had to go back to reformulating and solving the master problem, as discussed in the methodology section of this page)
Algorithm discussion
The column generation subproblem is the critical part of the method is generating the new columns. It is not reasonable to compute the reduced costs of all variables Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_s } for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s=1,...,S} , otherwise this procedure would reduce to the simplex method. In fact, nFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} can be very large (as in the cutting-stock problem) or, for some reason, it might not be possible or convenient to enumerate all decision variables. This is when it would be necessary to study a specific column generation algorithm for each problem; only if such an algorithm exists (and is practical), the method can be fully applied. In the one-dimensional cutting stock problem, we transformed the column generation subproblem into an easily solvable integer linear programming problem. In other cases, the computational effort required to solve the subproblem is too high, such that appying this full procedure becomes unefficient.
Applications
As previously mentioned, column generation techniques are most relevant when the problem that we are trying to solve has a high ratio of number of variables with respect to the number of constraints. As such some common applications are:
- Bandwith packing
- Bus driver scheduling
- Generally, column generation algorithms are used for large delivery networks, often in combination with other methods, helping to implement real-time solutions for on-demand logistics. We discuss a supply chain scheduling application below.
Bandwidth packing
The objective of this problem is to allocate bandwidth in a telecommunications network to maximize total revenue. The routing of a set of traffic demands between different users is to be decided, taking into account the capacity of the network arcs and the fact that the traffic between each pair of users cannot be split The problem can be formulated as an integer programming problem and the linear programming relaxation solved using column generation and the simplex algorithm. A branch and bound procedure which branches upon a particular path is used in this particular paper[12] that looks into bandwidth routing, to solve the IP. The column generation algorithm greatly reduces the complexity of this problem.
Bus driver scheduling
Bus driver scheduling aims to find the minimum number of bus drivers to cover a published timetable of a bus company. When scheduling bus drivers, contractual working rules must be enforced, thus complicating the problem. A column generation algorithm can decompose this complicated problem into a master problem and a series of pricing subproblems. The master problem would select optimal duties from a set of known feasible duties, and the pricing subproblem would augment the feasible duty set to improve the solution obtained in the master problem.[13]
Supply Chain scheduling problem
A typical application is where we consider the problem of scheduling a set of shipments between different nodes of a supply chain network. Each shipment has a fixed departure time, as well as an origin and a destination node, which, combined, determine the duration of the associated trip. The aim is to schedule as many shipments as possible, while also minimizing the number of vehicles utilized for this purpose. This problem can be formulated by an integer programming model and an associated branch and price solution algorithm. The optimal solution to the LP relaxation of the problem can be obtained through column generation, solving the linear program a huge number of variables, without explicitly considering all of them. In the context of this application, the master problem schedules the maximum possible number of shipments using only a small set of vehicle-routes, and a column generation (colgen) sub-problem would generate cost-effective vehicle-routes to be fed fed into the master problem. After finding the optimal solution to the LP relaxation of the problem, the algorithm would branch on the fractional decision variables (vehicle-routes), in order to reach the optimal integer solution.[14]
Conclusions
Column generation is a way of starting with a small, manageable part of a problem (specifically, with some of the variables), solving that part, analyzing that interim solution to find the next part of the problem (specifically, one or more variables) to add to the model, and then solving the full or extended model. In the column generation method, the algorithm steps are repeated until an optimal solution to the entire problem is achieved.[15]
This algorithm provides a way of solving a linear programming problem adding columns (corresponding to constrained variables) during the pricing phase of the problem solving phase, that would otherwise be very tedious to formulate and compute. Generating a column in the primal formulation of a linear programming problem corresponds to adding a constraint in its dual formulation.
References
- ↑ J. Desrosiers, M. L¨ubbecke, G. Desaulniers, J. B. Gauthier (June 2024). Branch-and-Price, Les Cahiers du GERAD G–2024–36, HEC Montr´eal, Canada. Revised version: October 2024
- ↑ Desrosiers, Jacques & Lübbecke, Marco. (2006). A Primer in Column Generation.p7-p14 10.1007/0-387-25486-2_1.
- ↑ 3.0 3.1 Wolsey, L. A. (2021). Integer Programming (2nd ed.). Wiley. Section 11.4, Solving the Master Problem: Branch-and-Price, pp. 219-222.
- ↑ AlainChabrier, Column Generation techniques, 2019 URL: https://medium.com/@AlainChabrier/column-generation-techniques-6a414d723a64
- ↑ AlainChabrier, Column Generation techniques, 2019 URL: https://medium.com/@AlainChabrier/column-generation-techniques-6a414d723a64
- ↑ Dantzig-Wolfe decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dantzig-Wolfe_decomposition&oldid=50750
- ↑ Wikipedia, the free encyclopeda. Column Generation. URL: https://en.wikipedia.org/wiki/Column_generation
- ↑ L.A. Wolsey, Integer programming. Wiley,Column Generation Algorithms p185-p189,1998
- ↑ GERARD. (2005). Personnel and Vehicle scheduling, Column Generation, slide 12. URL: https://slideplayer.com/slide/6574/
- ↑ L.A. Wolsey, Integer programming. Wiley,Column Generation Algorithms p185-p189,1998The Cutting Stock problem
- ↑ Gilmore, P. C., & Gomory, R. E. (1961). A Linear Programming Approach to the Cutting-Stock Problem. Operations Research, 9(6), 849-859. INFORMS.
- ↑ Parker, Mark & Ryan, Jennifer. (1993). A column generation algorithm for bandwidth packing. Telecommunication Systems. 2. 185-195. 10.1007/BF02109857.
- ↑ Dung‐Ying Lin, Ching‐Lan Hsu. Journal of Advanced Transportation. Volume50, Issue8, December 2016, Pages 1598-1615. URL: https://onlinelibrary.wiley.com/doi/abs/10.1002/atr.1417
- ↑ Kozanidis, George. (2014). Column generation for scheduling shipments within a supply chain network with the minimum number of vehicles. OPT-i 2014 - 1st International Conference on Engineering and Applied Sciences Optimization, Proceedings. 888-898
- ↑ ILOG CPLEX 11.0 User's Manual > Discrete Optimization > Using Column Generation: a Cutting Stock Example > What Is Column Generation? 1997-2007. URL:http://www-eio.upc.es/lceio/manuals/cplex-11/html/usrcplex/usingColumnGen2.html#:~:text=In%20formal%20terms%2C%20column%20generation,method%20of%20solving%20the%20problem.&text=By%201960%2C%20Dantzig%20and%20Wolfe,problems%20with%20a%20decomposable%20structure

