Sparse Reconstruction with Compressed Sensing: Difference between revisions
Molokaicat (talk | contribs) Created page with "Author: Ngoc Ly (SysEn 5800 Fall 2021)" |
Molokaicat (talk | contribs) No edit summary |
||
| (582 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
Author: Ngoc Ly (SysEn 5800 Fall 2021) | Author: Ngoc Ly (SysEn 5800 Fall 2021) | ||
<!--[[File:panic_need_more_data.png|center|thumb|600x600px]] --> | |||
<!--[[File:Page_rewrite.png|650px|Image: 650 pixels|frameless|center|rewrite]] --> | |||
== Introduction == | |||
=== Goal=== | |||
The goal of compressed sensing is to solve the underdetermined linear system in which the number of variables is much greater than the number of observations, resulting in an infinite number of signal coefficient vectors <math>x</math> for the same set of compressive measurements <math>y</math>. The objective is to reconstruct a vector <math>x</math> in a given of measurements <math>y</math> and a sensing matrix A. Instead of taking a large number of | |||
high-resolution measurements and discarding the majority of them, consider taking far fewer random measurements and reconstructing the original <math>x</math> with high probability from its sparse representation. | |||
=== Basic Idea and Notation === | |||
Begin with a linear equation <math>y = A x + e</math>, given a sensing matrix <math>A \in \mathbb{R}^{M \times N}</math> is random Gaussian or Bernouli will result in either exact or approximated optimum solution depending on how it is chosen, <math>x \in \mathbb{R}^{N}</math> is a signal vector with at most <math>k</math>-sparse entries, which means <math>x</math> has <math>k</math> non-zero entries, <math>[ N ] = \{ 1, \dots , N \} </math> be an index set, <math>y \in \mathbb{R}^{M}</math> is a compressed measurement vector, <math>[ M ] = \{ 1, \dots , M \} </math>, <math>e \in \mathbb{R}^{M}</math> is a noise vector and assumed to be bounded <math>\| e \|_2 \leq \eta</math> if it exists, and <math>M \ll N</math> read as <math>M</math> much less than <math>N</math>. | |||
=== Sparsity === | |||
A vector <math>x</math> is said to be <math>k</math>-sparse in <math>\mathbb{R}^N</math> | |||
if it has at most <math>k</math> nonzero coefficients. | |||
The support of <math>x</math> is <math>supp(x) = \{i \in [N] : x_i \neq 0 \}</math>, and <math>x</math> is a <math>k</math>-sparse signal when the cardinality <math>|supp(x)| \leq k</math>. | |||
The set of <math>k</math>-sparse vectors is denoted by <math>\Sigma_k = \{x \in \mathbb{R}^N : \|x\|_0 \leq k \}</math>. | |||
Consequently, there are <math>\binom{N}{k}</math> different subsets of <math>k</math>-sparse vectors. If a random <math>k</math>-sparse <math>x</math> is drawn uniformly from <math>\Sigma_k</math>, | |||
its entropy, <math>\log \binom{N}{k}</math>, is approximately equivalent to <math>k \log \frac{N}{k}</math> bits are required for compression of <math>\Sigma_k</math> <ref name = "Laska"/><ref name = "Coluccia"/>. | |||
The idea is to search for the sparsest <math>x \in \Sigma_k</math> from the measurement vector <math>y \in \mathbb{R}^M</math> and a sensing matrix <math>A \in \mathbb{R}^{M \times N}</math> with <math>M \ll N </math>. If the number of linear measurements is at least twice as its sparsity <math>x</math>, i.e., <math>M \geq 2k</math>, then there exists at most one signal <math>x \in \Sigma_k</math> that satisfies the constraint <math>y = A x</math> and produce the correct result for any <math>x \in \Sigma_k</math> <ref name = "Coluccia"/>. Hence, the reconstruction problem can be formulated as an <math>l_0</math>"norm" program. | |||
<math>\hat{x} = \underset{x \in \Sigma_k}{arg min} \|x\|_0 \quad s.t. \quad y = A x</math> | |||
This optimization problem minimizes the number of nonzero entries of <math>x</math> subject to the constraint <math>y = Ax </math>, that is to find the sparsest element in the affine space <math>\{ x \in \mathbb{R}^N : A x = y\}</math> <ref name = "Koep"/>. It turns out to be a combinatorial optimization problem, which is NP-Hard<ref name="Foucart"/> because it includes all possible sets of <math>k</math>-sparse out of <math>[N]</math>. Furthermore, if noise is present, the recovery is unstable [Buraniuk "compressed sensing"]. | |||
=== Restricted Isometry Property (RIP) === | |||
A matrix <math>A</math> is said to satisfy the RIP of order <math>k</math> if for all <math>x \in \Sigma_k</math> has a <math>\delta_k \in [0, 1)</math>. A restricted isometry constant (RIC) of <math>A</math> is the smallest <math>\delta_k</math> satisfying this condition <ref name = "CRT 2005"/><ref name = "Candes Tao"/><ref name = "Baraniuk 2008"/>. | |||
<math>(1 - \delta_k) \| x \|_2 ^2 \leq \| A x \|_2^2 \leq (1 + \delta_k) \| x \|_2 ^2</math> | |||
Under projections through matrix <math>A</math>, the restricted isometry property allows <math>k</math>-sparse vectors to have unique measurement vectors <math>y</math>. If <math>A</math> meets RIP, then <math>A</math> does not send two distinct <math>k</math>-sparse <math>x \in \Sigma_k</math> to the same measurement vector <math>y</math>, indicating that <math>x</math> is a unique solution under RIP. | |||
If the matrix <math>A \in \mathcal{R}^{M \times N}</math> satisfies the RIP condition of order <math>2k</math> and the constant <math>\delta_{2k} \in [0,1)</math>, there are two distinct <math>k</math>-sparse vectors in <math>\Sigma_{2k}</math>. When they are equal, the restricted isometry property holds. If <math>A</math> is a <math>2k</math>-order RIP matrix, it means that no two <math>k</math>-sparse vectors are mapped to the same measurement vector <math>y</math> by <math>A</math>. In other words, when working with sparse vectors, the RIP ensures that the columns of <math>A</math> are nearly orthonormal. Furthermore, <math>A</math> is an approximately norm-preserving function, which means that it preserves its distance when mapping for <math>k</math>-sparse signals for all or more as <math>\delta_k</math> approaches zero. Candes, Romberg, and Tao <ref name = "CRT 2005"/> proved that if <math>x</math> is <math>k</math>-sparse, and <math>A</math> satisfies the RIP of order <math>2k</math> with RIP-constant <math>\delta_{2k} < \sqrt(2) - 1</math>, then <math>\ell_1</math> gives a unique sparse solution. The <math>\ell_1</math> convex optimization problem is the same as the solution to the <math>\ell_0</math> program and can solve by the Linear Program <ref name = "Koep" /> <ref name = "Coluccia"/>. Hence, the <math>\ell_1</math> reconstruction problem is as followed which can be solved by basis pursuit <ref name = "CRT 2005"/> <ref name = "Donoho"/>. | |||
<math>\hat{x} = \underset{x \in \Sigma_k}{arg min} \|x\|_1 \quad s.t. \quad y = A x</math> | |||
<!-- | |||
== Junk == | |||
The goal of compressed sensing is to being with the under determined linear system | |||
<math>y = \Phi x + e</math>, Where <math>\Phi \in \mathbb{R}^{M \times N}</math> | |||
for | |||
<math>M \ll N</math> | |||
How can we reconstruct x from | |||
The goal is to reconstruct <math>x \in \mathbb{R}^N</math>given <math>y</math> and <math>\Phi</math> | |||
Considerably fewer random measurements and reconstruct the original <math>x</math> with high probability from its sparse representation instead of taking a large number of high-resolution measurements and discarding the majority of them. being a random matrix | |||
let <math>[ N ] = \{ 1, \dots , N \} </math>be an index set <math>[N]</math> enumerates the columns of <math>\Phi</math> and <math>x</math>. <math>\Phi</math> is an under determined systems with infinite solutions since <math>M \ll N</math>. Why <math>\ell_2</math> norm won't give sparse solutions, where asl <math>\ell_1</math> norm will return a sparse solution. | |||
==== Notation ===== | |||
<math>x \in \mathbb{R}^N</math>often not really sparse but approximately sparse | |||
<math>\mathbf{x} \in \mathbb{R}^{N}</math> | |||
<math>\Phi \in \mathbb{R}^{M \times N}</math>for <math>M \ll N</math> Sensing matrix a Random Gaussian or Bernoulli matrix | |||
<math>y \in \mathbb{R}^M</math>are the observed y samples | |||
<math>e \in \mathbb{R}^M</math>noise vector <math>\| e \|_2 \leq \eta</math> | |||
put defn of p norm here | |||
<math>x = \Psi \alpha</math> where <math>\Psi</math> is the sparsifying matrix and <math>\alpha</math> are coefficients | |||
In other words, only the smallest support set of <math>x</math> is of interest, i.e., <math>min(supp(x))</math>. | |||
The goal is to search for the sparsest <math>x \in \Sigma_k</math> given the meassurment <math>y</math> and the constraint matrix <math>\Phi</math>. | |||
This is antiquated to find the <math>\min \|x\|_0</math> in the set <math>\{ x \in \mathbb{R}^N : \Phi x = y\}</math> | |||
This searching problem can be formulated to the following <math>\ell_0</math> program | |||
Another words we are interested in the smallest <math>supp(x)</math> , i.e. <math>min(supp(x))</math> | |||
The problem formulation is to recover sparse data <math>\mathbf{x} \in \mathbb{R}^N</math>m | |||
=== sub module=== | |||
Let <math>\Phi \in \mathbb{R}^{M \times N}</math> satisfy RIP, Let <math>[N]</math> be an index set For <math>s</math> is a restriction on <math>\mathbf{x}</math> denoted by <math>x_{|s}</math> <math>x \in \mathbb{R}^N</math> to <math>s</math> k-sparse <math>\mathbf{x}</math> s.t. RIP is satisfied the <math>s = supp(\mathbf{x})</math> i.e. <math>s \subseteq [N]</math>and <math>\Phi_{|s} \subseteq \Phi</math> where the columns of <math>\Phi_{|s}</math> is indexed by <math>i \in S</math> | |||
In search for a unique solution we have the following <math>\ell_0 = |supp(x)|</math> optimization problem. | |||
=== sub module zero norm program === | |||
<math>\mathbf{\hat{x}} = \underset{\Sigma_k}{arg min} \| \mathbf{x}\|_0 \quad s.t. \quad \mathbf{y} = \Phi \mathbf{x}</math>, which is an combinatorial NP-Hard problem. Hence, if noise is presence the recovery is not stable. [Buraniuk "compressed sensing"] | |||
The goal of compressed sensing is to being with the under determined linear system | |||
<math>y = \Phi x + e</math>, Where <math>\Phi \in \mathbb{R}^{M \times N}</math> | |||
for | |||
<math>M \ll N</math> | |||
How can we reconstruct x from | |||
The goal is to reconstruct <math>x \in \mathbb{R}^N</math>given <math>y</math> and <math>\Phi</math> | |||
Considerably fewer random measurements and reconstruct the original <math>x</math> with high probability from its sparse representation instead of taking a large number of high-resolution measurements and discarding the majority of them. being a random matrix | |||
let <math>[ N ] = \{ 1, \dots , N \} </math>be an index set <math>[N]</math> enumerates the columns of <math>\Phi</math> and <math>x</math>. <math>\Phi</math> is an under determined systems with infinite solutions since <math>M \ll N</math>. Why <math>\ell_2</math> norm won't give sparse solutions, where asl <math>\ell_1</math> norm will return a sparse solution. | |||
==== Notation ===== | |||
<math>x \in \mathbb{R}^N</math>often not really sparse but approximately sparse | |||
<math>\mathbf{x} \in \mathbb{R}^{N}</math> | |||
<math>\Phi \in \mathbb{R}^{M \times N}</math>for <math>M \ll N</math> Sensing matrix a Random Gaussian or Bernoulli matrix | |||
<math>y \in \mathbb{R}^M</math>are the observed y samples | |||
<math>e \in \mathbb{R}^M</math>noise vector <math>\| e \|_2 \leq \eta</math> | |||
put defn of p norm here | |||
<math>x = \Psi \alpha</math> where <math>\Psi</math> is the sparsifying matrix and <math>\alpha</math> are coefficients | |||
If <math>A</math> satisfies RIP then <math>A</math> doesn't send two distinct | |||
k-sparse <math>x \in \Sigma_k</math> to the same measurment vector <math>y</math>. Anothers words | |||
<math>x</math> is a unique solution under RIP. | |||
RIP defined as | |||
<math>\Phi</math> satisfies RIP of order <math>k</math> if for | |||
<math>\forall x \in \Sigma_k</math> | |||
<math>\delta_k \in [0, 1)</math> satisfies for inequalaty | |||
#TODO switch s to k | |||
=== sub module RIP matracies === | |||
If a sensing matrix <math>\Phi</math>must satisfy RIP, then the number of measurements | |||
<math>M = \mathcal{O}(K/log(N/K))</math> is required recover <math>x</math> | |||
with high probability. | |||
=== sub module RIC === | |||
Restricted Isometry Constant (RIC) is the smallest <math>\delta_{|s}</math> in | |||
<math>\{\delta_k \in [0, 1): (1 - \delta_s) \| x \|_2 ^2 \leq \| \Phi x \|_2^2 \leq (1 + \delta_s) \| x \|_2 ^2\}</math> | |||
if <math>M \geq 2k</math> i.e. twise the sparsity, then there exists an unique <math>x</math> such that | |||
<math>y = \Phi x</math>. | |||
for <math>x</math> is k-sparse and | |||
and <math>\Phi</math> satisfies RIP of order <math>2k</math> | |||
RIC <math>\delta_{2k} < \sqrt{2} - 1</math> then the <math>l_0</math> | |||
program can have to relaxed convex form <math>\ell_1</math> program. | |||
If <math>\Phi</math> satisfies RIP and <math>\mathbf{y}</math> is sparse the <math>\ell_0</math> gives sparse solutions and is a unique. It is equivalent to the following <math>\ell_1</math> convex optimization problem and can solve by Linear Program. | |||
=== sub problem 1 norm program === | |||
From Results of Candes, Romberg, Tao, and Donoho | |||
<math>\mathbf{\hat{x}} = \underset{s}{arg min} \| \mathbf{x}\|_1 \quad s.t. \quad \mathbf{y} = \Phi \mathbf{x}</math> | |||
Let <math>\Phi \in R^{M \times N}</math>, the mutual coherence <math>\mu_\Phi</math> is defined by:<nowiki></math></nowiki> | |||
<math>\mu_{\Phi} = \underset{i \neq j} {\frac{| \langle a_i, a_j \rangle |}{ \| a_i \| \| a_j \|}}</math> | |||
#TODO switch s to k | |||
<math>(1 - \mu) \| x \|_2 ^2 \leq \| \Phi x \|_2^2 \leq (1 + \mu) \| x \|_2 ^2</math> | |||
Welch bound <math>\mu_\Phi \geq \sqrt{\frac{n}{m(n-m)}}</math>> <math>\mu \geq \sqrt{\frac{N -M}{M(N-1)}}</math>> is the coherence between <math>\Phi</math> and <math>\Psi</math> | |||
We want a small <math>\mu_{\Phi}</math> because it will be close to the normal matrix, which satisfies RIP. Also, <math>\mu_{\Phi}</math> will be needed for the step size for the following IHT. | |||
Need to make the connection of Coherence to RIP and RIC. | |||
#TODO switch s to k | |||
<math>(1 - \mu) \| x \|_2 ^2 \leq \| \Phi x \|_2^2 \leq (1 + \mu) \| x \|_2 ^2</math> | |||
Gel’fand n-width | |||
--> | |||
== Theory and Algorithmic Discussions == | |||
Two main things need to be considered when recovering <math>x</math> | |||
* (1) '''The design of the sensing matrix''' | |||
* (2) '''The recovery algorithm''' | |||
==== Sparsity order <math>k</math> ==== | |||
<math>k \leq C_{M}\log\left(\frac{N}{M}\right)</math> <ref name="Cohen"/><ref name="Jia"/><ref name="ShuxingLiFinite"/> | |||
TODO determining <math>k</math> for deterministic sensing matrices isn't the same as the random case <ref name="DeVore"/>. | |||
==== Mutual Coherence ==== | |||
The recovery algorithm often refers to the measurement of quantities that are appropriate to the measurement matrix (sensing matrix), i.e., the coherence. A small coherence implies the RIP condition with high probability. In general, the performance of the recovery algorithm gets better if the coherence is getting smaller. It means the columns of the matrices that have medium size are well-conditioned (governed). | |||
Let <math>A \in R^{M \times N}</math> and assume <math>\ell_2</math>-normalized columns of <math>A</math>, the mutual coherence <math>\mu = \mu(A)</math> is defined by | |||
<math>\mu(A) = \underset{1 \leq i \neq j \leq N}{max} {\frac{| \langle a_i, a_j \rangle |}{ \| a_i \|_2 \| a_j \|_2}}</math>, where <math>a_i</math> is the <math>i</math>th column of <math>A</math><ref name = "Foucart"/>. | |||
The feasibility of attaining the lower bounds for the coherence of a matrix <math>A \in R^{M \times N}</math>, <math>M < N</math> with <math>\ell_2</math>-normalized columns, and the columns of the matrix are equiangular tight frames defined as the Welch bound. | |||
<math>\mu(A) \geq \sqrt{\frac{N - M}{M(N-1)}}</math> <ref name = "Foucart"/> Sensing matrices using the Welch bound will imply a RIP of order <math>k = O (M^{1/2})</math>. <ref name="Jia"/><ref name="ShuxingLiFinite"/> | |||
However a sensing matrix <math>A</math> has two constraints a small coherence and <math>M \ll N</math> makes it impossible to satisfy the Welch bound<ref name = "Foucart"/>. <math>N</math> for an <math>\ell_2</math> must be <math>N \leq \frac{M(M+1)}{2}</math> for <math>A \in \mathbb{R}^{M \times N}</math>. This means that <math>N</math> can't be arbitrarily large and still satisfy the Welch bound. <ref name = "Foucart"/> | |||
Let a matrix <math>A \in R^{M \times N}</math> with <math>\ell_2</math>-normalized columns and let <math>s \in [N]</math>. for all <math>k</math> sparse <math>x \in \Sigma_k</math>. | |||
<math>(1 - \mu(s-1)) \| x \|_2 ^2 \leq \| A x \|_2^2 \leq (1 + \mu(s-1)) \| x \|_2 ^2</math> <ref name = "Foucart"/> | |||
=== Sensing Matrix === | |||
Although the sensing matrix <math>A</math> satisfies RIP of order <math>k</math> in some situations, confirming a given matrix <math>A</math> meets RIP's criteria is NP-hard in general. As a result, designing an efficient sensing matrix is critical. These sensing matrices are responsible for signal compression at the encoder end and accurate or approximate reconstruction at the decoder end. Sensing matrices are classified as RIP or non-RIP. Non-RIP sensing matrices adhere to a weaker condition, statistical isometry property, while still ensuring high probability recover. <ref name="Jia"/> For signal compression, different sensing matrices are utilized in compressed sensing. There are random, deterministic, structural, and optimized sensing matrices are used in compressed sensing <ref name ="Parkale" />. | |||
* '''Random Sensing Matrices''' | |||
Some classes of random matrices satisfy RIP, specifically those matrices with independent and identically distributed (i.i.d.) entries drawn from a sub-Gaussian distribution. It requires the number of measurements, <math>M = O(k log(N/k))</math> <ref name = "CRT 2005"/> <ref name = "CRT 2006"/> <ref name = "Donoho"/>, to recover <math>x</math> with high probability. Other popular random sensing matrices are Gaussian, Bernoulli, or Rademacher distributions i.e. matrix with entries <math>\{0, \pm 1\}</math>. (give examples) However, the high memory storage costs of random dense matrices render them impractical for large-scale applications. Second, despite the fact that random matracies have a high probability of satisfying RIP, there is no efficient algorithm for verifying RIP for random matracies (Li, Gao, Ge, Zhang) <ref name = "ShuxingLiCurves"/>. Several researchers have turned to sparse measurement matrices such as binary or bi-adjacency matrices rather than random matrices to address this issue. Nonetheless, those sparse matrices are unstructured in the same way that acyclic networks or trees are. Fortunately, the new random Weibull matrices ~ cite (Xiaoya Zhang and Song Li) give time of failure example. are built with appropriate observations and provide exact sparse signal reconstruction with a greater probability <ref name ="Parkale" />. | |||
===Weibull Example=== | |||
* '''Deterministic Sensing Matrices''' | |||
Although deterministic sensing matrices are insufficient to satisfy the RIP condition, they can be used to provide instances for novel concepts. Unlike a random sensing matrix such Gaussian or Bernouli there is no such <math>k = M/\log{\left(\frac{N}{M}\right)}</math> for a deterministic construction<ref name="DeVore" />. The Vandermond <math>k \times N</math> matrices are one of the best deterministic matrices for recovering the <math>k</math>-sparse signal; however, the reconstruction technique gets unstable as <math>N</math> rises. Despite the lack of RIP support in the non-RIP deterministic sensing matrices, it successfully recovered the original sparse signal for the chirp function-based employing <math>M \times M^2</math> complex-valued deterministic matrices <ref name="Applebaum"/><ref name="Jia"/>. Proved binary, bipolar, and ternary matrices are deterministic constructions of sensing matrices that satisfy the RIP of order <math>k</math> <ref name = "Amini"/> Arash Amini and Farokh Marvasti. Because of the cyclic feature, the reconstruction process can be sped up using a fast Fourier transform (FFT) technique. Another type of deterministic CS sensing matrix is one based on mutual coherence. packing design in combinatorial design theory induces the connection between sensing matrices and finite geometry (Li, Ge) <ref name="ShuxingLiFinite"/> | |||
(Deterministic Construction of Sparse Sensing Matrices via Finite Geometry Theorem II.1). | |||
<math>\mu(A) \geq \frac{t - 1}{s}</math> <ref name = "ShuxingLiFinite"/> | |||
The finite geometry-based sparse binary matrices were constructed with low coherence using a Steiner system (Shuxing Li and Gennian Ge) <ref name="ShuxingLiFinite"/> it's neat so give example. The sparseness property of matrices aids in reducing storage requirements and improving the reconstruction process <ref name ="Parkale" />. | |||
===Finite Geometry Example=== | |||
* '''Structural Sensing Matrices''' | |||
Sensing technologies require structured measurement matrices to perform a variety of tasks. Those matrices can be easily created with a small number of parameters. Furthermore, structured matrices can be used to speed the recovery performance of algorithms, making these matrices suitable for large matrices. The Toeplitz akin to a linear sparse ruler and the circulant matrix a square Toeplitz matrix akin to a circular sparse ruler. The Toeplitz structure is considered weakly stationary (second-order stationary) and a covariance matrix would be cinsidered Toeplitz more percicely circulant (Robert Gray) <ref name="RGray"/>. Applications or compressed senssing that follow a Toeplitz structure In terms of second-order statistics i.e. coveriance structures allows us to utilize statistical structures (Romero, Ariananda, Tian, Leus) <ref name="beyond sparsity"/>. | |||
In terms of accuracy, signal reconstruction speed, and coherence, these matrices perform similar to i.i.d. Gaussian satisfies RIP with high probability. The new sparse block circulant matrix (SBCM) structure greatly reduces computational complexity. Other structural sensing matrices include the Hadamard matrix, which provides near-optimal assurances of recovery while requiring less complexity and so allowing for simple hardware implementation <ref name ="Parkale" />. | |||
===Toeplitz matrix Example=== | |||
* '''Optimized Sensing Matrices''' | |||
In order to accomplish high-quality signal reconstruction, the sensing matrices must satisfy RIP. | |||
Regardless of what might be expected, the RIP is difficult to verify. Another method for validating | |||
the RIP is to compute the mutual coherence between the sensing matrix and the sparse matrix or | |||
figure the Gram matrix as <math>G = A^{T} A \in \mathbb{R}^{N \times N}</math>. The objective is to | |||
improve the sensing matrix to lower coherence using numerous strategies such as the random-detecting | |||
framework-based improvement strategy using the shrinkage technique and the irregular estimation of | |||
sensing matrix improvement employing a symmetrical strategy. Another technique is to optimize the | |||
sensing matrix using a block-sparsified dictionary approach, decreasing the total inter-block and | |||
sub-block coherence of the dictionary matrix and thereby significantly increasing the reconstruction <ref name ="Parkale" /> | |||
=== Algorithms === | |||
Several big groups of algorithms are: | |||
* '''Optimization methods''': includes <math>\ell_1</math> minimization i.e. Basis Pursuit, and quadratically constraint <math>\ell_1</math> minimization i.e. basis pursuit denoising. | |||
* '''Greedy methods''': include orthogonal matching pursuit (OMP) and compressive sampling matching pursuit (CoSaMP). | |||
* '''Thresholding-based methods''': such as iterative hard thresholding (IHT) and iterative soft thresholding (IST), approximate IHT or AM-IHT. | |||
* '''Dynamic programming'''. | |||
==== Algorithm IHT ==== | |||
The <math>\ell_1</math> convex program mentioned in introduction has an equivalent nonconstraint optimization program. <ref name = "Blumensath"/> | |||
The threashholding operators is defined as: | |||
<math> \mathcal{H}_k[x] = \underset{z \in \sum_k}{argmin} \| x - z\|_2</math> | |||
selects the best-k term approximation for some k. The <math>\ell_2</math> was proved to be RIP of order | |||
<math>3k</math>. <ref name = "Candes Tao"/> With the stopping criterion is <math>\| y - A x^{(n)}\|_2 \leq \epsilon</math> | |||
<math> \ \iff \ \mbox{RIC}</math> <math>\delta_{3k} < \frac{1}{\sqrt{32}}</math> <ref name = "Blumensath"/>. | |||
In addition the <math>\hat{f{x}} = arg \underset{x \in \Sigma_k}{min} \frac{1}{n} \| f{y} - A f{x}\|_2^2 + \lambda \| f{x}\|_1</math> in statistics the <math>\ell_1</math> regularization LASSO with <math>\lambda</math> as the regularization parameter. This is the closest convex relaxation to <math>\ell_0</math> the first program mentioned in the introduction. | |||
Reducing the above loss function<math> \frac{1}{2}\| A x - y\|_2^2 </math> with the gradient | |||
<math>z_j^{(n)} = \nabla f_j(x^{(n)}) = - A_j^T( f{y} - A f{x})</math> for each iteration before pruning that is the hard threshold operator keeping the largest values while turning the values less than the threshold to zero. | |||
Then | |||
<math>x^{n+1} = \mathcal{H}\left( f{x}^{(n)} - \tau \sum_{j \in N}^{N} z_j^{(n)}\right)</math> | |||
The IHT Algorithm reads as follow | |||
* Input <math> A, y, e \ \mbox{with} \ y = A x + e</math> and <math>k</math> | |||
* output <math>IHT(y, A, \mathcal{k}) </math>, an <math>k</math>-sparse solution to <math>x</math> | |||
* Set <math>x^{(0)} = 0; n = 0</math> | |||
* While stopping criterion false do | |||
**<math>x^{(n+1)} \leftarrow \mathcal{H}_{k} \left[ x^{(n)} + A^{*} (y - A x^{(n)}) \right]</math> | |||
**<math>n \leftarrow n + 1 </math> | |||
**end while | |||
*return: <math>IHT(y, A, k) \leftarrow x^{(n)}</math> | |||
<math>A^*</math> is an Adjoint matrix i.e. the transpose of it's cofactor. | |||
== Numerical Example == | |||
=== Deterministic Matrix Example === | |||
Question 1: Calculate the mutual coherence <math>\mu(A)</math> | |||
Question 1: Does the sensing matrix satisfy the Welch? | |||
<math>M = 5</math> <math>N = 10</math> <math>N \leq \frac{5(5+1)}{2}</math> | |||
Question 2: What is the order of <math>k</math>? | |||
=== A random matrix example === | |||
<math> x = \left[ | |||
0.1779, | |||
1.1649, | |||
-0.8262 , | |||
-1.014 , | |||
-0.7975, | |||
0.1883 , 0.2648 , | |||
-0.9036 , | |||
0.9409 , 0.4295 | |||
\right] | |||
</math> | |||
<math> | |||
A = | |||
\left[ | |||
\begin{matrix} | |||
1.24302 & 0.512088 & 0.727509 & -0.621372 & -0.167216 & 1.28429 & 1.80216 & -0.860403 & -0.190791 & 0.235666\\ | |||
-0.199659 & 0.197401 & -0.496226 & 1.1034 & -1.06153 & 0.0130745 & -0.402581 & 0.788863 & 0.591947 & -0.355693\\ | |||
0.0202145 & -0.0043102 & -1.39167 & -0.873447 & 0.253648 & 1.59332 & 0.988392 & -1.32271 & -0.951241 & -0.192874\\ | |||
0.238206 & 1.43934 & -1.08785 & -0.807931 & 0.285027 & -2.64908 & -0.140972 & -0.215606 & -0.760412 & 1.77824 \\ | |||
-0.17931 & -1.31525 & -0.0348558 & -0.550808 & 0.460217 & -1.5188 & -1.45967 & 0.508893 & -0.942668 & 1.1059\\ | |||
\end{matrix} | |||
\right] | |||
</math> | |||
<math>\hat{x} = arg \underset{x \in \Sigma_x}{min} \frac{1}{a} \| y - A x\|_2^2 + \lambda \| x\|_1</math> | |||
<math>a = 2</math> | |||
<math>\lambda = 10^{-1}</math> | |||
===Iteration 1=== | |||
calculate | |||
<math>b = x + \frac{1}{a} * A^T (A x - y)</math> | |||
<math>b = [-1.1194851676858286, -0.5425433278394107, 1.1296652382901562, 3.3691735377460557, -1.7975322402864389, 0.812781461654327, -1.5305641112291442, 2.4886377108681788, 2.7744632017898994, -2.450112036057253]</math> | |||
====Thresholding ==== | |||
<math> | |||
x^{(1)} = | |||
\begin{cases} | |||
b^{1} & if \ |b^{(1)}| > \lambda / 2a\\ | |||
0 & if \ |b^{(1)}| \leq \lambda / 2a | |||
\end{cases} | |||
</math> <ref name = "Majumdar"/> | |||
Also seen | |||
<math> | |||
x^{(1)} = | |||
\begin{cases} | |||
b^{1} & if \ |b^{(1)}| > \sqrt{\lambda}\\ | |||
0 & if \ |b^{(1)}| \leq \sqrt{\lambda} | |||
\end{cases} | |||
</math> <ref name = "Rostami"/> | |||
<math>x = [-1.1194851676858286, 0.0, 1.1296652382901562, 3.3691735377460557, -1.7975322402864389, 0.812781461654327, -1.5305641112291442, 2.4886377108681788, 2.7744632017898994, -2.450112036057253]</math> | |||
Calculate the Error | |||
<math> \|A * x - y \|_2 = 24.020025581623976 </math> | |||
Calculate the new y | |||
<math>y = A x = [-7.325091157735414, 10.392457780350403, -10.669635806747262, -13.670535847170495, -5.580526608842023]</math> | |||
Check if error is less then <math>10 ^{-5} </math> | |||
=== Iteration 2=== | |||
calculate | |||
<math>b = x + \frac{1}{a} * A^T (A x - y)</math> | |||
<math>b = [-1.1194851676858286, 0.0, 1.1296652382901562, 3.3691735377460557, -1.7975322402864389, 0.812781461654327, -1.5305641112291442, 2.4886377108681788, 2.7744632017898994, -2.450112036057253]</math> | |||
====Thresholding==== | |||
[[File:Reconstruction plot.png|thumb|right]] | |||
<math> | |||
x^{(2)} = | |||
\begin{cases} | |||
b^{2} & if \ |b^{(2)}| > \lambda / 2a\\ | |||
0 & if \ |b^{(2)}| \leq \lambda / 2a | |||
\end{cases} | |||
</math> | |||
<math>x = [-1.1194851676858286, 0.0, 1.1296652382901562, 3.3691735377460557, -1.7975322402864389, 0.812781461654327, -1.5305641112291442, 2.4886377108681788, 2.7744632017898994, -2.450112036057253]</math> | |||
Calculate the Error | |||
<math> \|A * x - y \|_2 = 0.0 </math> | |||
Calculate the new y | |||
<math>y = A x = [-7.325091157735414, 10.392457780350403, -10.669635806747262, -13.670535847170495, -5.580526608842023]</math> | |||
Check if error is less then <math>10 ^{-5} </math> | |||
Stopping condition meets. | |||
== Applications and Motivations == | |||
=== Low-Rank Matrices === | |||
The Netflix Prize was accompanied by low-rank matrix recovery or the matrix completion problem. The approach then fills in the missing values in the user's ratings for movies that the user hasn't seen. These estimates are based on ratings from other users, who have similar ratings if a matrix is created with all the users as rows and the movie titles as columns. Because some users' interests will be similar and therefore overlap, it is possible to reduce the degrees of freedom significantly. This low-rank structure is frequently assumed for the problem domain of collaborative filtering <ref name = "Bennett"/><ref name = "Koep"/>. | |||
=== Dictionary Learning === | |||
The goal in dictionary learning is to infer the original dictionary as possible. Instead of using a predefined dictionary, researchers have found that learning the dictionary by obtaining "dynamic features" from training data often yields representation. Biometric features can be taken from video clips of each subject in a dataset and used to populate the dictionary's columns. Using random projections and sparse representations for iris detection for noncontact biometrics-based authentication systems from video samples has been proposed <ref name ="Pillai"/>. | |||
=== Single-pixel cameras === | |||
Single-pixel cameras or single detector imaging are used in situations when detectors are either prohibitively expensive or difficult to miniaturize. A microarray is made up of a large number of miniature mirrors that can be individually turned on and off. The mechanism behind the random sampling, which results in low coherence between measurements, is the most important component of the single-pixel camera. This microarray reflects the light from the scene, and a lens combines all of the reflected beams into one sensor, which is the single detector of the camera used to capture the image <ref name="Baraniuk lecture notes" /> <ref name = "Burger"/>. | |||
== Conclusion == | |||
The theory was a buildup from what is an inverse problem and sparsity. It develops into the <math>\ell_0</math> norm and then concludes the <math>\ell_1</math> norm, which are sufficient conditions for basis pursuit. Candes, Romberg, Tao, and Donoho<ref name = "CRT 2005"/><ref name = "Donoho"/> were the first to overcome this problem. | |||
Although the sensing matrix fulfills RIP of order k in some cases, establishing that a given matrix satisfies RIP's conditions is generally NP-hard. In many cases, verifying the sensing matrix isn't a reasonable task, so designing the sensing matrix is crucial. In addition to the computing costs, it must fulfill RIP and be well fitted to the problem domain. It demands some imagination as well as a grasp of the problem domain. It is possible to conclude that the sparse sensing matrix is the most significant components. To conclude, David Donoho saw sparsity everywhere and encouraged, mathematicians, engineers, and scientists to view problems through sparsity. | |||
== References == | |||
<references> | |||
<ref name= "Candes Tao">Emmanuel J. Candès and Terence Tao. Decoding by linear programming. IEEE</ref> | |||
<ref name = "Majumdar">Angshul Majumdar. Compressed sensing for engineers. Devices, circuits, and systems.</ref> | |||
<ref name = "Foucart">Simon Foucart and Holger Rauhut. A mathematical introduction to compressive sens- | |||
ing. Applied and numerical harmonic analysis. Birkhäuser, New York [u.a.], 2013.</ref> | |||
<ref name = "Donoho">D. L. Donoho. Compressed sensing. 52:1289–1306, 2006.</ref> | |||
<ref name = "Coluccia">Giulio Coluccia, Chiara Ravazzi, and Enrico Magli. Compressed sensing for dis- | |||
tributed systems, 2015.</ref> | |||
<ref name = "CRT 2006">E. J. Candes, J. Romberg, and T. Tao. Robust uncertainty principles: exact signal | |||
reconstruction from highly incomplete frequency information. 52:489–509, 2006.</ref> | |||
<ref name = "Rostami">Mohammed Rostami. Compressed sensing with side information on feasible re- | |||
gion, 2013.</ref> | |||
<ref name = "Laska">Laska Jason Noah. Rice university regime change: Sampling rate vs. bit-depth in | |||
compressive sensing, 2011.</ref> | |||
<ref name = "Baraniuk lecture notes">Richard G. Baraniuk. Compressive sensing [lecture notes]. IEEE Signal Processing | |||
Magazine, 24(4):118–121, 2007.</ref> | |||
<ref name = "Baraniuk 2008">Richard Baraniuk, Mark Davenport, Ronald DeVore, and Michael Wakin. A simple | |||
proof of the restricted isometry property for random matrices. 28:253–263, 2008.</ref> | |||
<ref name = "CRT 2005">Emmanuel Candes, Justin Romberg, and Terence Tao. Stable signal recovery from | |||
incomplete and inaccurate measurements. March 2005.</ref> | |||
<ref name = "Koep">Niklas Koep, Arash Behboodi, and Rudolf Mathar. An introduction to compressed | |||
sensing, 2019.</ref> | |||
<ref name = "Burger">Martin Burger, Janic Föcke, Lukas Nickel, Peter Jung, and Sven Augustin. Recon- | |||
struction methods in thz single-pixel imaging, 2019.</ref> | |||
<ref name = "Pillai">J. K. Pillai, V. M. Patel, R. Chellappa, and N. K. Ratha. Secure and robust iris | |||
recognition using random projections and sparse representations. 33:1877–1893, | |||
2011.</ref> | |||
<ref name = "Parkale">Y. V. Parkale and S. L. Nalbalwar, “Sensing Matrices in Compressed Sensing.” pp. 113–123, 2020. doi: 10.1007/978-981-32-9515-5_11.</ref> | |||
<ref name = "Blumensath">Thomas Blumensath and Mike E. Davies. Iterative hard thresholding for com- | |||
pressed sensing. May 2008.</ref> | |||
<ref name="Bennett"> Bennett, James and Stan Lanning. “The Netflix Prize.” (2007). </ref> | |||
<ref name="ShuxingLiCurves"> S. Li, F. Gao, G. Ge and S. Zhang, "Deterministic Construction of Compressed Sensing Matrices via Algebraic Curves," in IEEE Transactions on Information Theory, vol. 58, no. 8, pp. 5035-5041, Aug. 2012, doi: 10.1109/TIT.2012.2196256. </ref> | |||
<ref name="ShuxingLiFinite"> S. Li and G. Ge, "Deterministic Construction of Sparse Sensing Matrices via Finite Geometry," in IEEE Transactions on Signal Processing, vol. 62, no. 11, pp. 2850-2859, June1, 2014, doi: 10.1109/TSP.2014.2318139. </ref> | |||
<ref name="RGray"> Robert M. Gray, Toeplitz and Circulant Matrices: A Review , now, 2006. </ref> | |||
<ref name="beyond sparsity"> D. Romero, D. D. Ariananda, Z. Tian and G. Leus, "Compressive Covariance Sensing: Structure-based compressive sensing beyond sparsity," in IEEE Signal Processing Magazine, vol. 33, no. 1, pp. 78-93, Jan. 2016, doi: 10.1109/MSP.2015.2486805. </ref> | |||
<ref name ="Amini"> A. Amini and F. Marvasti, "Deterministic Construction of Binary, Bipolar, and Ternary Compressed Sensing Matrices," in IEEE Transactions on Information Theory, vol. 57, no. 4, pp. 2360-2370, April 2011, doi: 10.1109/TIT.2011.2111670. </ref> | |||
<ref name="Applebaum"> Lorne Applebaum, Stephen D. Howard, Stephen Searle, Robert Calderbank, | |||
"Chirp sensing codes: Deterministic compressed sensing measurements for fast recovery", | |||
Applied and Computational Harmonic Analysis, | |||
Volume 26, Issue 2, | |||
2009, | |||
Pages 283-290, | |||
ISSN 1063-5203, https://doi.org/10.1016/j.acha.2008.08.002 </ref> | |||
<ref name="Jia"> | |||
X. Liu and L. Jia, "Deterministic Construction of Compressed Sensing Matrices via Vector Spaces Over Finite Fields," in IEEE Access, vol. 8, pp. 203301-203308, 2020, doi: 10.1109/ACCESS.2020.3034912. | |||
</ref> | |||
<ref name="Cohen"> | |||
Albert Cohen, Wolfgang Dahmen and Ronald DeVore, | |||
"Compressed sensing and best k-term approximation", | |||
J. Amer. Math. Soc. 22 (2009), 211-231, | |||
Published electronically: July 31, 2008, | |||
DOI: https://doi.org/10.1090/S0894-0347-08-00610-3 | |||
</ref> | |||
<ref name="DeVore"> | |||
Ronald A. DeVore, | |||
"Deterministic constructions of compressed sensing matrices", | |||
Journal of Complexity, | |||
Volume 23, Issues 4–6, | |||
2007, | |||
Pages 918-925, | |||
ISSN 0885-064X, | |||
https://doi.org/10.1016/j.jco.2007.04.002. | |||
</ref> | |||
</references> | |||
<!-- | |||
References | |||
1. Luca Baldassarre, Nirav Bhan, Volkan Cevher, Anastasios Kyrillidis, and Sid- | |||
dhartha Satpathi. Group-sparse model selection: Hardness and relaxations. IEEE | |||
Transactions on Information Theory, 62:6508–6534, 2016. | |||
Trans. Inf. Theory, 51(12):4203–4215, 2005. | |||
3. Bubacarr Bah, Jannis Kurtz, and Oliver Schaudt. Discrete optimization methods | |||
for group model selection in compressed sensing. April 2019. | |||
4. Chinmay Hegde, Piotr Indyk, and Ludwig Schmidt. Approximation algorithms | |||
for model-based compressive sensing. IEEE Transactions on Information Theory, | |||
61:5129–5147, 2015. | |||
5. Stephen A. Vavasis. Elementary proof of the spherical section property for random | |||
matrices. Univer-sity of Waterloo, Waterloo,Technical report, 2009. | |||
CRC Press, Taylor & Francis Group, Boca Raton, FL, 2019. Includes bibliographical | |||
references and index.</ref> | |||
99. J. F. Benders. Partitioning procedures for solving mixed-variables programming | |||
problems. 4:238–252, 1962. | |||
10. Jean-François Cordeau, Fabio Furini, and Ivana Ljubić. Benders decomposition | |||
for very large scale partial set covering and maximal covering location problems. | |||
275:882–896, 2019. | |||
11. Manish Bansal and Parshin Shojaee. Planar maximum coverage location problem | |||
with partial coverage, continuous spatial demand, and adjustable quality of ser- | |||
vice. December 2020. | |||
13. D.L. Donoho and Y. Tsaig. Recent advances in sparsity-driven signal recovery. | |||
volume 5, pages v/713–v/716 Vol. 5, Philadelphia, PA, USA, 2005. IEEE. | |||
14. Junzhou Huang, Tong Zhang, and Dimitris Metaxas. Learning with structured | |||
sparsity. Journal of Machine Learning Research (JMLR), 12:3371–3412, 2011. | |||
15. Binbin Lu, Huabo Sun, Paul Harris, Miaozhong Xu, and Martin Charlton. | |||
Shp2graph: Tools to convert a spatial network into an igraph graph in r. 7:293. | |||
1019. Qingbao Yu, Jiayu Chen, Yuhui Du, Jing Sui, Eswar Damaraju, Jessica A. Turner, | |||
Theo G.M. van Erp, Fabio Macciardi, Aysenil Belger, Judith M. Ford, Sarah | |||
McEwen, Daniel H. Mathalon, Bryon A. Mueller, Adrian Preda, Jatin Vaidya, | |||
Godfrey D. Pearlson, and Vince D. Calhoun. A method for building a genome- | |||
connectome bipartite graph model. Journal of Neuroscience Methods, 320:64–71, may | |||
2019. | |||
20. El kadi Hellel, Samir Hamaci, and Rezki Ziani. Modelling and reliability analysis | |||
of multi-source renewable energy systems using deterministic and stochastic petri | |||
net. The Open Automation and Control Systems Journal, 10(1):25–40, nov 2018. | |||
21. Mark F. Flanagan, Vitaly Skachek, Eimear Byrne, and Marcus Greferath. Linear- | |||
programming decoding of nonbinary linear codes. | |||
IEEE Trans. Inf. Theory, | |||
55(9):4134–4154, 2009. | |||
22. Dieyan Liang and Hong Shen. Efficient algorithms for max-weighted point sweep | |||
coverage on lines. Sensors (Basel, Switzerland), 21, February 2021. | |||
24. Thomas Blumensath. Accelerated iterative hard thresholding. 92:752–756, 2012. | |||
25. Blumensath Thomas. Eaccelerated eiterative ehard ethresholding. | |||
26. N. Burak Karahanoglu, Hakan Erdogan, and S. Ilker Birbil. A mixed integer linear | |||
programming formulation for the sparse recovery problem in compressed sensing, | |||
2013. | |||
1127. Chinmay Hegde, Piotr Indyk, and Ludwig Schmidt. A nearly-linear time frame- | |||
work for graph-structured sparsity. In International Conference on Machine Learning, | |||
pages 928–937. PMLR, 2015. | |||
28. M. Sandbichler, F. Krahmer, T. Berer, P. Burgholzer, and M. Haltmeier. A novel | |||
compressed sensing scheme for photoacoustic tomography. 75:2475–2494, 2015. | |||
29. B. S. Kashin and V. N. Temlyakov. A remark on compressed sensing. 82:748–755, | |||
2007. | |||
31. Yonina C. Eldar, Patrick Kuppinger, and Helmut Bolcskei. Block-sparse signals: | |||
Uncertainty relations and efficient recovery. 58:3042–3054, 2010. | |||
32. Wandi Liang, Zixiong Wang, Guangyu Lu, and Yang Jiang. A compressed sensing | |||
recovery algorithm based on support set selection. Electronics, 10(13):1544, 2021. | |||
34. M Amin Khajehnejad, Weiyu Xu, A Salman Avestimehr, and Babak Hassibi. | |||
Weighted l 1 minimization for sparse recovery with prior information. In 2009 IEEE | |||
international symposium on information theory, pages 483–487. IEEE, 2009. | |||
35. Junzhou Huang, Tong Zhang, and Dimitris Metaxas. Learning with structured | |||
sparsity. March 2009. | |||
36. Kezhi Li and Shuang Cong. State of the art and prospects of structured sensing | |||
matrices in compressed sensing. 9:665–677, 2015. | |||
1237. Ruitao Xie and Xiaohua Jia. Minimum transmission data gathering trees for com- | |||
pressive sensing in wireless sensor networks, 2011. | |||
38. Prateek Jain, Ambuj Tewari, and Purushottam Kar. On iterative hard thresholding | |||
methods for high-dimensional m-estimation. arXiv preprint arXiv:1410.5137, 2014. | |||
39. Yanglong Lu and Yan Wang. Physics-based compressive sensing approach to mon- | |||
itor turbulent flow. 58:3299–3307, 2020. | |||
41. Junzhou Huang and Tong Zhang. The benefit of group sparsity. 38, 2010. | |||
42. Piotr Indyk and Ilya Razenshteyn. On model-based rip-1 matrices. In International | |||
Colloquium on Automata, Languages, and Programming, pages 564–575. Springer, | |||
2013. | |||
43. Bubacarr Bah, Luca Baldassarre, and Volkan Cevher. Model-based sketching and | |||
recovery with expanders, 2014. | |||
44. A. M. Geoffrion. Generalized benders decomposition. 10:237–260, 1972. | |||
45. J. F. Benders. Partitioning procedures for solving mixed-variables programming | |||
problems. 2:3–19, 2005. | |||
46. T. L. Magnanti and R. T. Wong. Accelerating benders decomposition: Algorithmic | |||
enhancement and model selection criteria. 29:464–484, 1981. | |||
47. Richard G. Baraniuk, Volkan Cevher, Marco F. Duarte, and Chinmay Hegde. | |||
Model-based compressive sensing. arXiv e-prints, page arXiv:0808.3572, August | |||
2008. | |||
--> | |||
Latest revision as of 21:46, 22 October 2023
Author: Ngoc Ly (SysEn 5800 Fall 2021)
Introduction
Goal
The goal of compressed sensing is to solve the underdetermined linear system in which the number of variables is much greater than the number of observations, resulting in an infinite number of signal coefficient vectors $ x $ for the same set of compressive measurements $ y $. The objective is to reconstruct a vector $ x $ in a given of measurements $ y $ and a sensing matrix A. Instead of taking a large number of high-resolution measurements and discarding the majority of them, consider taking far fewer random measurements and reconstructing the original $ x $ with high probability from its sparse representation.
Basic Idea and Notation
Begin with a linear equation $ y = A x + e $, given a sensing matrix $ A \in \mathbb{R}^{M \times N} $ is random Gaussian or Bernouli will result in either exact or approximated optimum solution depending on how it is chosen, $ x \in \mathbb{R}^{N} $ is a signal vector with at most $ k $-sparse entries, which means $ x $ has $ k $ non-zero entries, $ [ N ] = \{ 1, \dots , N \} $ be an index set, $ y \in \mathbb{R}^{M} $ is a compressed measurement vector, $ [ M ] = \{ 1, \dots , M \} $, $ e \in \mathbb{R}^{M} $ is a noise vector and assumed to be bounded $ \| e \|_2 \leq \eta $ if it exists, and $ M \ll N $ read as $ M $ much less than $ N $.
Sparsity
A vector $ x $ is said to be $ k $-sparse in $ \mathbb{R}^N $ if it has at most $ k $ nonzero coefficients. The support of $ x $ is $ supp(x) = \{i \in [N] : x_i \neq 0 \} $, and $ x $ is a $ k $-sparse signal when the cardinality $ |supp(x)| \leq k $. The set of $ k $-sparse vectors is denoted by $ \Sigma_k = \{x \in \mathbb{R}^N : \|x\|_0 \leq k \} $. Consequently, there are $ \binom{N}{k} $ different subsets of $ k $-sparse vectors. If a random $ k $-sparse $ x $ is drawn uniformly from $ \Sigma_k $, its entropy, $ \log \binom{N}{k} $, is approximately equivalent to $ k \log \frac{N}{k} $ bits are required for compression of $ \Sigma_k $ [1][2].
The idea is to search for the sparsest $ x \in \Sigma_k $ from the measurement vector $ y \in \mathbb{R}^M $ and a sensing matrix $ A \in \mathbb{R}^{M \times N} $ with $ M \ll N $. If the number of linear measurements is at least twice as its sparsity $ x $, i.e., $ M \geq 2k $, then there exists at most one signal $ x \in \Sigma_k $ that satisfies the constraint $ y = A x $ and produce the correct result for any $ x \in \Sigma_k $ [2]. Hence, the reconstruction problem can be formulated as an $ l_0 $"norm" program.
$ \hat{x} = \underset{x \in \Sigma_k}{arg min} \|x\|_0 \quad s.t. \quad y = A x $
This optimization problem minimizes the number of nonzero entries of $ x $ subject to the constraint $ y = Ax $, that is to find the sparsest element in the affine space $ \{ x \in \mathbb{R}^N : A x = y\} $ [3]. It turns out to be a combinatorial optimization problem, which is NP-Hard[4] because it includes all possible sets of $ k $-sparse out of $ [N] $. Furthermore, if noise is present, the recovery is unstable [Buraniuk "compressed sensing"].
Restricted Isometry Property (RIP)
A matrix $ A $ is said to satisfy the RIP of order $ k $ if for all $ x \in \Sigma_k $ has a $ \delta_k \in [0, 1) $. A restricted isometry constant (RIC) of $ A $ is the smallest $ \delta_k $ satisfying this condition [5][6][7].
$ (1 - \delta_k) \| x \|_2 ^2 \leq \| A x \|_2^2 \leq (1 + \delta_k) \| x \|_2 ^2 $
Under projections through matrix $ A $, the restricted isometry property allows $ k $-sparse vectors to have unique measurement vectors $ y $. If $ A $ meets RIP, then $ A $ does not send two distinct $ k $-sparse $ x \in \Sigma_k $ to the same measurement vector $ y $, indicating that $ x $ is a unique solution under RIP.
If the matrix $ A \in \mathcal{R}^{M \times N} $ satisfies the RIP condition of order $ 2k $ and the constant $ \delta_{2k} \in [0,1) $, there are two distinct $ k $-sparse vectors in $ \Sigma_{2k} $. When they are equal, the restricted isometry property holds. If $ A $ is a $ 2k $-order RIP matrix, it means that no two $ k $-sparse vectors are mapped to the same measurement vector $ y $ by $ A $. In other words, when working with sparse vectors, the RIP ensures that the columns of $ A $ are nearly orthonormal. Furthermore, $ A $ is an approximately norm-preserving function, which means that it preserves its distance when mapping for $ k $-sparse signals for all or more as $ \delta_k $ approaches zero. Candes, Romberg, and Tao [5] proved that if $ x $ is $ k $-sparse, and $ A $ satisfies the RIP of order $ 2k $ with RIP-constant $ \delta_{2k} < \sqrt(2) - 1 $, then $ \ell_1 $ gives a unique sparse solution. The $ \ell_1 $ convex optimization problem is the same as the solution to the $ \ell_0 $ program and can solve by the Linear Program [3] [2]. Hence, the $ \ell_1 $ reconstruction problem is as followed which can be solved by basis pursuit [5] [8].
$ \hat{x} = \underset{x \in \Sigma_k}{arg min} \|x\|_1 \quad s.t. \quad y = A x $
Theory and Algorithmic Discussions
Two main things need to be considered when recovering $ x $
- (1) The design of the sensing matrix
- (2) The recovery algorithm
Sparsity order $ k $
$ k \leq C_{M}\log\left(\frac{N}{M}\right) $ [9][10][11] TODO determining $ k $ for deterministic sensing matrices isn't the same as the random case [12].
Mutual Coherence
The recovery algorithm often refers to the measurement of quantities that are appropriate to the measurement matrix (sensing matrix), i.e., the coherence. A small coherence implies the RIP condition with high probability. In general, the performance of the recovery algorithm gets better if the coherence is getting smaller. It means the columns of the matrices that have medium size are well-conditioned (governed).
Let $ A \in R^{M \times N} $ and assume $ \ell_2 $-normalized columns of $ A $, the mutual coherence $ \mu = \mu(A) $ is defined by
$ \mu(A) = \underset{1 \leq i \neq j \leq N}{max} {\frac{| \langle a_i, a_j \rangle |}{ \| a_i \|_2 \| a_j \|_2}} $, where $ a_i $ is the $ i $th column of $ A $[4].
The feasibility of attaining the lower bounds for the coherence of a matrix $ A \in R^{M \times N} $, $ M < N $ with $ \ell_2 $-normalized columns, and the columns of the matrix are equiangular tight frames defined as the Welch bound.
$ \mu(A) \geq \sqrt{\frac{N - M}{M(N-1)}} $ [4] Sensing matrices using the Welch bound will imply a RIP of order $ k = O (M^{1/2}) $. [10][11]
However a sensing matrix $ A $ has two constraints a small coherence and $ M \ll N $ makes it impossible to satisfy the Welch bound[4]. $ N $ for an $ \ell_2 $ must be $ N \leq \frac{M(M+1)}{2} $ for $ A \in \mathbb{R}^{M \times N} $. This means that $ N $ can't be arbitrarily large and still satisfy the Welch bound. [4]
Let a matrix $ A \in R^{M \times N} $ with $ \ell_2 $-normalized columns and let $ s \in [N] $. for all $ k $ sparse $ x \in \Sigma_k $.
$ (1 - \mu(s-1)) \| x \|_2 ^2 \leq \| A x \|_2^2 \leq (1 + \mu(s-1)) \| x \|_2 ^2 $ [4]
Sensing Matrix
Although the sensing matrix $ A $ satisfies RIP of order $ k $ in some situations, confirming a given matrix $ A $ meets RIP's criteria is NP-hard in general. As a result, designing an efficient sensing matrix is critical. These sensing matrices are responsible for signal compression at the encoder end and accurate or approximate reconstruction at the decoder end. Sensing matrices are classified as RIP or non-RIP. Non-RIP sensing matrices adhere to a weaker condition, statistical isometry property, while still ensuring high probability recover. [10] For signal compression, different sensing matrices are utilized in compressed sensing. There are random, deterministic, structural, and optimized sensing matrices are used in compressed sensing [13].
- Random Sensing Matrices
Some classes of random matrices satisfy RIP, specifically those matrices with independent and identically distributed (i.i.d.) entries drawn from a sub-Gaussian distribution. It requires the number of measurements, $ M = O(k log(N/k)) $ [5] [14] [8], to recover $ x $ with high probability. Other popular random sensing matrices are Gaussian, Bernoulli, or Rademacher distributions i.e. matrix with entries $ \{0, \pm 1\} $. (give examples) However, the high memory storage costs of random dense matrices render them impractical for large-scale applications. Second, despite the fact that random matracies have a high probability of satisfying RIP, there is no efficient algorithm for verifying RIP for random matracies (Li, Gao, Ge, Zhang) [15]. Several researchers have turned to sparse measurement matrices such as binary or bi-adjacency matrices rather than random matrices to address this issue. Nonetheless, those sparse matrices are unstructured in the same way that acyclic networks or trees are. Fortunately, the new random Weibull matrices ~ cite (Xiaoya Zhang and Song Li) give time of failure example. are built with appropriate observations and provide exact sparse signal reconstruction with a greater probability [13].
Weibull Example
- Deterministic Sensing Matrices
Although deterministic sensing matrices are insufficient to satisfy the RIP condition, they can be used to provide instances for novel concepts. Unlike a random sensing matrix such Gaussian or Bernouli there is no such $ k = M/\log{\left(\frac{N}{M}\right)} $ for a deterministic construction[12]. The Vandermond $ k \times N $ matrices are one of the best deterministic matrices for recovering the $ k $-sparse signal; however, the reconstruction technique gets unstable as $ N $ rises. Despite the lack of RIP support in the non-RIP deterministic sensing matrices, it successfully recovered the original sparse signal for the chirp function-based employing $ M \times M^2 $ complex-valued deterministic matrices [16][10]. Proved binary, bipolar, and ternary matrices are deterministic constructions of sensing matrices that satisfy the RIP of order $ k $ [17] Arash Amini and Farokh Marvasti. Because of the cyclic feature, the reconstruction process can be sped up using a fast Fourier transform (FFT) technique. Another type of deterministic CS sensing matrix is one based on mutual coherence. packing design in combinatorial design theory induces the connection between sensing matrices and finite geometry (Li, Ge) [11]
(Deterministic Construction of Sparse Sensing Matrices via Finite Geometry Theorem II.1). $ \mu(A) \geq \frac{t - 1}{s} $ [11]
The finite geometry-based sparse binary matrices were constructed with low coherence using a Steiner system (Shuxing Li and Gennian Ge) [11] it's neat so give example. The sparseness property of matrices aids in reducing storage requirements and improving the reconstruction process [13].
Finite Geometry Example
- Structural Sensing Matrices
Sensing technologies require structured measurement matrices to perform a variety of tasks. Those matrices can be easily created with a small number of parameters. Furthermore, structured matrices can be used to speed the recovery performance of algorithms, making these matrices suitable for large matrices. The Toeplitz akin to a linear sparse ruler and the circulant matrix a square Toeplitz matrix akin to a circular sparse ruler. The Toeplitz structure is considered weakly stationary (second-order stationary) and a covariance matrix would be cinsidered Toeplitz more percicely circulant (Robert Gray) [18]. Applications or compressed senssing that follow a Toeplitz structure In terms of second-order statistics i.e. coveriance structures allows us to utilize statistical structures (Romero, Ariananda, Tian, Leus) [19]. In terms of accuracy, signal reconstruction speed, and coherence, these matrices perform similar to i.i.d. Gaussian satisfies RIP with high probability. The new sparse block circulant matrix (SBCM) structure greatly reduces computational complexity. Other structural sensing matrices include the Hadamard matrix, which provides near-optimal assurances of recovery while requiring less complexity and so allowing for simple hardware implementation [13].
Toeplitz matrix Example
- Optimized Sensing Matrices
In order to accomplish high-quality signal reconstruction, the sensing matrices must satisfy RIP. Regardless of what might be expected, the RIP is difficult to verify. Another method for validating the RIP is to compute the mutual coherence between the sensing matrix and the sparse matrix or figure the Gram matrix as $ G = A^{T} A \in \mathbb{R}^{N \times N} $. The objective is to improve the sensing matrix to lower coherence using numerous strategies such as the random-detecting framework-based improvement strategy using the shrinkage technique and the irregular estimation of sensing matrix improvement employing a symmetrical strategy. Another technique is to optimize the sensing matrix using a block-sparsified dictionary approach, decreasing the total inter-block and sub-block coherence of the dictionary matrix and thereby significantly increasing the reconstruction [13]
Algorithms
Several big groups of algorithms are:
- Optimization methods: includes $ \ell_1 $ minimization i.e. Basis Pursuit, and quadratically constraint $ \ell_1 $ minimization i.e. basis pursuit denoising.
- Greedy methods: include orthogonal matching pursuit (OMP) and compressive sampling matching pursuit (CoSaMP).
- Thresholding-based methods: such as iterative hard thresholding (IHT) and iterative soft thresholding (IST), approximate IHT or AM-IHT.
- Dynamic programming.
Algorithm IHT
The $ \ell_1 $ convex program mentioned in introduction has an equivalent nonconstraint optimization program. [20]
The threashholding operators is defined as: $ \mathcal{H}_k[x] = \underset{z \in \sum_k}{argmin} \| x - z\|_2 $ selects the best-k term approximation for some k. The $ \ell_2 $ was proved to be RIP of order $ 3k $. [6] With the stopping criterion is $ \| y - A x^{(n)}\|_2 \leq \epsilon $ $ \ \iff \ \mbox{RIC} $ $ \delta_{3k} < \frac{1}{\sqrt{32}} $ [20].
In addition the $ \hat{f{x}} = arg \underset{x \in \Sigma_k}{min} \frac{1}{n} \| f{y} - A f{x}\|_2^2 + \lambda \| f{x}\|_1 $ in statistics the $ \ell_1 $ regularization LASSO with $ \lambda $ as the regularization parameter. This is the closest convex relaxation to $ \ell_0 $ the first program mentioned in the introduction.
Reducing the above loss function$ \frac{1}{2}\| A x - y\|_2^2 $ with the gradient $ z_j^{(n)} = \nabla f_j(x^{(n)}) = - A_j^T( f{y} - A f{x}) $ for each iteration before pruning that is the hard threshold operator keeping the largest values while turning the values less than the threshold to zero.
Then $ x^{n+1} = \mathcal{H}\left( f{x}^{(n)} - \tau \sum_{j \in N}^{N} z_j^{(n)}\right) $
The IHT Algorithm reads as follow
- Input $ A, y, e \ \mbox{with} \ y = A x + e $ and $ k $
- output $ IHT(y, A, \mathcal{k}) $, an $ k $-sparse solution to $ x $
- Set $ x^{(0)} = 0; n = 0 $
- While stopping criterion false do
- $ x^{(n+1)} \leftarrow \mathcal{H}_{k} \left[ x^{(n)} + A^{*} (y - A x^{(n)}) \right] $
- $ n \leftarrow n + 1 $
- end while
- return: $ IHT(y, A, k) \leftarrow x^{(n)} $
$ A^* $ is an Adjoint matrix i.e. the transpose of it's cofactor.
Numerical Example
Deterministic Matrix Example
Question 1: Calculate the mutual coherence $ \mu(A) $
Question 1: Does the sensing matrix satisfy the Welch?
$ M = 5 $ $ N = 10 $ $ N \leq \frac{5(5+1)}{2} $
Question 2: What is the order of $ k $?
A random matrix example
$ x = \left[ 0.1779, 1.1649, -0.8262 , -1.014 , -0.7975, 0.1883 , 0.2648 , -0.9036 , 0.9409 , 0.4295 \right] $
$ A = \left[ \begin{matrix} 1.24302 & 0.512088 & 0.727509 & -0.621372 & -0.167216 & 1.28429 & 1.80216 & -0.860403 & -0.190791 & 0.235666\\ -0.199659 & 0.197401 & -0.496226 & 1.1034 & -1.06153 & 0.0130745 & -0.402581 & 0.788863 & 0.591947 & -0.355693\\ 0.0202145 & -0.0043102 & -1.39167 & -0.873447 & 0.253648 & 1.59332 & 0.988392 & -1.32271 & -0.951241 & -0.192874\\ 0.238206 & 1.43934 & -1.08785 & -0.807931 & 0.285027 & -2.64908 & -0.140972 & -0.215606 & -0.760412 & 1.77824 \\ -0.17931 & -1.31525 & -0.0348558 & -0.550808 & 0.460217 & -1.5188 & -1.45967 & 0.508893 & -0.942668 & 1.1059\\ \end{matrix} \right] $
$ \hat{x} = arg \underset{x \in \Sigma_x}{min} \frac{1}{a} \| y - A x\|_2^2 + \lambda \| x\|_1 $
$ a = 2 $ $ \lambda = 10^{-1} $
Iteration 1
calculate $ b = x + \frac{1}{a} * A^T (A x - y) $
$ b = [-1.1194851676858286, -0.5425433278394107, 1.1296652382901562, 3.3691735377460557, -1.7975322402864389, 0.812781461654327, -1.5305641112291442, 2.4886377108681788, 2.7744632017898994, -2.450112036057253] $
Thresholding
$ x^{(1)} = \begin{cases} b^{1} & if \ |b^{(1)}| > \lambda / 2a\\ 0 & if \ |b^{(1)}| \leq \lambda / 2a \end{cases} $ [21]
Also seen
$ x^{(1)} = \begin{cases} b^{1} & if \ |b^{(1)}| > \sqrt{\lambda}\\ 0 & if \ |b^{(1)}| \leq \sqrt{\lambda} \end{cases} $ [22]
$ x = [-1.1194851676858286, 0.0, 1.1296652382901562, 3.3691735377460557, -1.7975322402864389, 0.812781461654327, -1.5305641112291442, 2.4886377108681788, 2.7744632017898994, -2.450112036057253] $
Calculate the Error $ \|A * x - y \|_2 = 24.020025581623976 $
Calculate the new y
$ y = A x = [-7.325091157735414, 10.392457780350403, -10.669635806747262, -13.670535847170495, -5.580526608842023] $
Check if error is less then $ 10 ^{-5} $
Iteration 2
calculate $ b = x + \frac{1}{a} * A^T (A x - y) $
$ b = [-1.1194851676858286, 0.0, 1.1296652382901562, 3.3691735377460557, -1.7975322402864389, 0.812781461654327, -1.5305641112291442, 2.4886377108681788, 2.7744632017898994, -2.450112036057253] $
Thresholding
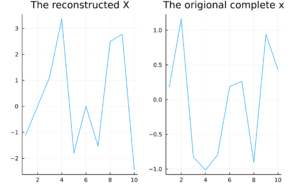
$ x^{(2)} = \begin{cases} b^{2} & if \ |b^{(2)}| > \lambda / 2a\\ 0 & if \ |b^{(2)}| \leq \lambda / 2a \end{cases} $
$ x = [-1.1194851676858286, 0.0, 1.1296652382901562, 3.3691735377460557, -1.7975322402864389, 0.812781461654327, -1.5305641112291442, 2.4886377108681788, 2.7744632017898994, -2.450112036057253] $
Calculate the Error $ \|A * x - y \|_2 = 0.0 $
Calculate the new y
$ y = A x = [-7.325091157735414, 10.392457780350403, -10.669635806747262, -13.670535847170495, -5.580526608842023] $
Check if error is less then $ 10 ^{-5} $
Stopping condition meets.
Applications and Motivations
Low-Rank Matrices
The Netflix Prize was accompanied by low-rank matrix recovery or the matrix completion problem. The approach then fills in the missing values in the user's ratings for movies that the user hasn't seen. These estimates are based on ratings from other users, who have similar ratings if a matrix is created with all the users as rows and the movie titles as columns. Because some users' interests will be similar and therefore overlap, it is possible to reduce the degrees of freedom significantly. This low-rank structure is frequently assumed for the problem domain of collaborative filtering [23][3].
Dictionary Learning
The goal in dictionary learning is to infer the original dictionary as possible. Instead of using a predefined dictionary, researchers have found that learning the dictionary by obtaining "dynamic features" from training data often yields representation. Biometric features can be taken from video clips of each subject in a dataset and used to populate the dictionary's columns. Using random projections and sparse representations for iris detection for noncontact biometrics-based authentication systems from video samples has been proposed [24].
Single-pixel cameras
Single-pixel cameras or single detector imaging are used in situations when detectors are either prohibitively expensive or difficult to miniaturize. A microarray is made up of a large number of miniature mirrors that can be individually turned on and off. The mechanism behind the random sampling, which results in low coherence between measurements, is the most important component of the single-pixel camera. This microarray reflects the light from the scene, and a lens combines all of the reflected beams into one sensor, which is the single detector of the camera used to capture the image [25] [26].
Conclusion
The theory was a buildup from what is an inverse problem and sparsity. It develops into the $ \ell_0 $ norm and then concludes the $ \ell_1 $ norm, which are sufficient conditions for basis pursuit. Candes, Romberg, Tao, and Donoho[5][8] were the first to overcome this problem.
Although the sensing matrix fulfills RIP of order k in some cases, establishing that a given matrix satisfies RIP's conditions is generally NP-hard. In many cases, verifying the sensing matrix isn't a reasonable task, so designing the sensing matrix is crucial. In addition to the computing costs, it must fulfill RIP and be well fitted to the problem domain. It demands some imagination as well as a grasp of the problem domain. It is possible to conclude that the sparse sensing matrix is the most significant components. To conclude, David Donoho saw sparsity everywhere and encouraged, mathematicians, engineers, and scientists to view problems through sparsity.
References
- ↑ Laska Jason Noah. Rice university regime change: Sampling rate vs. bit-depth in compressive sensing, 2011.
- ↑ 2.0 2.1 2.2 Giulio Coluccia, Chiara Ravazzi, and Enrico Magli. Compressed sensing for dis- tributed systems, 2015.
- ↑ 3.0 3.1 3.2 Niklas Koep, Arash Behboodi, and Rudolf Mathar. An introduction to compressed sensing, 2019.
- ↑ 4.0 4.1 4.2 4.3 4.4 4.5 Simon Foucart and Holger Rauhut. A mathematical introduction to compressive sens- ing. Applied and numerical harmonic analysis. Birkhäuser, New York [u.a.], 2013.
- ↑ 5.0 5.1 5.2 5.3 5.4 Emmanuel Candes, Justin Romberg, and Terence Tao. Stable signal recovery from incomplete and inaccurate measurements. March 2005.
- ↑ 6.0 6.1 Emmanuel J. Candès and Terence Tao. Decoding by linear programming. IEEE
- ↑ Richard Baraniuk, Mark Davenport, Ronald DeVore, and Michael Wakin. A simple proof of the restricted isometry property for random matrices. 28:253–263, 2008.
- ↑ 8.0 8.1 8.2 D. L. Donoho. Compressed sensing. 52:1289–1306, 2006.
- ↑ Albert Cohen, Wolfgang Dahmen and Ronald DeVore, "Compressed sensing and best k-term approximation", J. Amer. Math. Soc. 22 (2009), 211-231, Published electronically: July 31, 2008, DOI: https://doi.org/10.1090/S0894-0347-08-00610-3
- ↑ 10.0 10.1 10.2 10.3 X. Liu and L. Jia, "Deterministic Construction of Compressed Sensing Matrices via Vector Spaces Over Finite Fields," in IEEE Access, vol. 8, pp. 203301-203308, 2020, doi: 10.1109/ACCESS.2020.3034912.
- ↑ 11.0 11.1 11.2 11.3 11.4 S. Li and G. Ge, "Deterministic Construction of Sparse Sensing Matrices via Finite Geometry," in IEEE Transactions on Signal Processing, vol. 62, no. 11, pp. 2850-2859, June1, 2014, doi: 10.1109/TSP.2014.2318139.
- ↑ 12.0 12.1 Ronald A. DeVore, "Deterministic constructions of compressed sensing matrices", Journal of Complexity, Volume 23, Issues 4–6, 2007, Pages 918-925, ISSN 0885-064X, https://doi.org/10.1016/j.jco.2007.04.002.
- ↑ 13.0 13.1 13.2 13.3 13.4 Y. V. Parkale and S. L. Nalbalwar, “Sensing Matrices in Compressed Sensing.” pp. 113–123, 2020. doi: 10.1007/978-981-32-9515-5_11.
- ↑ E. J. Candes, J. Romberg, and T. Tao. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. 52:489–509, 2006.
- ↑ S. Li, F. Gao, G. Ge and S. Zhang, "Deterministic Construction of Compressed Sensing Matrices via Algebraic Curves," in IEEE Transactions on Information Theory, vol. 58, no. 8, pp. 5035-5041, Aug. 2012, doi: 10.1109/TIT.2012.2196256.
- ↑ Lorne Applebaum, Stephen D. Howard, Stephen Searle, Robert Calderbank, "Chirp sensing codes: Deterministic compressed sensing measurements for fast recovery", Applied and Computational Harmonic Analysis, Volume 26, Issue 2, 2009, Pages 283-290, ISSN 1063-5203, https://doi.org/10.1016/j.acha.2008.08.002
- ↑ A. Amini and F. Marvasti, "Deterministic Construction of Binary, Bipolar, and Ternary Compressed Sensing Matrices," in IEEE Transactions on Information Theory, vol. 57, no. 4, pp. 2360-2370, April 2011, doi: 10.1109/TIT.2011.2111670.
- ↑ Robert M. Gray, Toeplitz and Circulant Matrices: A Review , now, 2006.
- ↑ D. Romero, D. D. Ariananda, Z. Tian and G. Leus, "Compressive Covariance Sensing: Structure-based compressive sensing beyond sparsity," in IEEE Signal Processing Magazine, vol. 33, no. 1, pp. 78-93, Jan. 2016, doi: 10.1109/MSP.2015.2486805.
- ↑ 20.0 20.1 Thomas Blumensath and Mike E. Davies. Iterative hard thresholding for com- pressed sensing. May 2008.
- ↑ Angshul Majumdar. Compressed sensing for engineers. Devices, circuits, and systems.
- ↑ Mohammed Rostami. Compressed sensing with side information on feasible re- gion, 2013.
- ↑ Bennett, James and Stan Lanning. “The Netflix Prize.” (2007).
- ↑ J. K. Pillai, V. M. Patel, R. Chellappa, and N. K. Ratha. Secure and robust iris recognition using random projections and sparse representations. 33:1877–1893, 2011.
- ↑ Richard G. Baraniuk. Compressive sensing [lecture notes]. IEEE Signal Processing Magazine, 24(4):118–121, 2007.
- ↑ Martin Burger, Janic Föcke, Lukas Nickel, Peter Jung, and Sven Augustin. Recon- struction methods in thz single-pixel imaging, 2019.