Nadam: Difference between revisions
(Created page with "Fall 2024 new page creation") |
|||
| (47 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
Fall 2024 | Author: Vinamr Jain (vj89) (ChemE 6800 Fall 2024) | ||
Stewards: Nathan Preuss, Wei-Han Chen, Tianqi Xiao, Guoqing Hu | |||
== Introduction == | |||
Nesterov-accelerated Adaptive Moment Estimation (Nadam) is an optimization algorithm introduced by Timothy Dozat in his 2016 paper, “Incorporating Nesterov Momentum into Adam” <ref name="Dozat"> T. Dozat, “Incorporating Nesterov Momentum into Adam”.</ref>. Nadam enhances the Adaptive Moment Estimation (Adam) optimizer by integrating Nesterov momentum, aiming to improve convergence speed and performance in training deep learning models. This algorithm has been applied across various domains, including computer vision and natural language processing, to optimize neural network training. Gradient descent optimization algorithms are fundamental tools in machine learning, often employed as black-box optimizers to minimize loss functions by iteratively adjusting model parameters. Gradient Descent updates parameters by following the negative gradient of the loss function to seek a minimum, but can be slow to converge, especially in regions with flat or elongated curvatures <ref name="brownlee"> J. Brownlee, “Gradient Descent Optimization With Nadam From Scratch,” MachineLearningMastery.com. Accessed: Oct. 27, 2024. [Online]. Available: https://www.machinelearningmastery.com/gradient-descent-optimization-with-nadam-from-scratch/ </ref>. Several variants address these challenges. Momentum accelerates convergence by accumulating a decaying sum of past gradients, helping navigate ravines and reducing oscillations <ref name="Dozat" />. Nesterov’s Accelerated Gradient (NAG), also known as Nesterov momentum, improves upon Momentum by calculating the gradient at a projected future position, often resulting in faster convergence. RMSprop adapts learning rates for each parameter individually and normalizes gradients by a decaying average of recent magnitudes, effectively handling non-stationary objectives <ref name="ruder"> S. Ruder, “An overview of gradient descent optimization algorithms,” Jun. 15, 2017, arXiv: arXiv:1609.04747. doi: 10.48550/arXiv.1609.04747. </ref>. Adaptive Moment Estimation (Adam) <ref> D. P. Kingma and J. Ba, “Adam: A Method for Stochastic Optimization,” Jan. 30, 2017, arXiv: arXiv:1412.6980. doi: 10.48550/arXiv.1412.6980.</ref> combines the benefits of Momentum and adaptive learning rates, computing individual adaptive rates based on first and second moments of gradients. However, Adam may sometimes converge to suboptimal solutions due to its adaptive learning rate mechanism <ref name="ruder"/> and can slow down before reaching global optima <ref name="brownlee" />. Nadam extends Adam by incorporating Nesterov momentum, evaluating the gradient at a projected future parameter position and improving convergence speed and accuracy. | |||
== Background == | |||
Gradient Descent is a first-order iterative optimization algorithm used to find a local minimum of a differentiable function. The parameter update rule at iteration <math> t </math> is: | |||
<math> \theta_{t+1}=\theta_t-\eta\nabla_\theta J\left(\theta_t\right) </math> | |||
Where <math> \theta_t </math> denotes the parameters vector at iteration <math> t </math>, <math> \eta </math> is the learning rate, and <math> \nabla_\theta J\left(\theta_t\right) </math> is the gradient of the cost function <math> J </math> with respect to <math> \theta </math> at iteration <math> t </math>. Momentum accelerates Gradient Descent by accumulating an exponentially decaying moving average of past gradients. This accelerates gradient descent along stable gradient directions and slows it in oscillating directions <ref name="Dozat" />. | |||
<math> m_t=\gamma m_{t-1}+\eta\nabla_\theta J\left(\theta_t\right) </math> | |||
<math> \theta_{t+1}=\theta_t-m_t </math> | |||
Here in addition to the gradient component, there’s an additional term <math> m_t </math>, the momentum vector, and <math> \gamma </math> is the momentum coefficient. Nesterov Momentum improves upon standard Momentum by calculating the gradient at the anticipated future position, leading to a more responsive update. | |||
<math> m_t=\gamma m_{t-1}+\eta\nabla_\theta J\left(\theta_t-\gamma m_{t-1}\right) </math> | |||
<math> \theta_{t+1}=\theta_t-m_t </math> | |||
Alternatively, one can apply the current look-ahead momentum vector directly to update the current parameters: | |||
<math> m_t=\gamma m_{t-1}+\eta\nabla_\theta J\left(\theta_t\right) </math> | |||
<math> \theta_{t+1}=\theta_t-{(\gamma m}t\ +\ \eta{\ \nabla}\theta J\left(\theta_t\right)\ ) </math> | |||
AdaGrad (Adaptive Gradient Algorithm) adapts the learning rate for each parameter individually by scaling it inversely proportional to the square root of the sum of all historical squared values of the gradients. This method is particularly useful for dealing with sparse data <ref name="ruder" />. | |||
<math> v_t=v_{t-1}+\left[\nabla_\theta J\left(\theta_t\right)\right]^2 </math> | |||
<math> \theta_{t+1}=\theta_t-\eta\frac{\nabla_\theta J\left(\theta_t\right)}{\sqrt{v_t}+\epsilon} </math> | |||
<math> v_t </math> is the accumulated sum of squared gradients up to time <math> t </math>, and <math> \epsilon </math> is a small constant for numerical stability (e.g., <math> 10^{-8} </math>). AdaGrad effectively scales down the learning rate for parameters associated with frequently occurring features, allowing for larger updates for infrequent features <ref name="Dozat" />. | |||
RMSprop (Root Mean Square Propagation) is an optimization algorithm that builds upon AdaGrad by modifying the way it accumulates squared gradients. While AdaGrad accumulates all past squared gradients, leading to a continually decreasing learning rate, RMSprop introduces a decay parameter to the accumulated squared gradients <math> v_t </math>. This parameterization prevents the learning rate from diminishing too quickly. | |||
<math> v_t=\gamma v_{t-1}+\left(1-\gamma\right)\left[\nabla_\theta J\left(\theta_t\right)\right]^2 </math> | |||
<math> \theta_{t+1}=\theta_t-\eta\frac{\nabla_\theta J\left(\theta_t\right)}{\sqrt{v_t}+\epsilon} </math> | |||
<math> \gamma </math> is the decay rate (typically <math> \gamma=0.9 </math>). By introducing the decay parameter in the <math> v_t </math> term, RMSprop limits the influence of older gradients, ensuring that the algorithm adapts quickly to the most recent gradients. | |||
Adam (Adaptive Moment Estimation) is an optimization algorithm that combines ideas from both Momentum and RMSprop. It extends RMSprop by not only adapting the learning rates per parameter but also incorporating momentum by using an exponentially decaying average of past gradients (first moment). Adam is designed to work well with sparse gradients and noisy problems, which are common in training deep neural networks. | |||
<math> m_t=\beta_1m_{t-1}+\left(1-\beta_1\right)\nabla_\theta J\left(\theta_t\right) </math> | |||
<math> v_t=\beta_2v_{t-1}+\left(1-\beta_2\right)\left[\nabla_\theta J\left(\theta_t\right)\right]^2 </math> | |||
<math> m_t </math> is the first moment estimate (exponentially decaying average of past gradients), <math> v_t </math> is the second moment estimate (exponentially decaying average of past squared gradients), and <math> \beta_1 </math> and <math> \beta_2 </math> are the exponential decay rates for the moment estimates (commonly <math> \beta_1=0.9, \beta_2=0.999 </math>). | |||
As <math> m_t </math> and <math> v_t </math> are initialized at zero vectors, they are biased towards zero, especially during the initial time steps and particularly when the decay rates are close to one (i.e., <math> \beta_1, \beta_2\approx1 </math>). This bias can slow down the convergence of the algorithm because the moment estimates underestimate the true mean and variance of the gradients. To counteract these biases, the authors of Adam introduced bias-corrected moment estimates: | |||
<math> \widehat{m_t}=\frac{m_t}{1-\beta_1^t} </math> | |||
<math> \widehat{v_t}=\frac{v_t}{1-\beta_2^t} </math> | |||
The denominators <math> 1-\beta_1^t </math> and <math> 1-\beta_2^t </math> approach 1 as <math> t </math> increases, reducing the impact of the bias over time. The bias correction compensates for the initialization at zero, ensuring that the moment estimates are unbiased. The parameters are then updated using the bias-corrected moment estimates: | |||
<math> \theta_{t+1}=\theta_t-\eta\frac{\widehat{m_t}}{\sqrt{\widehat{v_t}}+\epsilon} </math> | |||
== Algorithm == | |||
Nadam modifies the parameter update step of Adam by integrating the Nesterov accelerated gradient. In Adam, the update relies solely on the bias-corrected first moment estimate <math> \widehat{m_t} </math>. Nadam modifies the parameter update step of Adam by integrating the Nesterov accelerated gradient. In Adam, the update relies solely on the bias-corrected first moment estimate <math> \widehat{m_t} </math>. Nadam, however, adjusts this estimate by adding a term that accounts for the current gradient, effectively looking ahead to where the parameters are heading. This adjustment is similar to the Nesterov momentum in NAG, which computes the gradient at the approximate future position of the parameters. Firstly, consider the bias-corrected first moment <math> \widehat{m_t} </math> using the definition of <math> m_t </math> <ref name="ruder" /> | |||
<math> \widehat{m_t}=\frac{m_t}{1-\beta_1^t}=\frac{\beta_1m_{t-1}+\left(1-\beta_1\right)g_t}{1-\beta_1^t} </math> | |||
Where <math> g_t=\nabla_\theta J\left(\theta_t\right) </math>. The update rule of Adam can be rewritten as | |||
<math> \theta_{t+1}=\theta_t-\frac{\eta}{\left(\sqrt{\widehat{v_t}}+\epsilon\right)}\left[\frac{\beta_1m_{t-1}}{\left(1-\beta_1^t\right)}+\frac{\left(1-\beta_1\right)g_t}{\left(1-\beta_1^t\right)}\right] </math> | |||
Recognizing that <math> \frac{\beta_1m_{t-1}}{1-\beta_1^t} </math> is the bias-corrected estimate of the momentum vector from the previous time step, let’s denote: | |||
<math> \widehat{m_{t-1}}=\frac{m_{t-1}}{1-\beta_1^{t-1}} </math> | |||
However, since <math> \beta_1^{t-1} </math> is close to <math> \beta_1^t </math> for large <math> t </math>, it can be approximated as: | |||
<math> \frac{\beta_1m_{t-1}}{1-\beta_1^t}\approx\beta_1\widehat{m_{t-1}} </math> | |||
Thus, the update rule becomes: | |||
<math> \theta_{t+1}=\theta_t-\eta\frac{\beta_1\widehat{m_{t-1}}+\frac{\left(1-\beta_1\right)g_t}{1-\beta_1^t}}{\sqrt{\widehat{v_t}}+\epsilon} </math> | |||
This form resembles the momentum term in Nesterov Accelerated Gradient (NAG). To incorporate Nesterov momentum into Adam, the previous bias-corrected momentum estimate <math> \widehat{m_{t-1}} </math> is replaced with the current estimate <math> \widehat{m_t} </math>. This aligns with the NAG approach of using the look-ahead momentum vector for updating parameters. | |||
The Nadam update rule becomes: | |||
<math> \theta_{t+1}=\theta_t-\eta\frac{\beta_1\widehat{m_t}+\frac{\left(1-\beta_1\right)g_t}{1-\beta_1^t}}{\sqrt{\widehat{v_t}}+\epsilon} </math> | |||
By combining the bias-corrected first moment estimate <math> \widehat{m_t} </math> and the current gradient <math> g_t </math>, weighted appropriately, Nadam aims to improve the responsiveness of the optimizer to recent gradient information, potentially enhancing convergence speed. | |||
=== Pseudocode === | |||
The pseudocode for Nadam is as follows: | |||
'''Algorithm Nadam Optimization Input:''' | |||
Initial parameters <math> \theta_0 </math>, learning rate <math> \eta </math>, decay rates <math> \beta_1 </math>, <math> \beta_2 </math>, small constant <math> \epsilon </math> | |||
'''Initialize''' <math> m_0\gets0,v_0\gets0,t\gets0 </math> | |||
While ''not converged'' do | |||
<math> t\ \gets t\ +\ 1 </math> | |||
'''Compute gradient:''' <math> g_t=\nabla_\theta J\left(\theta_{t-1}\right) </math> | |||
'''Update biased first moment:''' <math> m_t\gets\beta_1\cdot m_{t-1}+\left(1-\beta_1\right)\cdot g_t </math> | |||
'''Update biased second moment:''' <math> v_t\gets\beta_2\cdot v_{t-1}+\left(1-\beta_2\right)\cdot g_t^2 </math> | |||
'''Bias correction:''' <math> \widehat{m_t}\gets\frac{m_t}{1-\beta_1^t}, \widehat{v_t}\gets\frac{v_t}{1-\beta_2^t} | |||
</math> | |||
'''Nesterov adjustment:''' <math> m'_t \gets \beta_1 \cdot \widehat{m_t} + \frac{\left(1 - \beta_1\right) \cdot g_t}{1 | |||
- \beta_1^t} </math> | |||
'''Update parameters:''' <math> \theta_t \gets \theta_{t-1} - \eta \cdot \frac{m'_t}{\sqrt{\widehat{v_t}} + \epsilon} | |||
</math> | |||
'''Output:''' Optimized parameters <math> \theta_t </math> | |||
== Numerical Examples == | |||
This section provides numerical examples to illustrate how the Nadam algorithm operates. We choose a simple quadratic function to make the calculations straightforward and easy to follow, and then we demonstrate the numerical calculations for a linear regression task. | |||
=== Minimizing a Quadratic Function === | |||
Consider the cost function: | |||
<math> J\left(\theta\right)=\frac{1}{2}\theta^2 </math>which has its global minimum at <math> \theta=0 </math>. The aim is to minimize this function using the Nadam optimizer, starting from an initial parameter value of <math> \theta_0=5 </math>. | |||
The hyperparameters are set as follows: learning rate <math> \eta=0.1 </math>, exponential decay rates <math> \beta_1,\beta_2=0.9 </math>, numerical stability constant <math> \epsilon={10}^{-8} </math>, and initialize the first and second moment estimates and the time step as <math> m_0=0, v_0=0, t=0 </math>. | |||
'''Iteration 1''' | |||
1. Time Step Update: | |||
<math> t\ \gets t\ +\ 1\ =\ 1 </math> | |||
2. Compute Gradient at Current Parameter: | |||
<math> g_1=\nabla_\theta J\left(\theta_0\right)=\theta_0=5 </math> | |||
3. Update Biased First Moment Estimate: | |||
<math> m_1=\beta_1m_0+\left(1-\beta_1\right)g_1=0.9\times0+0.1\times5=0.5 </math> | |||
4. Update Biased Second Moment Estimate: | |||
<math> v_1=\beta_2v_0+\left(1-\beta_2\right)g_1^2=0.999\times0+0.001\times25=0.025 </math> | |||
5. Compute Bias-Corrected Estimates: | |||
<math> \widehat{m_1}=\frac{m_1}{1-\beta_1^t}=\frac{0.5}{1-{0.9}^1}=\frac{0.5}{0.1}=5 </math> | |||
<math> \widehat{v_1}=\frac{v_1}{1-\beta_2^t}=\frac{0.025}{1-{0.999}^1}=\frac{0.025}{0.001}=25 </math> | |||
6. Nesterov Adjustment for First Moment: | |||
<math> m\prime_1=\beta_1\widehat{m_1}+\frac{\left(1-\beta_1\right)g_1}{1-\beta_1^t}=0.9\times5+\frac{0.1\times5}{0.1}=4.5+5=9.5 </math> | |||
7. Parameter Update: | |||
<math> \theta_1=\theta_0-\eta\frac{m\prime_1}{\sqrt{\widehat{v_1}}+\epsilon}=5-0.1\times\frac{9.5}{\sqrt{25}+{10}^{-8}}=5-0.1\times\frac{9.5}{5}=5-0.1\times1.9=5-0.19=4.81 </math> | |||
'''Iteration 2''' | |||
1. Time Step Update: | |||
<math> t\ \gets t\ +\ 1\ =\ 2 </math> | |||
2. Compute Gradient at Current Parameter: | |||
<math> g_2=\nabla_\theta J\left(\theta_1\right)=\theta_1=4.81 </math> | |||
3. Update Biased First Moment Estimate: | |||
<math> m_2=\beta_1m_1+\left(1-\beta_1\right)g_2=0.9\times0.5+0.1\times4.81=0.45+0.481=0.931 </math> | |||
4. Update Biased Second Moment Estimate: | |||
<math> v_2=\beta_2v_1+\left(1-\beta_2\right)g_2^2=0.999\times0.025+0.001\times\left(4.81\right)^2=0.024975+0.001\times23.1361=0.024975+0.0231361=0.0481111 </math> | |||
5. Compute Bias-Corrected Estimates: | |||
<math> \widehat{m_2}=\frac{m_2}{1-\beta_1^t}=\frac{0.931}{1-{0.9}^2}=\frac{0.931}{1-0.81}=\frac{0.931}{0.19}\approx4.9005 </math> | |||
<math> \widehat{v_2}=\frac{v_2}{1-\beta_2^t}=\frac{0.0481111}{1-{0.999}^2}=\frac{0.0481111}{1-0.998001}=\frac{0.0481111}{0.001999}\approx24.0696 </math> | |||
6. Nesterov Adjustment for First Moment: | |||
<math> m\prime_2=\beta_1\widehat{m_2}+\frac{\left(1-\beta_1\right)g_2}{1-\beta_1^t}=0.9\times4.9005+\frac{0.1\times4.81}{0.19}=4.41045+\frac{0.481}{0.19}\approx4.41045+2.5316=6.9421 </math> | |||
7. Parameter Update: | |||
<math> \theta_2=\theta_1-\eta\frac{m\prime_2}{\sqrt{\widehat{v_2}}+\epsilon}=4.81-0.1\times\frac{6.9421}{\sqrt{24.0696}+{10}^{-8}}=4.81-0.1\times\frac{6.9421}{4.9061}=4.81-0.1\times1.4142=4.81-0.14142=4.6686 </math> | |||
'''Iteration 3''' | |||
1. Time Step Update: | |||
<math> t\ \gets t\ +\ 1\ =\ 3 </math> | |||
2. Compute Gradient at Current Parameter: | |||
<math> g_3=\nabla_\theta J\left(\theta_2\right)=\theta_2=4.6686 </math> | |||
3. Update Biased First Moment Estimate: | |||
<math> m_3=\beta_1m_2+\left(1-\beta_1\right)g_3=0.9\times0.931+0.1\times4.6686=0.8379+0.46686=1.30476 </math> | |||
4. Update Biased Second Moment Estimate: | |||
<math> v_3=\beta_2v_2+\left(1-\beta_2\right)g_3^2=0.999\times0.0481111+0.001\times\left(4.6686\right)^2=0.048063+0.001\times21.7899=0.048063+0.0217899=0.0698529 </math> | |||
5. Compute Bias-Corrected Estimates: | |||
<math> \widehat{m_3}=\frac{m_3}{1-\beta_1^t}=\frac{1.30476}{1-{0.9}^3}=\frac{1.30476}{1-0.729}=\frac{1.30476}{0.271}\approx4.8134 </math> | |||
<math> \widehat{v_3}=\frac{v_3}{1-\beta_2^t}=\frac{0.0698529}{1-{0.999}^3}=\frac{0.0698529}{1-0.997002999}=\frac{0.0698529}{0.002997001}\approx23.3132 </math> | |||
6. Nesterov Adjustment for First Moment: | |||
<math> m\prime_3=\beta_1\widehat{m_3}+\frac{\left(1-\beta_1\right)g_3}{1-\beta_1^t}=0.9\times4.8134+\frac{0.1\times4.6686}{0.271}=4.3321+\frac{0.46686}{0.271}\approx4.3321+1.7227=6.0548 </math> | |||
7. Parameter Update: | |||
<math> \theta_3=\theta_2-\eta\frac{m\prime_3}{\sqrt{\widehat{v_3}}+\epsilon}=4.6686-0.1\times\frac{6.0548}{\sqrt{23.3132}+{10}^{-8}}=4.6686-0.1\times\frac{6.0548}{4.8284}=4.6686-0.1\times1.2547=4.6686-0.12547=4.5431 </math> | |||
After three iterations, the parameter values have been updated as follows: | |||
<math> \theta_1=4.81 </math> | |||
<math> \theta_2=4.6686 </math> | |||
<math> \theta_3=4.5431 </math> | |||
The parameter <math> \theta </math> is gradually moving towards the global minimum at <math> \theta=0 </math>, demonstrating how the Nadam optimizer adjusts the parameters efficiently. | |||
=== Linear Regression Task === | |||
A simple linear regression task is demonstrated to predict house prices based on size. The hypothesis function, cost function, and optimization problem are defined, and numerical calculations are provided along with plots to visualize Nadam on the dataset. | |||
''''' Dataset ''''' | |||
Consider the following dataset representing the size (in square feet) and price (in thousands of dollars) of several houses: | |||
{| class="wikitable" | |||
|- | |||
| Size (sq ft) || 50 || 60 || 70 || 80 || 90 || 100 || 110 || 120 || 130 || 140 || 150 | |||
|- | |||
| Price ($K) || 150 || 180 || 200 || 240 || 300 || 330 || 360 || 400 || 450 || 500 || 550 | |||
|} | |||
The aim is to model the relationship between the size of a house and its price using a linear hypothesis function: | |||
<math> f_\theta\left(x\right)=\theta_0+\theta_1x </math> | |||
The cost function measures the discrepancy between the predicted prices and the actual prices. Using the Mean Squared Error (MSE) as the cost function: | |||
<math> J\left(\theta\right)=\frac{1}{2}\sum_{i}^{n}\left(f_\theta\left(x_i\right)-y_i\right)^2 </math> | |||
The goal is to find the optimal parameters <math> \theta=\left(\theta_0,\theta_1\right) </math> that minimize the cost function: | |||
<math> \mathrm{argmin}_{\mathrm{\theta}}\frac{1}{n}\sum_i^{n}\left(f_\theta\left(x_i\right)-y_i\right)^2 </math> | |||
To minimize the cost function using gradient-based optimization, compute the partial derivatives with respect to <math> \theta_0 </math> and <math> \theta_1 </math>: | |||
<math> \frac{\partial J\left(\theta\right)}{\partial\theta_0}=\sum_{i=1}^{n}\left(f_\theta\left(x_i\right)-y_i\right) </math> | |||
<math> \frac{\partial J\left(\theta\right)}{\partial\theta_1}=\sum_{i=1}^{n}{\left(f_\theta\left(x_i\right)-y_i\right)x_i} </math> | |||
''''' Numerical Example ''''' | |||
Considering only the first few data points to simplify the calculations: | |||
{| class="wikitable" | |||
|- | |||
| Size (sq ft) || 50 || 60 || 70 || 80 | |||
|- | |||
| Price ($K) || 150 || 180 || 200 || 240 | |||
|} | |||
''''' Initial Conditions ''''' | |||
Assume <math> \theta_0=0, \theta_1=0, \eta=0.01, \beta_1=0.9, \beta_2=0.999, \epsilon={10}^{-8} </math>. | |||
Initialize <math> m_0^{\left(\theta_0\right)}=0, m_0^{\left(\theta_1\right)}=0, v_0^{\left(\theta_0\right)}=0, v_0^{\left(\theta_1\right)}=0, t=0 </math>. | |||
'''Iteration 1''' | |||
1. Increment time step: | |||
<math> t \leftarrow t+1 = 1 </math> | |||
2. Compute predictions and residuals: | |||
<math> f_{\theta}(x_i)=\theta_0+\theta_1x_i=0 </math> | |||
Residuals: | |||
<math> f_{\theta}(x_i)-y_i=(-150),(-180),(-200),(-240) </math> | |||
3. Compute gradients: | |||
<math> \frac{\partial J}{\partial \theta_0}=\sum_{i=1}^{4}(f_{\theta}(x_i)-y_i)=(-150)+(-180)+(-200)+(-240)=-770 </math> | |||
<math> \frac{\partial J}{\partial \theta_1}=\sum_{i=1}^{4}(f_{\theta}(x_i)-y_i)x_i=(-150\cdot50)+(-180\cdot60)+(-200\cdot70)+(-240\cdot80) </math> | |||
Compute each product: | |||
<math> -150\cdot50=-7500, ; -180\cdot60=-10800, ; -200\cdot70=-14000, ; -240\cdot80=-19200 </math> | |||
Summation: <math> -7500-10800-14000-19200=-51500 </math> | |||
Thus, <math> \frac{\partial J}{\partial \theta_1}=-51500 </math> | |||
4. Update biased first moments: | |||
<math> m_1^{(\theta_0)}=\beta_1 m_0^{(\theta_0)}+(1-\beta_1)\frac{\partial J}{\partial \theta_0}=0.9\cdot0+0.1\cdot(-770)=-77 </math> | |||
<math> m_1^{(\theta_1)}=\beta_1 m_0^{(\theta_1)}+(1-\beta_1)\frac{\partial J}{\partial \theta_1}=0.9\cdot0+0.1\cdot(-51500)=-5150 </math> | |||
5. Update biased second moments: | |||
<math> v_1^{(\theta_0)}=\beta_2 v_0^{(\theta_0)}+(1-\beta_2)(-770)^2=0.999\cdot0+0.001\cdot592900=592.9 </math> | |||
<math> v_1^{(\theta_1)}=\beta_2 v_0^{(\theta_1)}+(1-\beta_2)(-51500)^2=0.999\cdot0+0.001\cdot2652250000=2,652,250 </math> | |||
6. Compute bias-corrected moments: | |||
<math> \hat{m}_1^{(\theta_0)}=\frac{m_1^{(\theta_0)}}{1-\beta_1^1}=\frac{-77}{1-0.9}=\frac{-77}{0.1}=-770 </math> | |||
<math> \hat{m}_1^{(\theta_1)}=\frac{m_1^{(\theta_1)}}{1-\beta_1^1}=\frac{-5150}{0.1}=-51500 </math> | |||
<math> \hat{v}_1^{(\theta_0)}=\frac{v_1^{(\theta_0)}}{1-\beta_2^1}=\frac{592.9}{1-0.999}=592.9/0.001=592900 </math> | |||
<math> \hat{v}_1^{(\theta_1)}=\frac{v_1^{(\theta_1)}}{1-0.999}=2,652,250/0.001=2,652,250,000 </math> | |||
7. Nesterov adjustment: | |||
For Nadam, incorporate Nesterov momentum by adding <math> \frac{(1-\beta_1)\partial J/\partial \theta}{1-\beta_1^t} </math> to <math> \beta_1\hat{m}_t </math>. | |||
For <math> \theta_0 </math>: | |||
<math> m{\prime}_1(\theta_0)=\beta_1\hat{m}_1^{(\theta_0)}+\frac{(1-\beta_1)\frac{\partial J}{\partial \theta_0}}{1-\beta_1^1}=0.9\cdot(-770)+\frac{0.1\cdot(-770)}{0.1}=(-693)+(-770)=-1463 </math> | |||
For <math> \theta_1 </math>: | |||
<math> m{\prime}_1(\theta_1)=0.9\cdot(-51500)+\frac{0.1\cdot(-51500)}{0.1}=(-46350)+(-51500)=-97850 </math> | |||
8. Parameter update: | |||
<math> \theta_0 \leftarrow \theta_0 - \eta \frac{m{\prime}_1(\theta_0)}{\sqrt{\hat{v}_1^{(\theta_0)}}+\epsilon}=0 - 0.01\frac{-1463}{\sqrt{592900}+10^{-8}} </math> | |||
<math> \sqrt{592900}\approx770 </math>. Thus: | |||
<math> \theta_0 \leftarrow 0 - 0.01\frac{-1463}{770}=0 - 0.01(-1.9)=0 + 0.019=0.019 </math> | |||
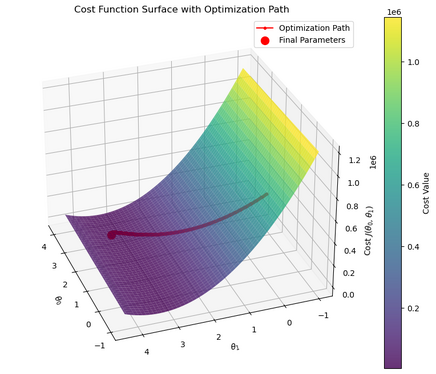
[[File:Cost surface.png|thumb|436x436px|Cost surface trajectory for the linear regression task using NADAM]] | |||
<math> \theta_1 \leftarrow \theta_1 - 0.01\frac{-97850}{\sqrt{2,652,250,000}+10^{-8}} </math> | |||
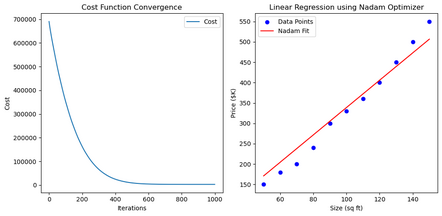
[[File:Loss regression.png|thumb|442x442px|Cost function convergence and the final linear fit for the dataset]] | |||
<math> \sqrt{2,652,250,000}\approx 51500 </math>. Thus: | |||
<math> \theta_1 \leftarrow 0 - 0.01\frac{-97850}{51500}=0 - 0.01(-1.9)=0.019 </math> | |||
After one iteration, the parameters have moved closer to values that reduce the cost. | |||
== Applications == | |||
Nadam’s integration of adaptive moment estimation with Nesterov accelerated gradients makes it a powerful tool for both convex and non-convex optimization problems, particularly in training complex neural networks. It has been widely applied in diverse domains: for instance, Nadam has been used to optimize convolutional neural networks (CNNs) in tasks like image denoising <ref> L. Fan and Z. Long, “Optimization of Nadam algorithm for image denoising based on convolutional neural network,” in 2020 7th International Conference on Information Science and Control Engineering (ICISCE), Dec. 2020, pp. 957–961. doi: 10.1109/ICISCE50968.2020.00197.</ref> and human chromosome classification <ref> D. Menaka and S. G. Vaidyanathan, “Chromenet: a CNN architecture with comparison of optimizers for classification of human chromosome images,” Multidimens. Syst. Signal Process., vol. 33, no. 3, pp. 747–768, Sep. 2022, doi: 10.1007/s11045-022-00819-x.</ref>, demonstrating enhanced performance and faster convergence. In the context of time-series prediction, Nadam has been employed to optimize Long Short-Term Memory (LSTM) networks for predicting pressure in coal mining working faces, where they showed the Nadam-LSTM model outperforms LSTM model with basic gradient descent optimization <ref> J. Lu, Z. Liu, W. Zhang, J. Zheng, and C. Han, “Pressure Prediction Study of Coal Mining Working Face Based on Nadam-LSTM,” IEEE Access, vol. 11, pp. 83867–83880, 2023, doi: 10.1109/ACCESS.2023.3302516.</ref>. Furthermore, it has shown effectiveness in text sentiment analysis by training LSTMs, where its combination with L2 regularization achieved higher accuracy in fewer epochs <ref> J. Wang and Z. Cao, “Chinese text sentiment analysis using LSTM network based on L2 and Nadam,” in 2017 IEEE 17th International Conference on Communication Technology (ICCT), Oct. 2017, pp. 1891–1895. doi: 10.1109/ICCT.2017.8359958 </ref>. Nadam’s robustness and adaptability have led to its integration into major deep learning libraries such as TensorFlow [https://www.tensorflow.org/api_docs/python/tf/keras/optimizers/Nadam] and PyTorch [https://pytorch.org/docs/stable/generated/torch.optim.NAdam.html?utm_source=chatgpt.com], making it a readily accessible optimizer for a wide range of machine learning tasks. | |||
== Conclusion == | |||
Nadam combines the adaptive learning rate adjustment of Adam with the anticipatory gradient updates of Nesterov momentum, making it a powerful extension of Adam. By incorporating the Nesterov approach, Nadam calculates gradients at a projected future position, which allows for more responsive and accurate updates, improving convergence speed and stability. This makes Nadam a robust tool for optimization tasks, particularly for training deep neural networks in both convex and non-convex settings. While Nadam has been effectively applied in areas like image classification, time-series prediction, and natural language processing, its suitability for specific problem types remains a topic for further exploration and research. Overall, Nadam offers several advantages, including faster convergence, improved handling of noisy gradients, and better generalization compared to traditional methods like SGD, Momentum, or Adam. These strengths make Nadam a versatile and reliable optimizer in modern machine learning applications. | |||
== References == | |||
<references/> | |||
Latest revision as of 12:31, 15 December 2024
Author: Vinamr Jain (vj89) (ChemE 6800 Fall 2024)
Stewards: Nathan Preuss, Wei-Han Chen, Tianqi Xiao, Guoqing Hu
Introduction
Nesterov-accelerated Adaptive Moment Estimation (Nadam) is an optimization algorithm introduced by Timothy Dozat in his 2016 paper, “Incorporating Nesterov Momentum into Adam” [1]. Nadam enhances the Adaptive Moment Estimation (Adam) optimizer by integrating Nesterov momentum, aiming to improve convergence speed and performance in training deep learning models. This algorithm has been applied across various domains, including computer vision and natural language processing, to optimize neural network training. Gradient descent optimization algorithms are fundamental tools in machine learning, often employed as black-box optimizers to minimize loss functions by iteratively adjusting model parameters. Gradient Descent updates parameters by following the negative gradient of the loss function to seek a minimum, but can be slow to converge, especially in regions with flat or elongated curvatures [2]. Several variants address these challenges. Momentum accelerates convergence by accumulating a decaying sum of past gradients, helping navigate ravines and reducing oscillations [1]. Nesterov’s Accelerated Gradient (NAG), also known as Nesterov momentum, improves upon Momentum by calculating the gradient at a projected future position, often resulting in faster convergence. RMSprop adapts learning rates for each parameter individually and normalizes gradients by a decaying average of recent magnitudes, effectively handling non-stationary objectives [3]. Adaptive Moment Estimation (Adam) [4] combines the benefits of Momentum and adaptive learning rates, computing individual adaptive rates based on first and second moments of gradients. However, Adam may sometimes converge to suboptimal solutions due to its adaptive learning rate mechanism [3] and can slow down before reaching global optima [2]. Nadam extends Adam by incorporating Nesterov momentum, evaluating the gradient at a projected future parameter position and improving convergence speed and accuracy.
Background
Gradient Descent is a first-order iterative optimization algorithm used to find a local minimum of a differentiable function. The parameter update rule at iteration is: Where denotes the parameters vector at iteration , is the learning rate, and is the gradient of the cost function with respect to at iteration . Momentum accelerates Gradient Descent by accumulating an exponentially decaying moving average of past gradients. This accelerates gradient descent along stable gradient directions and slows it in oscillating directions [1].
Here in addition to the gradient component, there’s an additional term , the momentum vector, and is the momentum coefficient. Nesterov Momentum improves upon standard Momentum by calculating the gradient at the anticipated future position, leading to a more responsive update.
Alternatively, one can apply the current look-ahead momentum vector directly to update the current parameters:
AdaGrad (Adaptive Gradient Algorithm) adapts the learning rate for each parameter individually by scaling it inversely proportional to the square root of the sum of all historical squared values of the gradients. This method is particularly useful for dealing with sparse data [3].
is the accumulated sum of squared gradients up to time , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon } is a small constant for numerical stability (e.g., Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-8} } ). AdaGrad effectively scales down the learning rate for parameters associated with frequently occurring features, allowing for larger updates for infrequent features [1].
RMSprop (Root Mean Square Propagation) is an optimization algorithm that builds upon AdaGrad by modifying the way it accumulates squared gradients. While AdaGrad accumulates all past squared gradients, leading to a continually decreasing learning rate, RMSprop introduces a decay parameter to the accumulated squared gradients Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_t } . This parameterization prevents the learning rate from diminishing too quickly.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_t=\gamma v_{t-1}+\left(1-\gamma\right)\left[\nabla_\theta J\left(\theta_t\right)\right]^2 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_{t+1}=\theta_t-\eta\frac{\nabla_\theta J\left(\theta_t\right)}{\sqrt{v_t}+\epsilon} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma } is the decay rate (typically Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma=0.9 } ). By introducing the decay parameter in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_t } term, RMSprop limits the influence of older gradients, ensuring that the algorithm adapts quickly to the most recent gradients.
Adam (Adaptive Moment Estimation) is an optimization algorithm that combines ideas from both Momentum and RMSprop. It extends RMSprop by not only adapting the learning rates per parameter but also incorporating momentum by using an exponentially decaying average of past gradients (first moment). Adam is designed to work well with sparse gradients and noisy problems, which are common in training deep neural networks.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_t=\beta_1m_{t-1}+\left(1-\beta_1\right)\nabla_\theta J\left(\theta_t\right) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_t=\beta_2v_{t-1}+\left(1-\beta_2\right)\left[\nabla_\theta J\left(\theta_t\right)\right]^2 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_t } is the first moment estimate (exponentially decaying average of past gradients), Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_t } is the second moment estimate (exponentially decaying average of past squared gradients), and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_1 } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_2 } are the exponential decay rates for the moment estimates (commonly Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_1=0.9, \beta_2=0.999 } ).
As Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_t } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_t } are initialized at zero vectors, they are biased towards zero, especially during the initial time steps and particularly when the decay rates are close to one (i.e., Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_1, \beta_2\approx1 } ). This bias can slow down the convergence of the algorithm because the moment estimates underestimate the true mean and variance of the gradients. To counteract these biases, the authors of Adam introduced bias-corrected moment estimates:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{m_t}=\frac{m_t}{1-\beta_1^t} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{v_t}=\frac{v_t}{1-\beta_2^t} }
The denominators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1-\beta_1^t } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1-\beta_2^t } approach 1 as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t } increases, reducing the impact of the bias over time. The bias correction compensates for the initialization at zero, ensuring that the moment estimates are unbiased. The parameters are then updated using the bias-corrected moment estimates:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_{t+1}=\theta_t-\eta\frac{\widehat{m_t}}{\sqrt{\widehat{v_t}}+\epsilon} }
Algorithm
Nadam modifies the parameter update step of Adam by integrating the Nesterov accelerated gradient. In Adam, the update relies solely on the bias-corrected first moment estimate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{m_t} } . Nadam modifies the parameter update step of Adam by integrating the Nesterov accelerated gradient. In Adam, the update relies solely on the bias-corrected first moment estimate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{m_t} } . Nadam, however, adjusts this estimate by adding a term that accounts for the current gradient, effectively looking ahead to where the parameters are heading. This adjustment is similar to the Nesterov momentum in NAG, which computes the gradient at the approximate future position of the parameters. Firstly, consider the bias-corrected first moment Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{m_t} } using the definition of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_t } [3]
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{m_t}=\frac{m_t}{1-\beta_1^t}=\frac{\beta_1m_{t-1}+\left(1-\beta_1\right)g_t}{1-\beta_1^t} }
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_t=\nabla_\theta J\left(\theta_t\right) } . The update rule of Adam can be rewritten as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_{t+1}=\theta_t-\frac{\eta}{\left(\sqrt{\widehat{v_t}}+\epsilon\right)}\left[\frac{\beta_1m_{t-1}}{\left(1-\beta_1^t\right)}+\frac{\left(1-\beta_1\right)g_t}{\left(1-\beta_1^t\right)}\right] }
Recognizing that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\beta_1m_{t-1}}{1-\beta_1^t} } is the bias-corrected estimate of the momentum vector from the previous time step, let’s denote:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{m_{t-1}}=\frac{m_{t-1}}{1-\beta_1^{t-1}} }
However, since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_1^{t-1} } is close to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_1^t } for large Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t } , it can be approximated as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\beta_1m_{t-1}}{1-\beta_1^t}\approx\beta_1\widehat{m_{t-1}} } Thus, the update rule becomes:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_{t+1}=\theta_t-\eta\frac{\beta_1\widehat{m_{t-1}}+\frac{\left(1-\beta_1\right)g_t}{1-\beta_1^t}}{\sqrt{\widehat{v_t}}+\epsilon} }
This form resembles the momentum term in Nesterov Accelerated Gradient (NAG). To incorporate Nesterov momentum into Adam, the previous bias-corrected momentum estimate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{m_{t-1}} } is replaced with the current estimate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{m_t} } . This aligns with the NAG approach of using the look-ahead momentum vector for updating parameters.
The Nadam update rule becomes:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_{t+1}=\theta_t-\eta\frac{\beta_1\widehat{m_t}+\frac{\left(1-\beta_1\right)g_t}{1-\beta_1^t}}{\sqrt{\widehat{v_t}}+\epsilon} }
By combining the bias-corrected first moment estimate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{m_t} } and the current gradient Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_t } , weighted appropriately, Nadam aims to improve the responsiveness of the optimizer to recent gradient information, potentially enhancing convergence speed.
Pseudocode
The pseudocode for Nadam is as follows:
Algorithm Nadam Optimization Input: Initial parameters Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_0 } , learning rate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta } , decay rates Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_1 } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_2 } , small constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon }
Initialize Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_0\gets0,v_0\gets0,t\gets0 }
While not converged do
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t\ \gets t\ +\ 1 }
Compute gradient: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_t=\nabla_\theta J\left(\theta_{t-1}\right) }
Update biased first moment: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_t\gets\beta_1\cdot m_{t-1}+\left(1-\beta_1\right)\cdot g_t }
Update biased second moment: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_t\gets\beta_2\cdot v_{t-1}+\left(1-\beta_2\right)\cdot g_t^2 }
Bias correction: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{m_t}\gets\frac{m_t}{1-\beta_1^t}, \widehat{v_t}\gets\frac{v_t}{1-\beta_2^t} }
Nesterov adjustment: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m'_t \gets \beta_1 \cdot \widehat{m_t} + \frac{\left(1 - \beta_1\right) \cdot g_t}{1 - \beta_1^t} }
Update parameters: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_t \gets \theta_{t-1} - \eta \cdot \frac{m'_t}{\sqrt{\widehat{v_t}} + \epsilon} }
Output: Optimized parameters Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_t }
Numerical Examples
This section provides numerical examples to illustrate how the Nadam algorithm operates. We choose a simple quadratic function to make the calculations straightforward and easy to follow, and then we demonstrate the numerical calculations for a linear regression task.
Minimizing a Quadratic Function
Consider the cost function: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J\left(\theta\right)=\frac{1}{2}\theta^2 } which has its global minimum at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta=0 } . The aim is to minimize this function using the Nadam optimizer, starting from an initial parameter value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_0=5 } .
The hyperparameters are set as follows: learning rate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta=0.1 } , exponential decay rates Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_1,\beta_2=0.9 } , numerical stability constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon={10}^{-8} } , and initialize the first and second moment estimates and the time step as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_0=0, v_0=0, t=0 } .
Iteration 1
1. Time Step Update:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t\ \gets t\ +\ 1\ =\ 1 }
2. Compute Gradient at Current Parameter:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_1=\nabla_\theta J\left(\theta_0\right)=\theta_0=5 }
3. Update Biased First Moment Estimate:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_1=\beta_1m_0+\left(1-\beta_1\right)g_1=0.9\times0+0.1\times5=0.5 }
4. Update Biased Second Moment Estimate:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_1=\beta_2v_0+\left(1-\beta_2\right)g_1^2=0.999\times0+0.001\times25=0.025 }
5. Compute Bias-Corrected Estimates:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{m_1}=\frac{m_1}{1-\beta_1^t}=\frac{0.5}{1-{0.9}^1}=\frac{0.5}{0.1}=5 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{v_1}=\frac{v_1}{1-\beta_2^t}=\frac{0.025}{1-{0.999}^1}=\frac{0.025}{0.001}=25 }
6. Nesterov Adjustment for First Moment:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\prime_1=\beta_1\widehat{m_1}+\frac{\left(1-\beta_1\right)g_1}{1-\beta_1^t}=0.9\times5+\frac{0.1\times5}{0.1}=4.5+5=9.5 }
7. Parameter Update:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_1=\theta_0-\eta\frac{m\prime_1}{\sqrt{\widehat{v_1}}+\epsilon}=5-0.1\times\frac{9.5}{\sqrt{25}+{10}^{-8}}=5-0.1\times\frac{9.5}{5}=5-0.1\times1.9=5-0.19=4.81 }
Iteration 2
1. Time Step Update:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t\ \gets t\ +\ 1\ =\ 2 }
2. Compute Gradient at Current Parameter:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_2=\nabla_\theta J\left(\theta_1\right)=\theta_1=4.81 }
3. Update Biased First Moment Estimate:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_2=\beta_1m_1+\left(1-\beta_1\right)g_2=0.9\times0.5+0.1\times4.81=0.45+0.481=0.931 }
4. Update Biased Second Moment Estimate:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_2=\beta_2v_1+\left(1-\beta_2\right)g_2^2=0.999\times0.025+0.001\times\left(4.81\right)^2=0.024975+0.001\times23.1361=0.024975+0.0231361=0.0481111 }
5. Compute Bias-Corrected Estimates:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{m_2}=\frac{m_2}{1-\beta_1^t}=\frac{0.931}{1-{0.9}^2}=\frac{0.931}{1-0.81}=\frac{0.931}{0.19}\approx4.9005 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{v_2}=\frac{v_2}{1-\beta_2^t}=\frac{0.0481111}{1-{0.999}^2}=\frac{0.0481111}{1-0.998001}=\frac{0.0481111}{0.001999}\approx24.0696 }
6. Nesterov Adjustment for First Moment:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\prime_2=\beta_1\widehat{m_2}+\frac{\left(1-\beta_1\right)g_2}{1-\beta_1^t}=0.9\times4.9005+\frac{0.1\times4.81}{0.19}=4.41045+\frac{0.481}{0.19}\approx4.41045+2.5316=6.9421 }
7. Parameter Update:
Iteration 3
1. Time Step Update:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t\ \gets t\ +\ 1\ =\ 3 }
2. Compute Gradient at Current Parameter:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_3=\nabla_\theta J\left(\theta_2\right)=\theta_2=4.6686 }
3. Update Biased First Moment Estimate:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_3=\beta_1m_2+\left(1-\beta_1\right)g_3=0.9\times0.931+0.1\times4.6686=0.8379+0.46686=1.30476 }
4. Update Biased Second Moment Estimate:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_3=\beta_2v_2+\left(1-\beta_2\right)g_3^2=0.999\times0.0481111+0.001\times\left(4.6686\right)^2=0.048063+0.001\times21.7899=0.048063+0.0217899=0.0698529 }
5. Compute Bias-Corrected Estimates:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{m_3}=\frac{m_3}{1-\beta_1^t}=\frac{1.30476}{1-{0.9}^3}=\frac{1.30476}{1-0.729}=\frac{1.30476}{0.271}\approx4.8134 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{v_3}=\frac{v_3}{1-\beta_2^t}=\frac{0.0698529}{1-{0.999}^3}=\frac{0.0698529}{1-0.997002999}=\frac{0.0698529}{0.002997001}\approx23.3132 }
6. Nesterov Adjustment for First Moment:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\prime_3=\beta_1\widehat{m_3}+\frac{\left(1-\beta_1\right)g_3}{1-\beta_1^t}=0.9\times4.8134+\frac{0.1\times4.6686}{0.271}=4.3321+\frac{0.46686}{0.271}\approx4.3321+1.7227=6.0548 }
7. Parameter Update:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_3=\theta_2-\eta\frac{m\prime_3}{\sqrt{\widehat{v_3}}+\epsilon}=4.6686-0.1\times\frac{6.0548}{\sqrt{23.3132}+{10}^{-8}}=4.6686-0.1\times\frac{6.0548}{4.8284}=4.6686-0.1\times1.2547=4.6686-0.12547=4.5431 }
After three iterations, the parameter values have been updated as follows:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_1=4.81 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_2=4.6686 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_3=4.5431 }
The parameter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta } is gradually moving towards the global minimum at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta=0 } , demonstrating how the Nadam optimizer adjusts the parameters efficiently.
Linear Regression Task
A simple linear regression task is demonstrated to predict house prices based on size. The hypothesis function, cost function, and optimization problem are defined, and numerical calculations are provided along with plots to visualize Nadam on the dataset.
Dataset
Consider the following dataset representing the size (in square feet) and price (in thousands of dollars) of several houses:
| Size (sq ft) | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 |
| Price ($K) | 150 | 180 | 200 | 240 | 300 | 330 | 360 | 400 | 450 | 500 | 550 |
The aim is to model the relationship between the size of a house and its price using a linear hypothesis function: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_\theta\left(x\right)=\theta_0+\theta_1x }
The cost function measures the discrepancy between the predicted prices and the actual prices. Using the Mean Squared Error (MSE) as the cost function:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J\left(\theta\right)=\frac{1}{2}\sum_{i}^{n}\left(f_\theta\left(x_i\right)-y_i\right)^2 }
The goal is to find the optimal parameters Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta=\left(\theta_0,\theta_1\right) } that minimize the cost function:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{argmin}_{\mathrm{\theta}}\frac{1}{n}\sum_i^{n}\left(f_\theta\left(x_i\right)-y_i\right)^2 }
To minimize the cost function using gradient-based optimization, compute the partial derivatives with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_0 } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_1 } :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial J\left(\theta\right)}{\partial\theta_0}=\sum_{i=1}^{n}\left(f_\theta\left(x_i\right)-y_i\right) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial J\left(\theta\right)}{\partial\theta_1}=\sum_{i=1}^{n}{\left(f_\theta\left(x_i\right)-y_i\right)x_i} }
Numerical Example
Considering only the first few data points to simplify the calculations:
| Size (sq ft) | 50 | 60 | 70 | 80 |
| Price ($K) | 150 | 180 | 200 | 240 |
Initial Conditions
Assume Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_0=0, \theta_1=0, \eta=0.01, \beta_1=0.9, \beta_2=0.999, \epsilon={10}^{-8} } . Initialize Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_0^{\left(\theta_0\right)}=0, m_0^{\left(\theta_1\right)}=0, v_0^{\left(\theta_0\right)}=0, v_0^{\left(\theta_1\right)}=0, t=0 } .
Iteration 1
1. Increment time step:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t \leftarrow t+1 = 1 }
2. Compute predictions and residuals:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{\theta}(x_i)=\theta_0+\theta_1x_i=0 }
Residuals:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{\theta}(x_i)-y_i=(-150),(-180),(-200),(-240) }
3. Compute gradients:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial J}{\partial \theta_0}=\sum_{i=1}^{4}(f_{\theta}(x_i)-y_i)=(-150)+(-180)+(-200)+(-240)=-770 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial J}{\partial \theta_1}=\sum_{i=1}^{4}(f_{\theta}(x_i)-y_i)x_i=(-150\cdot50)+(-180\cdot60)+(-200\cdot70)+(-240\cdot80) }
Compute each product:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -150\cdot50=-7500, ; -180\cdot60=-10800, ; -200\cdot70=-14000, ; -240\cdot80=-19200 }
Summation: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -7500-10800-14000-19200=-51500 }
Thus, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial J}{\partial \theta_1}=-51500 }
4. Update biased first moments:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_1^{(\theta_0)}=\beta_1 m_0^{(\theta_0)}+(1-\beta_1)\frac{\partial J}{\partial \theta_0}=0.9\cdot0+0.1\cdot(-770)=-77 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_1^{(\theta_1)}=\beta_1 m_0^{(\theta_1)}+(1-\beta_1)\frac{\partial J}{\partial \theta_1}=0.9\cdot0+0.1\cdot(-51500)=-5150 }
5. Update biased second moments:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_1^{(\theta_0)}=\beta_2 v_0^{(\theta_0)}+(1-\beta_2)(-770)^2=0.999\cdot0+0.001\cdot592900=592.9 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_1^{(\theta_1)}=\beta_2 v_0^{(\theta_1)}+(1-\beta_2)(-51500)^2=0.999\cdot0+0.001\cdot2652250000=2,652,250 }
6. Compute bias-corrected moments:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{m}_1^{(\theta_0)}=\frac{m_1^{(\theta_0)}}{1-\beta_1^1}=\frac{-77}{1-0.9}=\frac{-77}{0.1}=-770 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{m}_1^{(\theta_1)}=\frac{m_1^{(\theta_1)}}{1-\beta_1^1}=\frac{-5150}{0.1}=-51500 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{v}_1^{(\theta_0)}=\frac{v_1^{(\theta_0)}}{1-\beta_2^1}=\frac{592.9}{1-0.999}=592.9/0.001=592900 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{v}_1^{(\theta_1)}=\frac{v_1^{(\theta_1)}}{1-0.999}=2,652,250/0.001=2,652,250,000 }
7. Nesterov adjustment:
For Nadam, incorporate Nesterov momentum by adding Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{(1-\beta_1)\partial J/\partial \theta}{1-\beta_1^t} } to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_1\hat{m}_t } .
For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_0 } :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m{\prime}_1(\theta_0)=\beta_1\hat{m}_1^{(\theta_0)}+\frac{(1-\beta_1)\frac{\partial J}{\partial \theta_0}}{1-\beta_1^1}=0.9\cdot(-770)+\frac{0.1\cdot(-770)}{0.1}=(-693)+(-770)=-1463 }
For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_1 } :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m{\prime}_1(\theta_1)=0.9\cdot(-51500)+\frac{0.1\cdot(-51500)}{0.1}=(-46350)+(-51500)=-97850 }
8. Parameter update:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_0 \leftarrow \theta_0 - \eta \frac{m{\prime}_1(\theta_0)}{\sqrt{\hat{v}_1^{(\theta_0)}}+\epsilon}=0 - 0.01\frac{-1463}{\sqrt{592900}+10^{-8}} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{592900}\approx770 } . Thus:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_0 \leftarrow 0 - 0.01\frac{-1463}{770}=0 - 0.01(-1.9)=0 + 0.019=0.019 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_1 \leftarrow \theta_1 - 0.01\frac{-97850}{\sqrt{2,652,250,000}+10^{-8}} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{2,652,250,000}\approx 51500 } . Thus:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_1 \leftarrow 0 - 0.01\frac{-97850}{51500}=0 - 0.01(-1.9)=0.019 }
After one iteration, the parameters have moved closer to values that reduce the cost.
Applications
Nadam’s integration of adaptive moment estimation with Nesterov accelerated gradients makes it a powerful tool for both convex and non-convex optimization problems, particularly in training complex neural networks. It has been widely applied in diverse domains: for instance, Nadam has been used to optimize convolutional neural networks (CNNs) in tasks like image denoising [5] and human chromosome classification [6], demonstrating enhanced performance and faster convergence. In the context of time-series prediction, Nadam has been employed to optimize Long Short-Term Memory (LSTM) networks for predicting pressure in coal mining working faces, where they showed the Nadam-LSTM model outperforms LSTM model with basic gradient descent optimization [7]. Furthermore, it has shown effectiveness in text sentiment analysis by training LSTMs, where its combination with L2 regularization achieved higher accuracy in fewer epochs [8]. Nadam’s robustness and adaptability have led to its integration into major deep learning libraries such as TensorFlow [1] and PyTorch [2], making it a readily accessible optimizer for a wide range of machine learning tasks.
Conclusion
Nadam combines the adaptive learning rate adjustment of Adam with the anticipatory gradient updates of Nesterov momentum, making it a powerful extension of Adam. By incorporating the Nesterov approach, Nadam calculates gradients at a projected future position, which allows for more responsive and accurate updates, improving convergence speed and stability. This makes Nadam a robust tool for optimization tasks, particularly for training deep neural networks in both convex and non-convex settings. While Nadam has been effectively applied in areas like image classification, time-series prediction, and natural language processing, its suitability for specific problem types remains a topic for further exploration and research. Overall, Nadam offers several advantages, including faster convergence, improved handling of noisy gradients, and better generalization compared to traditional methods like SGD, Momentum, or Adam. These strengths make Nadam a versatile and reliable optimizer in modern machine learning applications.
References
- ↑ 1.0 1.1 1.2 1.3 T. Dozat, “Incorporating Nesterov Momentum into Adam”.
- ↑ 2.0 2.1 J. Brownlee, “Gradient Descent Optimization With Nadam From Scratch,” MachineLearningMastery.com. Accessed: Oct. 27, 2024. [Online]. Available: https://www.machinelearningmastery.com/gradient-descent-optimization-with-nadam-from-scratch/
- ↑ 3.0 3.1 3.2 3.3 S. Ruder, “An overview of gradient descent optimization algorithms,” Jun. 15, 2017, arXiv: arXiv:1609.04747. doi: 10.48550/arXiv.1609.04747.
- ↑ D. P. Kingma and J. Ba, “Adam: A Method for Stochastic Optimization,” Jan. 30, 2017, arXiv: arXiv:1412.6980. doi: 10.48550/arXiv.1412.6980.
- ↑ L. Fan and Z. Long, “Optimization of Nadam algorithm for image denoising based on convolutional neural network,” in 2020 7th International Conference on Information Science and Control Engineering (ICISCE), Dec. 2020, pp. 957–961. doi: 10.1109/ICISCE50968.2020.00197.
- ↑ D. Menaka and S. G. Vaidyanathan, “Chromenet: a CNN architecture with comparison of optimizers for classification of human chromosome images,” Multidimens. Syst. Signal Process., vol. 33, no. 3, pp. 747–768, Sep. 2022, doi: 10.1007/s11045-022-00819-x.
- ↑ J. Lu, Z. Liu, W. Zhang, J. Zheng, and C. Han, “Pressure Prediction Study of Coal Mining Working Face Based on Nadam-LSTM,” IEEE Access, vol. 11, pp. 83867–83880, 2023, doi: 10.1109/ACCESS.2023.3302516.
- ↑ J. Wang and Z. Cao, “Chinese text sentiment analysis using LSTM network based on L2 and Nadam,” in 2017 IEEE 17th International Conference on Communication Technology (ICCT), Oct. 2017, pp. 1891–1895. doi: 10.1109/ICCT.2017.8359958













![{\displaystyle v_{t}=v_{t-1}+\left[\nabla _{\theta }J\left(\theta _{t}\right)\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9cd68e279220e3e3d6d9064a2a96e84b55778d7)


