Interior-point method for LP: Difference between revisions
No edit summary |
No edit summary |
||
| Line 30: | Line 30: | ||
=== Problem Formulation === | === Problem Formulation === | ||
[[File:Visualization.png|frame|Visualization of Central Path method in Interior point]] | [[File:Visualization.png|frame|200px|Visualization of Central Path method in Interior point]] | ||
Consider a combination of primal-dual problem below:<br> | Consider a combination of primal-dual problem below:<br> | ||
Revision as of 23:31, 13 November 2020
Authors: Tomas Lopez Lauterio, Rohit Thakur and Sunil Shenoy
Steward: Dr. Fengqi You and Akshay Ajagekar
Introduction
Linear programming problems seeks to optimize linear functions given linear constraints. There are several applications of linear programming including inventory control, production scheduling, transportation optimization and efficient manufacturing processes. Simplex method has been a very popular method to solve these linear programming problems and has served these industries well for a long time. But over the past 40 years, there have been significant number of advances in different algorithms that can be used for solving these types of problems in more efficient ways, especially where the problems become very large scale in terms of variables and constraints. In early 1980s Karmarkar (1984) published a paper introducing interior point methods to solve linear-programming problems. A simple way to look at differences between simplex method and interior point method is that a simplex method moves along the edges of a polytope towards a vertex having a lower value of the cost function, whereas an interior point method begins its iterations inside the polytope and moves towards the lowest cost vertex without regard for edges. This approach reduces the number of iterations needed to reach that vertex, thereby reducing computational time needed to solve the problem.
Lagrange Function
Before getting too deep into description of Interior point method, there are a few concepts that are helpful to understand. First key concept to understand is related to Lagrange function. Lagrange function incorporates the constraints into a modified objective function in such a way that a constrained minimizer (x*) is connected to an unconstrained minimizer {x*, λ*} for the augmented objective function L(x,λ), where the augmentation is achieved with 'p' Lagrange multipliers.
To illustrate this point, if we consider a simple an optimization problem:
minimize f(x)
subject to: A·x = b, where A ε Rpxn is assumed to have a full row rank
Lagrange function can be laid out as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L(x, \lambda ) = f(x) - \sum_{i=1}^{p}\lambda _{i}\cdot a_{i}(x)) }
where, 'λ' introduced in this equation is called Lagrange Multiplier.
Newton's Method
Another key concept to understand is regarding solving linear and non-linear equations using Newton's methods.
Assume you have an unconstrained minimization problem in the form:
minimize g(x) , where g(x) is a real valued function with n variables.
A local minimum for this problem will satisfy the following system of equations:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left [ \frac{\partial g(x)}{\partial x_{1}} ..... \frac{\partial g(x)}{\partial x_{n}}\right ]^{T} = \left [ 0 ... 0 \right ]}
The Newton's iteration looks like:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^{k+1} = x^{k} - \left [ \nabla ^{2} g(x^{k}) \right ]^{-1}\cdot \nabla g(x^{k})}
Theory and algorithm
We first start forming a primal-dual pair of linear programs and use the "Lagrangian function" and "Barrier function" methods to convert the constrained problems into unconstrained problems. These unconstrained problems are then solved using Newton's method as shown above.
Problem Formulation
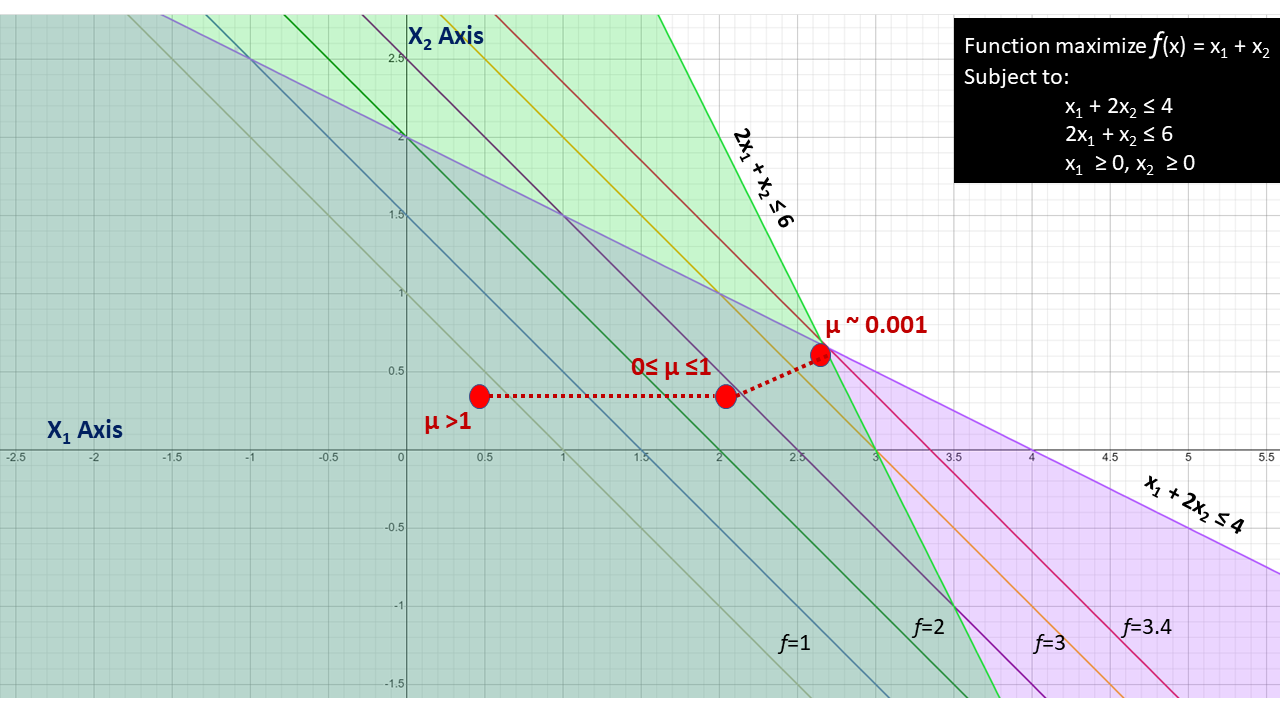
Consider a combination of primal-dual problem below:
(Primal Problem formulation)
→ minimize Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c^{T}x }
Subject to: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ax = b }
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \geq 0 }
.......................................(1)
(Dual Problem formulation)
→ maximize Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b^{T}y }
Subject to: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^{T}y + \lambda = c }
and </math> \lambda \geq 0 </math> ...................(2)
'λ' vector introduced represents the slack variables.
Now we use the "Logarithmic Barrier" function and form 2 Lagrangian equations for primal and dual forms mentioned above:
Lagrange function for Primal : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{p}(x,y) = c^{T}\cdot x + \mu \cdot \sum_{j=1}^{n}log(x_{j}) - y^{T}\cdot (Ax - b) }
......................................(3)
Lagrange function for Dual : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{d}(x,y,\lambda ) = b^{T}\cdot y + \mu \cdot \sum_{j=1}^{n}log(\lambda _{j}) - x^{T}\cdot (A^{T}y -\lambda - c) }
.........(4)
Taking the partial derivatives of Lp and Ld with respect to variables 'x', 'λ' , 'y', and forcing these terms to zero, we get the following equations:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ax = b }
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \geq 0 }
..........................................(5)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^{T}y + \lambda = c }
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda \geq 0 }
.......................(6)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{j}\cdot \lambda _{j} = \mu }
for j= 1,2,.......n .....................(7)
where, μ is strictly positive scaler parameter. For each μ > 0, the vectors in the set {x(μ), y(μ), λ(μ)} satisfying equations (5), (6) and (7), can we viewed as set of points in Rn, Rp, Rn such that when 'μ' varies, the corresponding points form a set of trajectories called "Central Path". THe central path lies in the "Interior" of the feasible regions.
Let us define the following:
X = Diagonal (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{1}^{0}, .... x_{n}^{0} }
)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda }
= Diagonal (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda _{1}^{0}, .... \lambda _{n}^{0} }
)
eT = (1 .....1) as vector of all 1's.
Using these newly defined terms, the equation (7) can be written as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\cdot \lambda \cdot e = \mu \cdot e }
Iterations using Newton's Method
Now we employ the Newton's iterative method to solve the following equations:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ax - b = 0 }
...................................................(8)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^{T}y + \lambda = c }
........................................(9)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\cdot \lambda \cdot e - \mu \cdot e = 0}
..................... (10)
Suppose we start with definition of starting point that lies within feasible region as (x0, y0, λ 0) such that x0>0 and λ 0 >0. Also let us define 2 residual vectors for both the primal and dual equations:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta _{p} = b - A\cdot x^{0} }
.................................(11)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta _{d} = c - A^{0}\cdot y^{0} - \lambda ^{0} }
...............(12)
Applying Newton's Method to solve equations (8) - (12) we get:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} A & 0 & 0\\ 0 & A^{T} & 1\\ \lambda & 0 & X \end{bmatrix} \cdot \begin{bmatrix} \delta _{x}\\ \delta _{y}\\ \delta _{\lambda } \end{bmatrix} = \begin{bmatrix} \delta _{p}\\ \delta _{d}\\ \mu \cdot e - X\cdot \lambda \cdot e \end{bmatrix} }
So a single iteration of Newton's method involves the following equations. For each iteration, we solve for the next value of xk+1, yk+1 and λk+1:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (A\lambda ^{-1}XA^{T})\delta _{y} = b- \mu A\lambda^{-1} + A\lambda ^{-1}X\delta _{d} }
...................(13)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta _{\lambda} = \delta _{d}\cdot A^{T}\delta _{y} }
...................................................(14)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta _{x} = \lambda ^{-1}\left [ \mu \cdot e - X\lambda e -\lambda \delta _{z}\right ] }
.................(15)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha _{p} = min\left \{ \frac{-x_{j}}{\delta _{x_{j}}} \right \} }
for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta x_{j} < 0 }
..... (16)
for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta \lambda_{j} < 0 }
..... (17)
The value of the the following variables for next iteration (k+1) is determined by:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^{k+1} = x^{k} + \alpha _{p}\cdot \delta _{x} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y^{k+1} = y^{k} + \alpha _{d}\cdot \delta _{y} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda^{k+1} = \lambda^{k} + \alpha _{d}\cdot \delta _{\lambda} }
The quantities αp and αd are positive with 0 ≤ αp, αd ≤ 1.
After each iteration of Newton's method, we assess the duality gap that is given by the expression below and compare it against a small value ε
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{c^{T}x^{k}-b^{T}y^{k}}{1+\left | b^{T}y^{k} \right |} \leq \varepsilon }
The value of ε can be chosen to be something small 10-6, which essentially is the permissible duality gap for the problem.
