RMSProp

Author: Jason Huang (SysEn 6800 Fall 2020)

Steward: Allen Yang, Fengqi You

Introduction

RMSProp, so call root mean square propagation, is an optimization algorithm/method dealing with Artificial Neural Network (ANN) for machine learning. It is also a currently developed algorithm compared to the Stochastic Gradient Descent (SGD) algorithm, momentum method. And even one of the foundations of Adam algorithm development. It is an unpublished optimization algorithm, using the adaptive learning rate method, first proposed in the Coursera course “Neural Network for Machine Learning” lecture six by Geoff Hinton. Astonished is that this informally revealed, an unpublished algorithm is intensely famous nowadays.

Theory and Methodology

Artificial Neural Network

Artificial Neural Network can be regarded as the human brain and conscious center of Ariticial Intelligence(AI), presenting the imitation of what the mind will be when human thinking. Scientists are trying to build the concept of ANN close real neurons with their biological ‘parent’.

A single neuron presented as a mathematic function

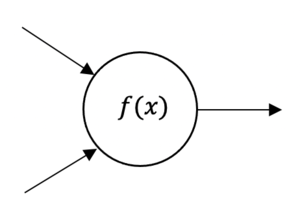
And the function of neurons can be presented as:

$f(x_{1},x_{2})=max(0,w_{1}x_{1}+w_{2}x_{2})$

Where $x_{1},x_{2}$ are two inputs numbers, and function $f(x_{1},x_{2})$ will takes these fixed inputs and create an output of single number. If $w_{1}x_{1}+w_{2}x_{2}$ is greater than 0, the function will return this positive value, or return 0 otherwise. Therefore, the neural network can be replaced as a coupled mathematical function, and its output of a previous function can be used as the next function input.

RProp

RProp, or we call Resilient Back Propagation, is the widely used algorithm for supervised learning with multi-layered feed-forward networks in the past. Besides, its concepts is the foundation of RMSPRop development t. The derivatives equation of error function can be represented as: