Network flow problem

Author: Aaron Wheeler, Chang Wei, Cagla Deniz Bahadir, Ruobing Shui, Ziqiu Zhang (CHEME 6800 Fall 2020)

Steward: Fengqi You, Allen Yang

Introduction:

Network flow problems arise in several key instances and applications within society and have become fundamental problems within computer science, operations research, applied mathematics, and engineering. Developments in the approach to tackle these problems resulted in algorithms that became the chief instruments for solving problems related to large-scale systems and industrial logistics. Spurred by early developments in linear programming, the methods for addressing these extensive problems date back several decades and they evolved over time as the use of digital computing became increasingly prevalent in industrial processes. Historically, the first instance of an algorithmic development for the network flow problem came in 1956, with the network simplex method formulated by George Dantzig [ref]. A variation of the simplex algorithm that revolutionized linear programming, this method leveraged the combinatorial structure inherent to these types of problems and demonstrated incredibly high accuracy [ref]. This method and its variations would go on to define the embodiment of the algorithms and models for the various and distinct network flow problems discussed here.

Theory:

Qualitatively, the network flow problem can be conceptualized as a directed graph which abides by certain flow capacity constraints at its edges and equates the values entering and exiting its vertices at all points besides terminal source and sink terms. The vertices in this problem are the origins, destinations, and intermediate points and are referred to as nodes. The edges are the directional transportation links between these nodes and are referred to as arcs [ref]. Models for network flow problems function as tools for computing the net flow of units along these constrained arcs and between pairs of nodes, and are useful for quantifying logistical interests such as the optimal scheme for the distribution of a product from a plant to it’s consumer constituents. In this scenario, the product departs from the distribution source (origin) and travels through a network of intermediary transition points such as warehouses and fulfillment centers (nodes), before finally reaching the consumer market (destination). Along this journey, the transportation method along the route (arc) may be subjected to certain restraints such as the allowable amount of product carried between points (capacity constraints). The objective function in this case would be to minimize the cost of shipping the product whilst still meeting a specified demand. This exact circumstance is very common in industrial logistics and was the primary motivation for defining and solving the network flow problem [ref]. This case, the transportation problem, was the beginning of a wide assortment of problems defined for network flow by leveraging it’s combinatorial structure in a special-purpose algorithm.

Historically, the classic network flow problems are considered to be the maximum flow problem and the minimum-cost circulation problem, the assignment problem, bipartite matching problem, transportation problem, and the transshipment problem [ref]. The approach to these problems become quite specific based upon the problem’s objective function but can be generalized by the following iterative approach: 1. determining the initial basic feasible solution; 2. checking the optimality conditions (i.e. whether the problem is infeasible, unbounded over the feasible region, optimal solution has been found, etc.); and 3. constructing an improved basic feasible solution if the optimal solution has not been determined [ref].

General Applications

The Assignment Problem:

Various real-life instances of assignment problems exist for optimization, such as assigning a group of people to different tasks, events to halls with different capacities, rewards to a team of contributors, and vacation days to workers. All together, the assignment problem is a bipartite matching problem in the kernel. ^[3] In a classical setting, two types of objects of equal amount are  bijective (i.e. they have one-to-one matching), and this tight constraint ensures a perfect matching. The objective is to minimize the cost or maximize the profit of matching, since different items of two types have distinct affinity.

Figure 1. Classic model of assignment problem

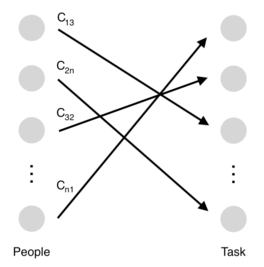
A classic example is as follows: suppose there are n people (set P) to be assigned to n tasks (set T). Every task has to be completed and each task has to be handled by only one person, and cij, usually given by a table, measures the benefits gained by assigning the person i (in P) to the task j (in T). ^[4] The natural objective here is to maximize the overall benefits by devising the optimal assignment pattern. A graph of the general assignment problem and a table of preference are depicted as Figure 1 and Table 1.

Table 1. Table of preference

Benefits	Task 1	Task 2	Task 3	...	Task n
Person 1	0	3	5	...	2
Person 2	2	1	3	...	6
Person 3	1	4	0	...	3
...	...	...	...	...	...
Person n	0	2	3	...	3

Figure 1 can be viewed as a network. The nodes represent people and tasks, and the edges represent potential assignments between a person and a task. Each task can be completed by any person. However, the person that actually ends up being assigned to the task will be the lone individual who is best suited to complete. In the end, the edges with positive flow values will be the only ones represented in the finalized assignment. ^[5]

To approach this problem, the binary variable x_ij is defined as whether the person i is assigned to the task j. If so, x_ij = 1, and x_ij = 0 otherwise.

The concise-form formulation of the problem is as follows ^[3]:

Maximize: $z=\sum _{i=1}^{n}\sum _{j=1}^{n}c_{ij}x_{ij}$

Subject to:

$\sum _{j=1}^{n}x_{ij}=1~~\forall i\in [1,n]$

$\sum _{I=1}^{n}x_{ij}=1~~\forall j\in [1,n]$

$x_{ij}=0~or~1~~\forall i,j\in [1,n]$

The first constraint captures the requirement of assigning each person  to a single task. The second constraint indicates that each task must be done by exactly one person. The objective function sums up the overall benefits of all assignments.

To see the analogy between the assignment problem and the network flow, we can describe each person supplying a flow of 1 unit and each task demanding a flow of 1 unit, with the benefits over all “channels” being maximized. ^[3]

A potential issue lies in the  branching of the network, specifically an instance where a person splits their one unit of flow into multiple tasks and the objective remains maximized. This shortcoming is allowed by the laws that govern the network flow model, but are unfeasible in real-life instances. Fortunately, since the network simplex method only involves addition and subtraction of a single edge while transferring the basis, which is served by the spanning tree of the flow graph, if the supply (the number of people here) and the demand (the number of tasks here) in the constraints are integers, the solved variables will be automatically integers even if it is not explicitly stated in the problem. This is called the integrality of the network problem, and it certainly applies to the assignment problem. ^[6]

The Shortest-Path Problem

The shortest-path problem can be defined as finding the path that yields the shortest total distance between the origin and the destination. Each possible stop is a node and the paths between these nodes are edges incident to these nodes, where the path distance becomes the weight of the edges. In addition to being the most common and straightforward application for finding the shortest path, this model is also used in various applications depending on the definition of nodes and edges. ^[3] For example, when each node represents a different object and the edge specifies the cost of replacement, the equipment replacement problem is derived. Moreover, when each node represents a different project and the edge specifies the relative priority, the model becomes a project scheduling problem.

Figure 2. General form of shortest-path problem

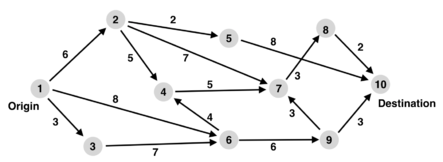
A graph of the general shortest-path problem is depicted as Figure 2:

In the general form of the shortest-path problem, the variable x_ij represents whether the edge (i, j) is active (i.e. with a positive flow), and the parameter c_ij (e.g. c₁₂ = 6) defines the distance of the edge (i, j). The general problem is formulated as below:

Minimize $z=\sum _{i=1}^{n}\sum _{j=1}^{n}c_{ij}x_{ij}$

Subject to:

$\sum _{j=1}^{n}x_{ij}-\sum _{k=1}^{n}x_{ki}={\begin{cases}1&{\text{if }}i=s{\text{ (source)}}\\0,&{\text{otherwise}}\\-1&{\text{if }}i=t{\text{ (sink)}}\end{cases}}$

$x_{ij}\geq 0~~\forall (i,j)\in E$

The first term of the constraint is the total outflow of the node i, and the second term is the total inflow. So, the formulation above could be seen as one unit of flow being supplied by the origin, one unit of flow being demanded by the destination, and no net inflow or outflow at any intermediate nodes. These constraints mandate a flow of one unit, amounting to the active path, from the origin to the destination. Under this constraint, the objective function minimizes the overall path distance from the origin to the destination.

Similarly, the integrality of the network problem applies here, precluding the unreasonable fractioning. With supply and demand both being integer (one here), the edges can only have integer amount of flow in the result solved by simplex method. ^[6]

In addition, the point-to-point model above can be further extended to other problems. A number of real life scenarios require visiting multiple places from a single starting point. This “Tree Problem” can be modeled by making small adjustments to the original model. In this case, the source node should supply more units of flow and there will be multiple sink nodes demanding one unit of flow. Overall, the objective and the constraint formulation are similar. ^[4]

Real Life Examples

Network problems have many applications in all kinds of areas such as transportation, city design, resource management and financial planning.^[6]

There are several special cases of network problems, such as the shortest path problem, minimum cost flow problem, assignment problem and transportation problem.^[6] Three application cases will be introduced here.

The minimum cost flow problem

Fig. 8. Illustration of the ship subnetwork.^[10]

Fig. 9. Illustration of cargo subnetwork.^[10]

Minimum cost flow problems are pervasive in real life, such as deciding how to allocate temporal quay crane in container terminals, and how to make optimal train schedules on the same railroad line.^[8]

R. Dewil and his group use MCNFP to assist traffic enforcement.^[9] Police patrol “hot spots”, which are areas where crashes occur frequently on highways. R. Dewil studies a method intended to estimate the optimal route of hot spots. He describes the time it takes to move the detector to a certain position as the cost, and the number of patrol cars from one node to next as the flow, in order to minimize the total cost.^[9]

The assignment problem

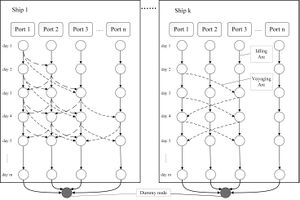
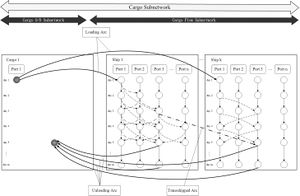
Dung-Ying Lin studies an assignment problem in which he aims to assign freights to ships and arrange transportation paths along the Northern Sea Route in a manner which yields maximum profit.^[10] Within this network  composed of a ship subnetwork and a cargo subnetwork( shown as figure 8 and figure 9), each node corresponds to a port at a specific time and each arc represents the movement of a ship or a cargo. Other types of assignment problems are faculty scheduling, freight assignment, and so on.

The shortest path problem

Shortest path problems are also present in many fields, such as transportation, 5G wireless communication, and implantation of the global dynamic routing scheme.^[11][12][13]

Qiang Tu and his group studies the constrained reliable shortest path (CRSP) problem for electric vehicles in the urban transportation network. ^[14] He describes the reliable travel time of path as the objective item, which is made up of planning travel time of path and the reliability item. The group studies the Chicago sketch network consisting of 933 nodes and 2950 links and the Sioux Falls network consisting of 24 nodes and 76 links. The results show that the travelers’ risk attitudes and properties of electric vehicles in the transportation network can have a great influence on the path choice.^[14] The study can contribute to the invention of the city navigation system.

Numerical Example and Solution

A Food Distributor Company is farming and collecting vegetables from farmers to later distribute to the grocery stores. The distributor has specific agreements with different third-party companies to mediate the delivery to the grocery stores. In a particular month, the company has 600 ton vegetables to deliver to the grocery store. They have agreements with two third-party transport companies A and B, which have different tariffs for delivering goods between themselves, the distributor, and the grocery store. They also have limits on transport capacity for each path. These delivery points are numbered as shown below, with path 1 being the transport from the Food Distributor Company to the transport company A. The limits and tariffs for each path can be found in the Table 2 below, and the possible transportation connections between the distributor company, the third-party transporters, and the grocery store are shown in the figure below. The distributor companies cannot hold any amount of food, and any incoming food should be delivered to an end point. The distributor company wants to minimize the overall transport cost of shipping 600 tons of vegetables to the grocery store by choosing the optimal path provided by the transport companies. How should the distributor company map out their path and the amount of vegetables carried on each path to minimize cost overall?

Table 2. Product Limits and Tariffs for each Path

	1	2	3	4	5	6
Product limit (ton)	250	450	350	200	300	500
Tariff ($/ton)	10	12.5	5	7.5	10	20

This question is adapted from one of the exercise questions in chapter 8 of the book: Applied Mathematical Programming by Bradley, Hax and Magnanti ^[3].

Formulation of the Problem:

The problem can be formulated as below where variables $x_{1},x_{2},x_{3},...,x_{6}$ denote the tons of vegetables carried in paths 1 to 6. The objective function stated in the first line is to minimize the cost of the operation, which is the summation of the tons of vegetables carried on each path multiplied by the corresponding tariff: $\sum _{i=1}^{6}x_{i}t_{i}$.

${\begin{array}{lcl}\min z=10x_{1}+12.5x_{2}+5x_{3}+7.5x_{4}+10x_{5}+20x_{6}\\s.t.\qquad x_{5}=x_{1}-x_{3}+x_{4}\\\ \ \ \quad \qquad x_{6}=x_{2}+x_{3}-x_{4}\\\ \ \ \quad \qquad x_{5}+x_{6}=600\\\ \ \ \quad \qquad x_{1}+x_{2}=600\\\ \ \ \quad \qquad x1\leq 250\\\ \ \ \quad \qquad x_{2}\leq 450\\\ \ \ \quad \qquad x_{3}\leq 350\\\ \ \ \quad \qquad x_{4}\leq 200\\\ \ \ \quad \qquad x_{5}\leq 300\\\ \ \ \quad \qquad x_{6}\leq 500\\\ \ \ \quad \qquad x_{1},x_{2},x_{3},x_{4},x_{5},x_{6}\geq 0\\\end{array}}$

The second step is to write down the constraints. The first constraint ensures that the net amount present in the Transport Company A, which is the deliveries received from path 1 and path 2 minus the transport to Transport Company B should be delivered to the grocery store with path 5. The second constraint ensures this for the Transport Company B. The third and fourth constraints are ensuring that the total amount of vegetables shipping from the Food Distributor Company and the total amount of vegetables delivered to the grocery store are both 600 tons. The constraints 5 to 10 depict the upper limits of the amount of vegetables that can be carried on paths 1 to 6. The final constraint depicts that all variables are non-negative.

Solution of the Problem:

This problem can be solved using Simplex Algorithm [15] or the GAMS optimization platform. The steps of the solution using the GAMS platform is as follows:

The first step is to list the variables, which are the tons of vegetables that will be transported in routes 1 to 6. The paths can be denoted as$x_{1},x_{2},x_{3},...,x_{6}$ . The objective function is the overall cost: z.

variables x1,x2,x3,x4,x5,x6,z;

The second step is to list the equations which are the constraints and the objective function. The objective function is a summation of the amount of vegetables carried in path i, multiplied with the tariff of path i for all i:  $\sum _{i=1}^{6}x_{i}t_{i}$

Overall, there are 10 constraints in this problem. The constraints c1, and c2 are equations for the paths 5 and 6. The amount carried in path 5 can be found by summing the amount of vegetables incoming to Transport Company A from path 1 and path 4, minus the amount of vegetables leaving Transport Company A with path 3. This can be attributed to the restriction that barrs the companies from keeping any vegetables and requires them to eventually deliver all the incoming produce. The equality c1 ensures that this constraint holds for path 5 and c2 for path 6.

Constraint c3 ensures that the sum of vegetables carried in path 1 and path 2 add to the total of 600 tons of vegetables that leave the Food Distributor Company. Likewise, the constraint c4 ensures that the sum amount of food transported in paths 5 and 6 adds up to 600 tons of vegetables that have to be delivered to the grocery store.

Constraints c5 to c10 shows the maximum amount of food that can be transported in each path, as shown in the table.

equations obj,c1,c2,c3,c4,c5,c6,c7,c8,c9,c10;

obj.. z=e= 10*x1+12.5*x2+5*x3+7.5*x4+10*x5+20*x6;

c1.. x5 =e=x1-x3+x4;

c2.. x6=e=x2+x3-x4;

c3.. x5+x6=e=600;

c4.. x1+x2=e=600;

c5.. x1=l=250;

c6.. x2=l=450;

c7.. x3=l=350;

c8.. x4=l=200;

c9.. x5=l=300;

c10.. x6=l=500;

x1.lo=0;

x2.lo=0;

x3.lo=0;

x4.lo=0;

x5.lo=0;

x6.lo=0;

After listing the variables, objective function and the constraints, the final step is to call the solver and define the type of the optimization problem. In this case the problem will be solved with a Linear Programming algorithm to minimize the objective (cost) function.

model problem1 /all/ ;

solve problem1 using lp minimizing z;

The GAMS code yields the results below:

x1 = 250, x2 = 350, x3 = 0, x4 = 50, x5 = 300, x6 = 300, z =16250.

Reference

3. Bradley, S. P., Hax, A. C., & Magnanti, T. L. (1977). Network Models. In Applied mathematical programming (p. 259). Reading, MA: Addison-Wesley.

4. Practical Optimization: A Gentle Introduction, Chapter 10 Network Flow Programming, John W. Chinneck, 2017.

5. Formulation and Analysis of Linear Programs, Chapter 5 Network Flows, Benjamin Van Roy and Kahn Mason, September 26, 2005.

6. Vanderbei, R. J. Network Flow Problem (chapter 14). In R. J. Vanderbei (Ed.), Linear programming: Foundations and extensions. Boston: Springer, 2008.

8. Kuban Altınel, Necati Aras, Zeynep Şuvak, Z. Caner Taşkın, Minimum cost noncrossing flow problem on layered networks, Discrete Applied Mathematics, 2019.

9. R. Dewil, P. Vansteenwegen, D. Cattrysse, D. Van Oudheusden, A minimum cost network flow model for the maximum covering and patrol routing problem, European Journal of Operational Research, 2015.

10. Dung-Ying Lin, Yu-Ting Chang, Ship routing and freight assignment problem for liner shipping: Application to the Northern Sea Route planning problem, Transportation Research Part E: Logistics and Transportation Review, 2018.

11. Qiang Tu, Lin Cheng, Tengfei Yuan, Yang Cheng, Manman Li, The constrained reliable shortest path problem for electric vehicles in the urban transportation network, Journal of Cleaner Production, 2020.

12. Ying Guo, Shenghong Li, Wen Jiang, Bo Zhang, Yinghua Ma, Learning automata-based algorithms for solving the stochastic shortest path routing problems in 5G wireless communication, Physical Communication, 2017.

13. N. Ben Haddou, H. Ez-zahraouy, A. Rachadi, Implantation of the global dynamic routing scheme in scale-free networks under the shortest path.

14. Qiang Tu, Lin Cheng, Tengfei Yuan, Yang Cheng, Manman Li, The constrained reliable shortest path problem for electric vehicles in the urban transportation network, Journal of Cleaner Production, 2020.