Sparse Reconstruction with Compressed Sensing: Difference between revisions
Molokaicat (talk | contribs) |
Molokaicat (talk | contribs) |
||
| Line 375: | Line 375: | ||
The theory was a buildup from what is an inverse problem and sparsity. There it develops into the l0 norm and then concludes l1 norm which are sufficient conditions for basis pursuit. | The theory was a buildup from what is an inverse problem and sparsity. There it develops into the l0 norm and then concludes l1 norm which are sufficient conditions for basis pursuit. | ||
Although the sensing matrix fulfills RIP of order k in some cases, establishing that a given matrix satisfies RIP's conditions is NP-hard in general. In many cases verifying the sensing matrix isn't a reasonable task. So designing the sensing matrix is crucial. It needs to satisfy RIP and be well suited for the problem domain. As well as needs to be computational less of a burden. This takes some creativity and some understanding of the problem domain. | Although the sensing matrix fulfills RIP of order k in some cases, establishing that a given matrix satisfies RIP's conditions is NP-hard in general. In many cases verifying the sensing matrix isn't a reasonable task. So designing the sensing matrix is crucial. It needs to satisfy RIP and be well suited for the problem domain. As well as needs to be computational less of a burden. This takes some creativity and some understanding of the problem domain. It may be concluded the sensing matrix is the most important | ||
component and is deffenetaly the most philosophical. | |||
== Referencse == | == Referencse == | ||
Revision as of 16:53, 20 December 2021
Author: Ngoc Ly (SysEn 5800 Fall 2021)
Introduction
sub module goal
The goal of compressed sensing is to solve the underdetermined linear system in which the number of variables is much greater than the number of observations, resulting in an infinite number of signal coefficient vectors for the same set of compressive measurements . The objective is to reconstruct a vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} in a given of measurements Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} and a sensing matrix A. Instead of taking a large number of high-resolution measurements and discarding the majority of them, consider taking far fewer random measurements and reconstructing the original Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} with high probability from its sparse representation.
sub modual
Begin with a linear equation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = A x + e} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A \in \mathbb{R}^{M \times N}} is a sensing matrix that must be obtained and will result in either exact or approximated optimum solution depending on how it is chosen, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \in \mathbb{R}^{N}} is a signal vector with at most Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} -sparse entries, which means Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} has Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} non-zero entries, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [ N ] = \{ 1, \dots , N \} } be an index set, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y \in \mathbb{R}^{M}} is a compressed measurement vector, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [ M ] = \{ 1, \dots , M \} } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e \in \mathbb{R}^{M}} is a noise vector and assumed to be bounded Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \| e \|_2 \leq \eta} if it exists, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M \ll N} .
sub module sparsity
A vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is said to be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} -sparse in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^N} if it has at most Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} nonzero coefficients. The support of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle supp(x) = \{i \in [N] : x_i \neq 0 \}} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} -sparse signal when the cardinality Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |supp(x)| \leq k} . The set of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} -sparse vectors is denoted by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Sigma_k = \{x \in \mathbb{R}^N : \|x\|_0 \leq k \}} . Consequently, there are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \binom{N}{k}} different subsets of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} -sparse vectors. If a random Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} -sparse Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is drawn uniformly from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Sigma_k} , its entropy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \log \binom{N}{k}} is approximately equivalent to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k \log \frac{N}{k}} bits are required for compression of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Sigma_k} ~cite(Measurements vs Bits).
The idea is to search for the sparsest Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \in \Sigma_k}
from the measurement vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y \in \mathbb{R}^M}
and a sensing matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A \in \mathbb{R}^{M \times N}}
with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M \ll N }
. If the number of linear measurements is at least twice as its sparsity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
, i.e., Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M \geq 2k}
, then there exists at most one signal Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \in \Sigma_k}
that satisfies the constraint Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = A x}
and produce the correct result for any Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \in \Sigma_k}
[coluccia2015 book7]. Hence, the reconstruction problem can be formulated as an Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l_0}
"norm" program.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{x} = \underset{x \in \Sigma_k}{arg min} \|x\|_0 \quad s.t. \quad y = A x}
This optimization problem minimizes the number of nonzero entries of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} subject to the constraint Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = Ax } , that is to find the sparsest element in the affine space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{ x \in \mathbb{R}^N : A x = y\}} [2019 book33]. It turns out to be a combinatorial optimization problem, which is NP-Hard because it includes all possible sets of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} -sparse out of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [N]} . Furthermore, if noise is present, the recovery is unstable [Buraniuk "compressed sensing"].
Restricted Isometry Property (RIP)
A matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} is said to satisfy the RIP of order Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} if for all Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \in \Sigma_k} has a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_k \in [0, 1)} . A restricted isometry constant (RIC) of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} is the smallest Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_k} satisfying this condition [2019 book38, coluccia2015 book7].
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1 - \delta_k) \| x \|_2 ^2 \leq \| A x \|_2^2 \leq (1 + \delta_k) \| x \|_2 ^2}
Under projections through matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} , the restricted isometry property allows Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} -sparse vectors to have unique measurement vectors Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} . If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} meets RIP, then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} does not send two distinct Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} -sparse Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \in \Sigma_k} to the same measurement vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} , indicating that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is a unique solution under RIP.
If the matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A \in \mathcal{R}^{M \times N}}
satisfies the RIP condition of order Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2k}
and the constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_{2k} \in [0,1)}
, there are two distinct Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k}
-sparse vectors in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Sigma_{2k}}
. When they are equal, the restricted isometry property holds. If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A}
is a -order RIP matrix, it means that no two Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k}
-sparse vectors are mapped to the same measurement vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y}
by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A}
. In other words, when working with sparse vectors, the RIP ensures that the columns of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A}
are nearly orthonormal. Furthermore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A}
is an approximately norm-preserving function, which means that it preserves its distance when mapping for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k}
-sparse signals for all or more as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_k}
approaches zero. [Candes, Romberg, Tao[4]] demonstrate that if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k}
-sparse, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A}
satisfies the RIP of order Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2k}
with RIP-constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_{2k} < \sqrt(2) - 1}
, then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l_1}
gives a unique sparse solution. The Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l_1}
convex optimization problem is the same as the solution to the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l_0}
program and can solve by the Linear Program [2019 book38, coluccia2015 book7]. Hence, the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ell_1}
reconstruction problem is as followed which can be solved by basis pursuit.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{x} = \underset{x \in \Sigma_k}{arg min} \|x\|_1 \quad s.t. \quad y = A x}
Theory
Two main things need to be considered when recovering Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
- (1) The design of the sensing matrix
- (2) The recovery algorithm
Sensing Matrix
Although the sensing matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} satisfies RIP of order Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} in some situations, confirming a given matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} meets RIP's criteria is NP-hard in general. As a result, designing an efficient sensing matrix is critical. These sensing matrices are responsible for signal compression at the encoder end and accurate or approximate reconstruction at the decoder end. For signal compression, different sensing matrices are utilized in compressed sensing. There are random, deterministic, structural, and optimized sensing matrices are used in compressed sensing [2020_book].
- Random Sensing Matrices
Some classes of random matrices satisfy RIP, specifically those matrices with independent and identically distributed (i.i.d.) entries drawn from a sub-Gaussian distribution. It requires the number of measurements, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M = O(k log(N/k))} , to recover Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} with high probability. Other popular random sensing matrices are Gaussian, Bernoulli, or Rademacher distributions. However, those random dense matrices incur tremendous computational and memory costs, making them unsuitable for large-scale applications. Several researchers have turned to sparse measurement matrices such as binary or bi-adjacency matrices rather than random matrices to address this issue. Nonetheless, those sparse matrices are unstructured in the same way that acyclic networks or trees are. Fortunately, the new random Weibull matrices [9] are built with appropriate observations and provide exact sparse signal reconstruction with a greater probability [2020_book].
- Deterministic Sensing Matrices
Although deterministic sensing matrices are insufficient to satisfy the RIP condition, they can be used to provide instances for novel concepts. The Vandermond Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k \times N} matrices are one of the best deterministic matrices for recovering the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} -sparse signal; however, the reconstruction technique gets unstable as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} rises. Despite the lack of RIP support in the deterministic sensing matrices, it successfully recovered the original sparse signal for the chirp function-based employing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M \times M^2} complex-valued deterministic matrices. According to the researchers Amini and Marvasti [13], binary, bipolar, and ternary matrices are deterministic constructions of sensing matrices that satisfy the RIP of order Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} . Because of the cyclic feature, the reconstruction process can be sped up using a fast Fourier transform (FFT) technique. Another type of deterministic CS sensing matrix is one based on mutual coherence. The finite geometry-based sparse binary matrices were constructed with low coherence [18,19]. The sparseness property of matrices aids in reducing storage requirements and improving the reconstruction process [2020_book].
- Structural Sensing Matrices
Sensing technologies require structured measurement matrices to perform a variety of tasks. Those matrices can be easily created with a small number of parameters. Furthermore, structured matrices can be used to speed the recovery performance of algorithms, making these matrices suitable for big data challenges. Many researchers created Toeplitz and circulant random sensing matrices used in multipath sparse channel estimation and network systems. In terms of estimated accuracy, signal reconstruction speed, and coherence, these matrices perform similar to i.i.d. Gaussian satisfies RIP with high probability. The new sparse block circulant matrix (SBCM) structure greatly reduces computational complexity. Other structural sensing matrices include the Hadamard matrix, which provides near-optimal assurances of recovery while requiring less complexity and so allowing for simple hardware implementation [2020_book].
- Optimized Sensing Matrices
In order to accomplish high-quality signal reconstruction, the sensing matrices must satisfy RIP. Regardless of what might be expected, the RIP is difficult to verify. Another method for validating the RIP is to compute the mutual coherence between the sensing matrix and the sparse matrix or figure the Gram matrix as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G = A^{T} A \in \mathbb{R}^{N \times N}} . The objective is to improve the sensing matrix to lower coherence using numerous strategies such as the random-detecting framework-based improvement strategy using the shrinkage technique and the irregular estimation of sensing matrix improvement employing a symmetrical strategy. Another technique is to optimize the sensing matrix using a block-sparsified dictionary approach, decreasing the total inter-block and sub-block coherence of the dictionary matrix and thereby significantly increasing the reconstruction [2020_book]
Mutual Coherence
The recovery algorithm often refers to the measurement of quantities that are appropriate to the measurement matrix (sensing matrix), i.e., the coherence. In general, the performance of the recovery algorithm gets better if the coherence is getting smaller. It means the columns of the matrices that have medium size are well-conditioned (governed).
Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A \in R^{M \times N}}
and assume Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ell_2}
-normalized columns of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A}
, the mutual coherence Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu = \mu(A)}
is defined by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu(A) = \underset{1 \leq i \neq j \leq N}{max} {\frac{| \langle a_i, a_j \rangle |}{ \| a_i \|_2 \| a_j \|_2}}} [1] , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_i} is the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} th column of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A}
The feasibility of attaining the lower bounds for the coherence of a matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A \in R^{M \times N}}
, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M < N}
with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ell_2}
-normalized columns, and the columns of the matrix are equiangular tight frames defined as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu(A) \geq \sqrt{\frac{N - M}{M(N-1)}}}
In compressed sensing, a small coherence and a sensing matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M \times N}
, where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N}
is much larger than Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M}
, are the major important requirements.
Let a matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A \in R^{M \times N}} with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ell_2} -normalized columns and let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s \in [N]} . Then for all Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s} -sparse vectors Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \in \mathbb{N}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1 - \mu(s-1)) \| x \|_2 ^2 \leq \| A x \|_2^2 \leq (1 + \mu(s-1)) \| x \|_2 ^2}
Algorithms
Three big groups of algorithms are:[2]
- Optimization methods: includes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ell_1} minimization i.e. Basis Pursuit, and quadratically constraint Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ell_1}
minimization i.e. basis pursuit denoising.
- Greedy methods: include orthogonal matching pursuit (OMP) and compressive sampling matching pursuit (CoSaMP).
- Thresholding-based methods: such as iterative hard thresholding (IHT) and iterative soft thresholding (IST), approximate IHT or AM-IHT, and many more.
More cutting-edge methods include dynamic programming.
We will cover one, i.e. IHT. WHY IHT THEN? Basis pursuit, matching pursuit type algorithms belong to a more general class of iterative thresholding algorithms. [3] So IHT seems like the ideal place to start. If everything compliment with RIP, then IHT has fast convergence.
Algorithm IHT
The Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ell_1} convex program mentioned in introduction has an equivalent nonconstraint optimization program.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \underset{y}{min} \| f{y} - A f{x} \|_2^2 + \lambda \| f{y} \|_0} (cite IT for sparse approximations) ??? Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{f{x}} = arg \underset{s}{min} \frac{1}{n} \| f{y} - A f{x}\|_2^2 + \lambda \| f{x}\|_1} [1]. In statistics we call the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ell_1} regularization LASSO with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} as the regularization parameter. This is the closest convex relaxation to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l_0} the first program mentioned in the introduction.[The Benefit of Group Sparsity]
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_v^{(n)} = \nabla f_v(x^{(n)}) = - A_v^T( f{y} - A f{x})} Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^{n+1} = \mathcal{H}\left( f{x}^{(n)} - \tau \sum_{j \in N}^{N} z_v^{(n)}\right)}
sub modual
Define the threashholding operators as: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_k[x] = \underset{z \in \sum_k}{argmin} \| x - z\|_2} selects the best-k term approximation for some k.
Stopping criterion is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \| y - A x^{(n)}\|_2 \leq \epsilon} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \mbox{iff} \ \mbox{RIC}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_{3k} < \frac{1}{\sqrt{32}}} [4]
- Input Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A, y, e \ \mbox{with} \ y = A x + e} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k}
- output Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IHT(y, A, \mathcal{k}) } , an Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} -sparse solution to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
- Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^{(0)} = 0; n = 0}
- While stopping criterion false do
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^{(n+1)} \leftarrow \mathcal{H}_{k} \left[ x^{(n)} + A^{*} (y - A x^{(n)}) \right]}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n \leftarrow n + 1 }
- end while
- return: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IHT(y, A, k) \leftarrow x^{(n)}}
is an Adjoint matrix i.e. the transpose of it's cofactor.
Numerical Example
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x = \left[ 0.1779, 1.1649, -0.8262 , -1.014 , -0.7975, 0.1883 , 0.2648 , -0.9036 , 0.9409 , 0.4295 \right] }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A = \left[ \begin{matrix} 1.24302 & 0.512088 & 0.727509 & -0.621372 & -0.167216 & 1.28429 & 1.80216 & -0.860403 & -0.190791 & 0.235666\\ -0.199659 & 0.197401 & -0.496226 & 1.1034 & -1.06153 & 0.0130745 & -0.402581 & 0.788863 & 0.591947 & -0.355693\\ 0.0202145 & -0.0043102 & -1.39167 & -0.873447 & 0.253648 & 1.59332 & 0.988392 & -1.32271 & -0.951241 & -0.192874\\ 0.238206 & 1.43934 & -1.08785 & -0.807931 & 0.285027 & -2.64908 & -0.140972 & -0.215606 & -0.760412 & 1.77824 \\ -0.17931 & -1.31525 & -0.0348558 & -0.550808 & 0.460217 & -1.5188 & -1.45967 & 0.508893 & -0.942668 & 1.1059\\ \end{matrix} \right] }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{x} = arg \underset{x \in \Sigma_x}{min} \frac{1}{a} \| y - A x\|_2^2 + \lambda \| x\|_1}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a = 2} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda = 10^{-1}}
sub module iteration 1
calculate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b = x + \frac{1}{a} * A^T (A x - y)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b = [-1.1194851676858286, -0.5425433278394107, 1.1296652382901562, 3.3691735377460557, -1.7975322402864389, 0.812781461654327, -1.5305641112291442, 2.4886377108681788, 2.7744632017898994, -2.450112036057253]}
Thresholding
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^{(1)} = \begin{cases} b^{1} & if \ |b^{(1)}| > \lambda / 2a\\ 0 & if \ |b^{(1)}| \leq \lambda / 2a \end{cases} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x = [-1.1194851676858286, 0.0, 1.1296652382901562, 3.3691735377460557, -1.7975322402864389, 0.812781461654327, -1.5305641112291442, 2.4886377108681788, 2.7744632017898994, -2.450112036057253]}
Calculate the Error Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \|A * x - y \|_2 = 24.020025581623976 }
Calculate the new y
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = A x = [-7.325091157735414, 10.392457780350403, -10.669635806747262, -13.670535847170495, -5.580526608842023]}
Check if error is less then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10 ^{-5} }
sub module iteration 2
calculate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b = x + \frac{1}{a} * A^T (A x - y)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b = [-1.1194851676858286, 0.0, 1.1296652382901562, 3.3691735377460557, -1.7975322402864389, 0.812781461654327, -1.5305641112291442, 2.4886377108681788, 2.7744632017898994, -2.450112036057253]}
Thresholding
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^{(2)} = \begin{cases} b^{2} & if \ |b^{(2)}| > \lambda / 2a\\ 0 & if \ |b^{(2)}| \leq \lambda / 2a \end{cases} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x = [-1.1194851676858286, 0.0, 1.1296652382901562, 3.3691735377460557, -1.7975322402864389, 0.812781461654327, -1.5305641112291442, 2.4886377108681788, 2.7744632017898994, -2.450112036057253]}
Calculate the Error Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \|A * x - y \|_2 = 0.0 }
Calculate the new y
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = A x = [-7.325091157735414, 10.392457780350403, -10.669635806747262, -13.670535847170495, -5.580526608842023]}
Check if error is less then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10 ^{-5} }
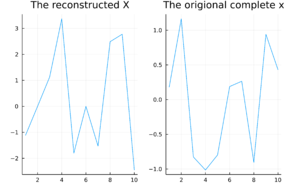
Stopping condition meat
Applications and Motivations
Low-Rank Matrices
The Netflix Prize was accompanied by low-rank matrix recovery or the matrix completion problem. The approach then fills in the missing values in the user's ratings for movies that the user hasn't seen. These estimates are based on ratings from other users, who have similar ratings if a matrix is created with all the users as rows and the movie titles as columns. Because some users' interests will be similar and therefore overlap, it is possible to reduce the degrees of freedom significantly. This low-rank structure is frequently assumed for the problem domain of collaborative filtering ~cited citations.
Dictionary Learning
The goal in dictionary learning is to infer the original dictionary as possible. Instead of using a predefined dictionary, researchers have found that learning the dictionary by obtaining "dynamic features" from training data often yields representation. Biometric features can be taken from video clips of each subject in a dataset and used to populate the dictionary's columns. Using random projections and sparse representations for iris detection for noncontact biometrics-based authentication systems from video samples has been proposed ~cited citations.
Single-pixel cameras
Single-pixel cameras or single detector imaging are used in situations when detectors are either prohibitively expensive or difficult to miniaturize. A microarray is made up of a large number of miniature mirrors that can be individually turned on and off. The mechanism behind the random sampling, which results in low coherence between measurements, is the most important component of the single-pixel camera. This microarray reflects the light from the scene, and a lens combines all of the reflected beams into one sensor, which is the single detector of the camera used to capture the image ~cited citations.
Conclusion
The theory was a buildup from what is an inverse problem and sparsity. There it develops into the l0 norm and then concludes l1 norm which are sufficient conditions for basis pursuit.
Although the sensing matrix fulfills RIP of order k in some cases, establishing that a given matrix satisfies RIP's conditions is NP-hard in general. In many cases verifying the sensing matrix isn't a reasonable task. So designing the sensing matrix is crucial. It needs to satisfy RIP and be well suited for the problem domain. As well as needs to be computational less of a burden. This takes some creativity and some understanding of the problem domain. It may be concluded the sensing matrix is the most important component and is deffenetaly the most philosophical.
Referencse
References
1. Luca Baldassarre, Nirav Bhan, Volkan Cevher, Anastasios Kyrillidis, and Sid-
dhartha Satpathi. Group-sparse model selection: Hardness and relaxations. IEEE
Transactions on Information Theory, 62:6508–6534, 2016.
[11]
Trans. Inf. Theory, 51(12):4203–4215, 2005.
3. Bubacarr Bah, Jannis Kurtz, and Oliver Schaudt. Discrete optimization methods
for group model selection in compressed sensing. April 2019.
4. Chinmay Hegde, Piotr Indyk, and Ludwig Schmidt. Approximation algorithms
for model-based compressive sensing. IEEE Transactions on Information Theory,
61:5129–5147, 2015.
5. Stephen A. Vavasis. Elementary proof of the spherical section property for random
matrices. Univer-sity of Waterloo, Waterloo,Technical report, 2009.
[12]
[13]
Cite error: Closing </ref> missing for <ref> tag
13. D.L. Donoho and Y. Tsaig. Recent advances in sparsity-driven signal recovery.
volume 5, pages v/713–v/716 Vol. 5, Philadelphia, PA, USA, 2005. IEEE.
14. Junzhou Huang, Tong Zhang, and Dimitris Metaxas. Learning with structured
sparsity. Journal of Machine Learning Research (JMLR), 12:3371–3412, 2011.
15. Binbin Lu, Huabo Sun, Paul Harris, Miaozhong Xu, and Martin Charlton.
Shp2graph: Tools to convert a spatial network into an igraph graph in r. 7:293.
[14]
[15]
[16]
1019. Qingbao Yu, Jiayu Chen, Yuhui Du, Jing Sui, Eswar Damaraju, Jessica A. Turner,
Theo G.M. van Erp, Fabio Macciardi, Aysenil Belger, Judith M. Ford, Sarah
McEwen, Daniel H. Mathalon, Bryon A. Mueller, Adrian Preda, Jatin Vaidya,
Godfrey D. Pearlson, and Vince D. Calhoun. A method for building a genome-
connectome bipartite graph model. Journal of Neuroscience Methods, 320:64–71, may
2019.
20. El kadi Hellel, Samir Hamaci, and Rezki Ziani. Modelling and reliability analysis
of multi-source renewable energy systems using deterministic and stochastic petri
net. The Open Automation and Control Systems Journal, 10(1):25–40, nov 2018.
21. Mark F. Flanagan, Vitaly Skachek, Eimear Byrne, and Marcus Greferath. Linear-
programming decoding of nonbinary linear codes.
IEEE Trans. Inf. Theory,
55(9):4134–4154, 2009.
22. Dieyan Liang and Hong Shen. Efficient algorithms for max-weighted point sweep
coverage on lines. Sensors (Basel, Switzerland), 21, February 2021.
[17]
24. Thomas Blumensath. Accelerated iterative hard thresholding. 92:752–756, 2012.
25. Blumensath Thomas. Eaccelerated eiterative ehard ethresholding.
26. N. Burak Karahanoglu, Hakan Erdogan, and S. Ilker Birbil. A mixed integer linear
programming formulation for the sparse recovery problem in compressed sensing,
2013.
1127. Chinmay Hegde, Piotr Indyk, and Ludwig Schmidt. A nearly-linear time frame-
work for graph-structured sparsity. In International Conference on Machine Learning,
pages 928–937. PMLR, 2015.
28. M. Sandbichler, F. Krahmer, T. Berer, P. Burgholzer, and M. Haltmeier. A novel
compressed sensing scheme for photoacoustic tomography. 75:2475–2494, 2015.
29. B. S. Kashin and V. N. Temlyakov. A remark on compressed sensing. 82:748–755,
2007.
[18]
31. Yonina C. Eldar, Patrick Kuppinger, and Helmut Bolcskei. Block-sparse signals:
Uncertainty relations and efficient recovery. 58:3042–3054, 2010.
32. Wandi Liang, Zixiong Wang, Guangyu Lu, and Yang Jiang. A compressed sensing
recovery algorithm based on support set selection. Electronics, 10(13):1544, 2021.
[19]
34. M Amin Khajehnejad, Weiyu Xu, A Salman Avestimehr, and Babak Hassibi.
Weighted l 1 minimization for sparse recovery with prior information. In 2009 IEEE
international symposium on information theory, pages 483–487. IEEE, 2009.
35. Junzhou Huang, Tong Zhang, and Dimitris Metaxas. Learning with structured
sparsity. March 2009.
36. Kezhi Li and Shuang Cong. State of the art and prospects of structured sensing
matrices in compressed sensing. 9:665–677, 2015.
1237. Ruitao Xie and Xiaohua Jia. Minimum transmission data gathering trees for com-
pressive sensing in wireless sensor networks, 2011.
38. Prateek Jain, Ambuj Tewari, and Purushottam Kar. On iterative hard thresholding
methods for high-dimensional m-estimation. arXiv preprint arXiv:1410.5137, 2014.
39. Yanglong Lu and Yan Wang. Physics-based compressive sensing approach to mon-
itor turbulent flow. 58:3299–3307, 2020.
[20]
41. Junzhou Huang and Tong Zhang. The benefit of group sparsity. 38, 2010.
42. Piotr Indyk and Ilya Razenshteyn. On model-based rip-1 matrices. In International
Colloquium on Automata, Languages, and Programming, pages 564–575. Springer,
2013.
43. Bubacarr Bah, Luca Baldassarre, and Volkan Cevher. Model-based sketching and
recovery with expanders, 2014.
44. A. M. Geoffrion. Generalized benders decomposition. 10:237–260, 1972.
45. J. F. Benders. Partitioning procedures for solving mixed-variables programming
problems. 2:3–19, 2005.
46. T. L. Magnanti and R. T. Wong. Accelerating benders decomposition: Algorithmic
enhancement and model selection criteria. 29:464–484, 1981.
47. Richard G. Baraniuk, Volkan Cevher, Marco F. Duarte, and Chinmay Hegde.
Model-based compressive sensing. arXiv e-prints, page arXiv:0808.3572, August
2008.
[21]
[22]
[23]
- ↑ 1.0 1.1 Cite error: Invalid
<ref>tag; no text was provided for refs named:1 - ↑ Cite error: Invalid
<ref>tag; no text was provided for refs named:0 - ↑ Cite error: Invalid
<ref>tag; no text was provided for refs named:4 - ↑ Cite error: Invalid
<ref>tag; no text was provided for refs named:2 - ↑ D. L. Donoho, “Compressed sensing,” vol. 52, pp. 1289–1306, 2006, doi: 10.1109/tit.2006.871582.
- ↑ E. J. Candès and T. Tao, “Decoding by linear programming,” IEEE Trans. Inf. Theory, vol. 51, no. 12, Art. no. 12, 2005, doi: 10.1109/TIT.2005.858979.
- ↑ D. L. Donoho, “Compressed sensing,” vol. 52, pp. 1289–1306, 2006, doi: 10.1109/tit.2006.871582.
- ↑ T. Blumensath and M. E. Davies, “Iterative Hard Thresholding for Compressed Sensing,” May 2008.
- ↑ S. Foucart and H. Rauhut, A mathematical introduction to compressive sensing. New York [u.a.]: Birkhäuser, 2013.
- ↑ R. G. Baraniuk, “Compressive Sensing [Lecture Notes],” IEEE Signal Processing Magazine, vol. 24, no. 4, Art. no. 4, 2007, doi: 10.1109/MSP.2007.4286571.
- ↑ 2. Emmanuel J. Candès and Terence Tao. Decoding by linear programming. IEEE
- ↑ 6. Angshul Majumdar. Compressed sensing for engineers. Devices, circuits, and systems. CRC Press, Taylor & Francis Group, Boca Raton, FL, 2019. Includes bibliographical references and index.
- ↑ 7. Simon Foucart and Holger Rauhut. A mathematical introduction to compressive sens- ing. Applied and numerical harmonic analysis. Birkhäuser, New York [u.a.], 2013.
- ↑ 16. Giulio Coluccia, Chiara Ravazzi, and Enrico Magli. Compressed sensing for dis- tributed systems, 2015.
- ↑ 17. Mohammed Rostami. Compressed sensing with side information on feasible re- gion, 2013.
- ↑ 18. Thomas Blumensath and Mike E. Davies. Iterative hard thresholding for com- pressed sensing. May 2008.
- ↑ 23. Laska Jason Noah. Rice university regime change: Sampling rate vs. bit-depth in compressive sensing, 2011.
- ↑ 30. Richard Baraniuk, Mark Davenport, Ronald DeVore, and Michael Wakin. A simple proof of the restricted isometry property for random matrices. 28:253–263, 2008.
- ↑ 33. Richard G. Baraniuk. Compressive sensing [lecture notes]. IEEE Signal Processing Magazine, 24(4):118–121, 2007.
- ↑ 40. Emmanuel Candes, Justin Romberg, and Terence Tao. Stable signal recovery from incomplete and inaccurate measurements. March 2005.
- ↑ 1348. Niklas Koep, Arash Behboodi, and Rudolf Mathar. An introduction to compressed sensing, 2019.
- ↑ 49. Martin Burger, Janic Föcke, Lukas Nickel, Peter Jung, and Sven Augustin. Recon- struction methods in thz single-pixel imaging, 2019.
- ↑ 50. J. K. Pillai, V. M. Patel, R. Chellappa, and N. K. Ratha. Secure and robust iris recognition using random projections and sparse representations. 33:1877–1893, 2011.



