Duality

Author: Claire Gauthier, Trent Melsheimer, Alexa Piper, Nicholas Chung, Michael Kulbacki (SysEn 6800 Fall 2020)

Steward: TA's name, Fengqi You

Introduction

Every linear programming optimization problem may be viewed either from the primal or the dual, this is the principal of duality. Duality develops the relationships between one linear programming problem and another related linear programming problem. For example in economics, if the primal optimization problem deals with production and consumption levels, then the dual of that problem relates to the prices of goods and services. The dual variables in this example can be referred to as shadow prices.

The shadow price of a constraint ...

Theory, methodology, and/or algorithmic discussions

Definition:

Primal

Maximize Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=\textstyle \sum_{j=1}^n \displaystyle c_j x_j}

subject to:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \textstyle \sum_{j=1}^n \displaystyle a_{i,j} x_j\lneq b_j \qquad (i=1, 2, ... ,m) }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_j\gneq 0 \qquad (j=1, 2, ... ,n) }

Dual

Minimize Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v=\textstyle \sum_{i=1}^m \displaystyle b_i y_i}

subject to:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \textstyle \sum_{i=1}^m \displaystyle a_{i,j} y_i\gneq c_j \qquad (j=1, 2, ... , n) }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_i\gneq 0 \qquad (i=1, 2, ... , m)}

Between the primal and the dual, the variables Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} switch places with each other. The coefficient (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_j} ) of the primal becomes the Right Hand Side (RHS) of the dual. The RHS of the primal (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_j} ) becomes the coefficient of the dual. The less than or equal to constraints in the primal become greater than or equal to in the dual problem.

Constructing a Dual:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix} \max(c^Tx) \\ \ s.t. Ax\leq b \\ x \geq 0 \end{matrix}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \quad \longrightarrow \quad} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix} \\ \min(b^Ty) \\ \ s.t. A^Tx\geq c \\ y \geq 0 \end{matrix}}

Duality Properties:

Weak Duality

• let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=[x_1, ... , x_n] } be any feasible solution to the primal
• let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = [y_1, ... , y_m] } be any feasible solution to the dual
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \therefore } (z value for x) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \leq } (v value for y)

The weak duality theorem says that the z value for x in the primal is always less than or equal to the v value of y in the dual.

Strong Duality Lemma

• let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=[x_1, ... , x_n] } be any feasible solution to the primal
• let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = [y_1, ... , y_m] } be any feasible solution to the dual
• if (z value for x) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = } (v value for y), then x is optimal for the primal and y is optimal for the dual

Graphical Explanation

Essentially, as you choose values of x or y that come closer to the optimal solution, the value of z for the primal, and v for the dual will converge towards the optimal solution. On a number line, the value of z which is being maximized will approach from the left side of the optimum value while the value of v which is being minimized will approach from the right hand side.

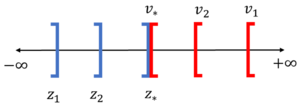
• if the primal is unbounded, then the dual is infeasible
• if the dual is unbounded, then the primal is infeasible

Numerical Example

Construct the Dual for the following maximization problem:

maximize Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=6x_1+14x_2+13x_3}

subject to:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{2}x_1+2x_2+x_3\leq 24}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1+2x_2+4x_3\leq 60}

For the problem above, form augmented matrix A. The first two rows represent constraints one and two respectively. The last row represents the objective function.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A =\begin{bmatrix} \tfrac{1}{2} & 2 & 1 & 24 \\ 1 & 2 & 4 & 60 \\ 6 & 14 & 13 & 1 \end{bmatrix}}

Find the transpose of matrix A

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^T=\begin{bmatrix} \tfrac{1}{2} & 1 & 6 \\ 2 & 2 & 14 \\ 1 & 4 & 13 \\ 24 & 60 & 1\end{bmatrix}}

From the last row of the transpose of matrix A, we can derive the objective function of the dual. Each of the preceding rows represents a constraint. Note that the original maximization problem had three variables and two constraints. The dual problem has two variables and three constraints.

minimize Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=24y-1+60y_2 }

subject to:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{1}{2}y_1+y_2 \geq 6}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2y_1+2y_2\geq 14}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_1+4y_2\geq 13}

References

1. https://ocw.mit.edu/courses/sloan-school-of-management/15-084j-nonlinear-programming-spring-2004/lecture-notes/lec18_duality_thy.pdf
2. http://web.mit.edu/15.053/www/AMP-Chapter-04.pdf