Signomial problems

Author: Megan Paonessa (map465) (SYSEN 5800 Fall 2024)

Stewards: Nathan Preuss, Wei-Han Chen, Tianqi Xiao, Guoqing Hu

Introduction

Signomial problems are a significant advancement in optimization theory, providing a framework for addressing non-convex functions. Unlike convex optimization, where the global minimum can be found efficiently, signomial problems involve objective functions and constraints with complex, non-convex structures[1][2].

Signomial problems involve optimizing a function that is a sum of weighted exponential terms with real exponents, typically expressed as:

$f(x)=\sum _{i=1}^{m}c_{i}\prod _{j=1}^{n}x_{j}^{a_{i,j}}$,

Where:

• $x=[x_{1},x_{2},...,x_{n}]$ are the decision variables.
• $c_{i}\in R$ are coefficients (which can be negative, unlike posynomials.
• $a_{i,j}\in R$ are real exponents.
• $x_{j}>0$ ensures positivity of the variables.

The general form of a signomial problem is:

Minimize: $f(x)=\sum _{i=1}^{m}c_{i}\prod _{j=1}^{n}x_{j}^{a_{i,j}}$,

Subject to: $g_{k}(x)=\sum _{i=1}^{p}d_{i}\prod _{j=1}^{n}x_{j}^{b_{i,j}}\leq 0,$ $k=1,...,K,$

$h_{l}(x)=\sum _{i=1}^{q}e_{i}\prod _{j=1}^{n}x_{j}^{c_{i,j}}=0,$, $l=1,...,L,$

$x_{j}>0,$ $j=1,...,n.$

This formulation[1][2][3] allows for negative coefficients (), which differentiates it from posynomials in geometric programming that restrict coefficients to be positive. This flexibility makes signomial problems applicable to a wider range of non-convex optimization scenarios.

The concept evolved from geometric programming, first introduced in the 1960s, as a method to address optimization problems involving non-linear, real-world phenomena such as energy system design and financial risk management. As outlined by Vanderbei[1] and Boyd[2], these advancements were pivotal in extending linear programming principles to handle non-linear dependencies effectively.

The motivation for studying signomial problems lies in their ability to model critical applications, such as minimizing energy costs in hybrid grids or designing supply chains with economies of scale. Recent research, including work by Nocedal and Wright[3], highlights their growing importance in modern optimization techniques.

--> orig

Sigmoid problems are a class of optimization problems with the objective of maximizing the sum of multiple sigmoid functions. They are defined by their limits at negative and positive infinity. Similar to the unit step function the function approaches 1 as it approaches infinity and approaches -1 as it approaches negative infinity. Sigmoid functions are shaped like an “S”, having both a convex and concave portion. The concave attributes will make solving the problems require a non-linear optimization, increasing computational burden. Though sigmoid problems are harder to solve than ordinary convex programs, they have many useful real-world applications which have encouraged their development. Sigmoid problems have become especially useful in the creation of artificial neural networks that simulate learning. The functionality of sigmoid problems allow in statistical models and other artificial learning.

The S-shape of the individual sigmoid functions made them good representatives of economies of scale, or other situations where the supplier is facing a declining demand function and increased investment leads to a lower average cost to produce each good. Within the sigmoidal problem, the sigmoidal functions within the objective represent that initial increases in investment will increase profitability when there is excess demand at the current price. The inflection point in the sigmoidal functions represents the point where the marginal profit for producing another good becomes 0. At this point the decrease in marginal cost from investing in more production is matched by an equal decrease in willingness to pay by the marginal consumer. Past this point the function determines that increased investment will not increase profitability. These properties of the sigmoid functions allow them to be ideal representatives of situations where initial investment is profitable though a threshold is reached where no additional inputs will be profitable. Other situations that exhibit these characteristics and can be modeled with sigmoidal problems include election planning, lottery prize design, and bidding at an auction. Election planners always desire to find the locations where spending on advertising will have the greatest effect on election results. When designing a lotter, the company wants to design a prize value that encourages many people to buy tickets while still being net profitable for the lottery. At an auction, a bidder may not have enough capital to buy every item they may desire so it is important early on to not waste a disproportionate amount of money winning an item that is not important. A sigmoidal problem maximizing utility can help determine the threshold value to bid on each item.

Algorithm Discussion

Successive Convex Approximation (SCA)

SCA is a practical approach to solving non-convex problems by approximating them as a sequence of convex subproblems. At each iteration, the non-convex terms are linearized around the current solution, and a convex optimization problem is solved[3]. This iterative refinement ensures convergence under specific regularity conditions.

Pseudocode for SCA:

1. Initialize $x^{(0)}$ within the feasible region.
2. Repeat until convergence:
   1. Linearize non-convex terms around $x^{(k)}$.
   2. Solve the resulting convex subproblem.
   3. Update $x^{(k+1)}$.
3. Return $x^{(k+1)}$ as the solution.

Applications of SCA, as demonstrated by Biegler[6], have been successfully implemented in chemical process optimization, where complex reaction networks necessitate iterative refinement of solutions.

Global Optimization Techniques

Global optimization methods such as branch-and-bound and cutting-plane techniques are indispensable for solving signomial problems to global optimality. As described by Ben-Tal[4] and Nemirovski[15], these methods systematically explore the solution space by dividing it into smaller regions and pruning infeasible areas based on objective function bounds.

While these methods guarantee global solutions, their computational intensity makes them suitable for problems of moderate size. Recent advancements in computational power and parallel processing have improved their applicability in larger-scale systems.

Metaheuristics

Heuristic algorithms, including Genetic Algorithms (GA) and Particle Swarm Optimization (PSO), are widely used to tackle large-scale, non-convex signomial problems. These methods, highlighted by Hastie et al.[7], employ probabilistic techniques to explore the solution space efficiently.

For example, GA employs selection, crossover, and mutation operations to iteratively refine solutions, making it suitable for problems in finance and engineering. PSO, inspired by swarm intelligence, has shown promise in optimizing energy systems with non-linear constraints.

Numerical Examples

Chemical Process Optimization Example

The objective is to minimize cost in a chemical production process.

Problem Formulation:

Minimize: $f(x,y)=5x^{-0.5}+10y^{1.2}$

Subject to: ${\begin{cases}x+y\geq 50,\\x>0,\\y>0\end{cases}}$

Using Successive Convex Approximation (SCA), the optimal values are:

$x^{*}=30,$ $y^{*}=20$

This minimizes the cost to:

$f(x^{*},y^{*})=85$

Renewable Energy Portfolio

The objective is to optimize energy costs while meeting production targets.

Problem Formulation:

Minimize: $f(x,y)=100x^{-0.5}+200y^{1.2}$

Subject to: ${\begin{cases}x+y\geq 100,\\x>0,\\y>0\end{cases}}$

Using Successive Convex Approximation (SCA), the optimal values are:

$x^{*}=60,$ $y^{*}=40$

This minimizes the cost to:

$f(x^{*},y^{*})=1500$

Applications

Signomial problems have extensive applications across various domains, including engineering, finance, and energy systems, where complex, non-linear dependencies are common: Engineering:

• Signomial models are integral to optimizing production systems with constraints like material flow, energy efficiency, and system performance.
• Example: In chemical engineering, Biegler et al. [12] demonstrated the use of signomial optimization for designing reactors and separations processes, where reaction kinetics and thermodynamic properties create non-linear constraints.

Energy Systems:

• Balancing renewable and non-renewable energy sources requires modeling complex cost structures and efficiency trade-offs.
• Example: Boyd et al. [14] studied renewable energy grid optimization, where diminishing returns on additional energy investments were captured using signomial formulations.

Finance:

• Signomial optimization is used to model risk-return trade-offs in portfolio management, capturing non-linear relationships between diversification and risk reduction.
• Example: Hastie et al. [7] employed signomial models to manage investment portfolios, balancing risk and expected returns while accounting for market uncertainties.

Conclusion

Signomial problems represent a critical evolution in optimization theory, addressing real-world challenges with non-linear dependencies. Advancements in numerical methods and computational tools continue to expand their applicability, while research into hybrid models and machine learning integration offers promising directions for the future[7][8].

References

1. Vanderbei, R.J., Linear Programming: Foundations and Extensions. Springer, 2008. 2. Boyd, S., Vandenberghe, L., Convex Optimization. Cambridge University Press, 2009.

3. Nocedal, J., Wright, S.J., Numerical Optimization. Springer, 1999.

4. Ben-Tal, A., Robust Optimization. Princeton University Press, 2009.

5. Grossmann, I.E., Advanced Nonlinear Programming. SIAM, 2015.

6. Biegler, L.T., Nonlinear Programming. SIAM, 2010.

7. Hastie, T., Tibshirani, R., The Elements of Statistical Learning. Springer, 2009.

8. Murphy, K., Machine Learning: A Probabilistic Perspective. MIT Press, 2012.

9. Edgar, T.F., Himmelblau, D.M., Optimization of Chemical Processes. McGraw-Hill, 2001.

10. Birge, J.R., Louveaux, F., Introduction to Stochastic Programming. Springer, 2011.

11. Wolsey, L.A., Integer Programming. Wiley, 1998.

12. Biegler, L.T., Systematic Methods of Chemical Process Design. Prentice Hall Press, 1997.

13. Boyd, S., Applications of Convex Optimization in Engineering. Cambridge University Press, 2010.

14. Nemirovski, A., Robust Optimization Techniques in Nonlinear Programming. Springer, 2010.

Sigmoidal Functions

Figure 1: Logistic Sigmoid Function

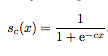
Generally, a sigmoid function is any function having an “S” shape. One portion of the function will be convex while the other portion will be concave. The most common example of the sigmoid function is the logistic function shown in figure 1. However, the definition of sigmoidal functions is very broad: Any function that has real values, one inflection point and has a bell shaped first derivative function. With this definition, all logistic functions, the error function, the cumulative distribution function and many more can be considered sigmoidal functions and may be included in the objective function of a sigmoidal problem. In figure 1, the coefficient 1/c is the temperature constant. As the value of c increases in the sigmoid function, the sigmoid function will approach the shape of a step function.

Sigmoidal Problems

Figure 2: "S" Shape Curve

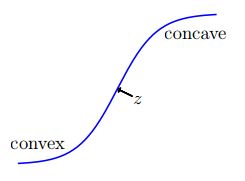
In practice, sigmoid problems consist of an optimization where the objective function is the sum of a set of sigmoid functions. Each of the sigmoid functions only has one input variable that determines the output value. Unless a certain threshold of input value has been exceeded, usually the value of the sigmoid function will be very close to zero. As a result, the solution of a sigmoid problem will consist of all the function input values either being 0 or a number exceeding the sigmoid function threshold. This threshold is depicted as being near z in figure 2. When optimizing inputs to achieve a desired output, usually there is a scarcity of inputs that must be allocated optimally; otherwise there would be no cause for a problem. Thus, the solution of the optimization will exceed the threshold z in as many indexes as possible. Any indexes that were not able to reach z input usually would have an input of 0. This is because, below z total inputs, two functions each with one unit of input will always have a lower combined utility than one sigmoid function with two units of input.

Applications of Sigmoidal Problems

These characteristics of sigmoidal problems make them very useful for certain types of optimizations. In presidential election planning, it is always important to spend campaign advertising dollars in a way which will have the largest impact on electoral count. Since the format of our election is winner-take-all in each state, the states that have the tightest poll results would be the states where the smallest change in poll numbers would most greatly change the overall electoral count. If a campaign team were trying to optimize their advertising spending they would want to create an objective that illustrated how their advertising would have an effect on each state. The campaign would only want to spend money on states that have a feasible change of voting in favor of their candidate. Money spend on states eventually lost is completely wasted. Sigmoidal functions will behave in the same way, only recommending to spend money in a state if they can pass the threshold of getting a majority of voters. They will predict that it is better to spend a lot of money on one state they have a good chance to influence than spend half each on two states where they may end up losing both.

The same logic follows for why sigmoidal problems are useful for optimizing bidding within an auction. Utility is only gained when a desired item is won, so it is always important to set up a function that only calculates utility when the necessary bidding threshold has been passed. There is no use or utility gained from bidding half the value on every item, and sigmoidal functions would appropriately capture this fact.

Sigmoid functions can be very useful in situations where utility gained is not continuous based on proportion but is more of a binary either/or result. They are not as extreme of a binary result as a step function, and the fact that they are fully differentiable makes them much more easily solved. However, since they have concave portions, their solution is not as simple as a linear program and may require software or approximations.

Large arrays of sigmoid problems have also been combined to simulate an artificial neural networks. These neural networks are sets of sigmoid functions used to approximate interconnected neurons, which are very powerful in statistical modeling. The neural networks are created by the aggregation of sigmoidal functions using the back-propagation algorithm. The most common applications of the sigmoidal problems is the density problem. The density of a linear space with uniform convergence can be calculated for a compact set using Cybenko's approximation theorem.

Solving Sigmoidal Problems

Figure 3: Concave Envelope

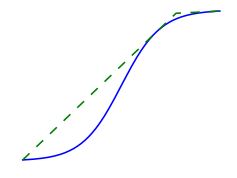
As one of the properties of a sigmoid function is concave portions, simple simplex optimization will not suffice. As computation power has increased in recent decades, solutions of sigmoidal problems has become much more feasible using software available online. Though, solutions with the appropriate software are fairly straightforward and simple, these sorts of problems can be highly difficult to solve by hand. They can rarely be solved at all in the original format and frequently need several creative approximations to leave a problem that is computable by hand. One method that allows simpler by-hand computation is the creation of a convex envelope. Depicted in figure 3, the concave envelope is an approximation of the sigmoidal function that adds a linear portion where the function had been previously convex. This addition, greatly simplifies the function’s computational difficulty. However, it must be noticed, that this approximation will only give an upper bound on the solution as it is including area that it not part of the original constraints. Even with function simplification and approximation, usually there is a large set of functions to be optimized. Depending on the level of approximation, the solution found may not even contain a relevant level of accuracy. In general, software will be the method of choice when dealing with sigmoidal problems.

References

1. J. Birge, F. Louveaux, Introduction to Stochastic Programming, Springer, 2011.

2. Udell, Madeline, and Stephen Boyd. "Maximizing a Sum of Sigmoids." Stanford University, May 2015. Web. May 2015. <http%3A%2F%2Fweb.stanford.edu%2F~udell%2Fdoc%2Fmax_sum_sigmoids>.

3. Srivastava, Vaibhav, and Francesco Bullo. "Knapsack Problems with Sigmoid Utilities." Princeton, July 2013. Web. May 2015. <http%3A%2F%2Fwww.princeton.edu%2F~vaibhavs%2Fpapers%2F2012d-sb>.

4. Rojas, R. "Backpropagation." SpringerReference (2011): n. pag. UBerlin. UBerlin. Web.