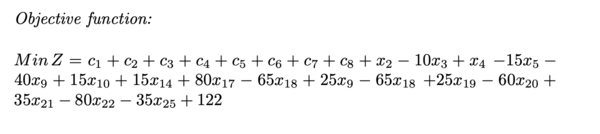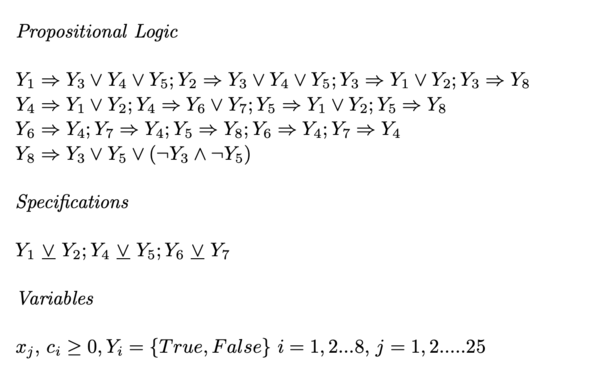Convex generalized disjunctive programming (GDP)
Edited By: Nicholas Schafhauser, Blerand Qeriqi, Ryan Cuppernull
Introduction
[ Insert picture from google doc of GDP branching to Logic Based Methods and Reformulation MI(N)LP ]
Theory
Methodology
The two most common ways of reformulating a GDP problem into an MINLP are through Big-M (BM) and Hull Reformulation (HR). BM is the simpler of the two, while HR results in tighter relaxation (smaller feasible region) and faster solution times. (https://kilthub.cmu.edu/articles/A_hierarchy_of_relaxations_for_nonlinear_convex_generalized_disjunctive_programming/6466535)
Below is an example of the reformulation of the GDP problem from the Theory section reformulated into an MINLP by using the Big-M method.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \min z=f(x)\\ s.t.g(x) \leq 0\\ r_{ki}(x) \leq M^{ki}(1-y_{ki})\quad k \in K,i \in D_k\\ \sum_{i \in D_k} y_{ki} = 1\quad k \in K\\ Hy \geq h\\ x^{lo} \leq x \leq x^{up}\\ x \in \Re^n\\ y_{ki} \in {0,1} \quad k \in K, i \in D_k \end{align}}
Notice that the boolean term from the original GDP has been converted into a numerical {0,1}. The logic relations have also been converted into linear integer constraints (Hy).
(https://kilthub.cmu.edu/articles/journal_contribution/Improved_Big-M_Reformulation_for_Generalized_Disjunctive_Programs/6467063)
This MINLP reformulation can now be used in well-known solvers (list them here) to calculate a solution.
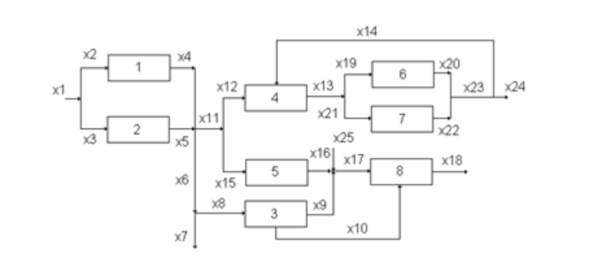
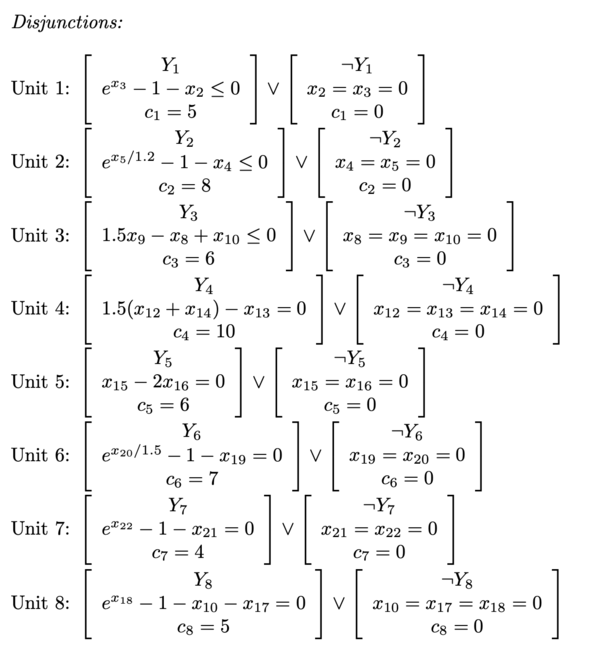
Numerical Example
The following example was taken from: http://egon.cheme.cmu.edu/Papers/IMAGrossmannRuiz.pdf