Stochastic programming
Authors: Roohi Menon, Hangyu Zhou, Gerald Ogbonna, Vikram Raghavan (SYSEN 6800 Fall 2021)
Introduction
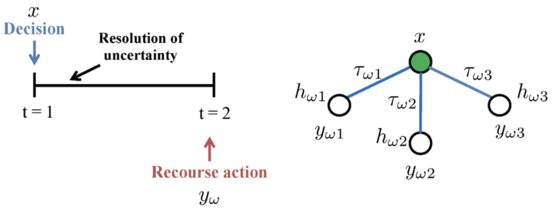
Stochastic Programming, also referred to as Stochastic Optimization, is a mathematical framework to help decision-making processes under uncertainty. [2] With uncertainties being widespread, Stochastic Programming is a risk-neutral mathematical framework that finds application in areas, such as process systems engineering. [3] In process engineering, uncertainties are related to prices, purity of raw materials, customer demands, and yields of pilot reactors, among others. Batch processing has widely been adopted across process industries, and for the stated manufacturing process production scheduling is one of the most crucial decisions to be taken. In a deterministic optimization model, parameters, such as the process of raw materials, availability of raw materials, price of different products, operation time and cost, and order demands are considered without factoring in uncertainty. However, such assumptions are not realistic because uncertainty doesn’t come with forewarning. Hence, uncertainty needs to be factored in always. [4]
In conventional robust optimization, the assumption is made that all decision variables are realized before the realization of uncertainty. Such an approach makes the conventional robust optimization problem overly conservative. [4] Moreover, in manufacturing, not all decisions need to be made “in-the-present,” a stagnated approach to decision making [two-stage approach] can also be adopted. Going beyond, the Stochastic Programming framework can also be applied to a variety of problems across sectors, such as electricity generation, financial planning, supply chain management, mitigation of climate change, and pollution control. [3] The field has evolved from deterministic linear programming by introducing random variables. [5]
Theory, methodology, and/or algorithmic discussion
Two-Stage Stochastic Linear Program with Fixed Recourse:
Modeling through stochastic programming is often adopted because of its proactive-reactive decision-making feature to address uncertainty. [2] Two-stage stochastic programming (TSP) is helpful when a problem requires the analysis of policy scenarios, however, the associated system information is inherently characterized with uncertainty. [3] In a typical TSP, decision variables of an optimization problem under uncertainty are categorized into two periods. Decisions regarding the first-stage variables need to be made before the realization of the uncertain parameters. The first-stage decision variables are proactive for they hedge against uncertainty and ensure that the solution performs well under all uncertainty realizations. [2] Once the uncertain events have unfolded/realized, it is possible to further design improvements or make operational adjustments through the values of the second-stage variables, also known as recourse, at a given cost. The second-stage variables are reactive in their response to the observed realization of uncertainty. [2] Thus, optimal decisions should be made on data that is available at the time the decision is being made. In such a setup, future observations are not taken into consideration. [6] Two-stage stochastic programming is suited for problems with a hierarchical structure, such as integrated process design, and planning and scheduling. [2]
Methodology
The classical two-stage stochastic linear program with fixed recourse [7] is given below:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \min z=c^Tx + E_{\xi}[\min q(\omega)^Ty(\omega)] }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s.t. \quad Ax = b }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \qquad \quad T(\omega)x + Wy(\omega) = h(\omega) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \qquad \quad x \ge 0, y(\omega) \ge 0 }
Where is a known vector in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^{n_1}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} is a known vector in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^{m_1}} . Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W} are known matrices of size Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_1 \times n_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_2 \times n_2} respectively. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W} is known as the recourse matrix.
The first-stage decisions are represented by the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_1 \times 1} vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} . Corresponding to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} are the first-stage vectors and matrices Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} . In the second stage, a number of random events Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega \in \Omega} may realize. For a given realization Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} , the second-stage problem data Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q(\omega)} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h(\omega)} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T(\omega)} become known. [8]
Algorithm discussion
To solve problems related to Two-Stage Linear Stochastic Programming more effectively, algorithms such as Benders decomposition or the Lagrangean decomposition can be used. Benders decomposition was presented by J.F Benders, and is a decomposition method used widely to solve mixed-integer problems. The algorithm is based on the principle of decomposing the main problem into sub-problems. The master problem is defined with only the first-stage decision variables. Once the first-stage decisions are fixed at an optimal solution of the master problem, thereafter, the subproblems are solved and valid inequalities of x are derived and added to the master problem. On solving the master problem again, the algorithm iterates until the upper and lower bound converge. [3] The Benders master problem is defined as being linear or mixed-integer and having fewer technical constraints, while the sub-problems could be linear or nonlinear in nature. The subproblems’ primary aim is to validate the feasibility of the master problem’s solution. [7] Benders decomposition is also known as L-shaped decomposition because once the first stage variables, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} , are fixed then the rest of the problem has a structure of a block-diagonal. This structure can be decomposed by scenario and solved independently. [3]
... We assume that the random vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi} has finite support. Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k=1,\ldots,K} index possible second stage realizations and let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_k} be the corresponding probabilities. With that, we could write down the deterministic equivalent of the stochastic program. This form is created by associating one set of second-stage decisions (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_k} ) to each realization of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi} , i.e., to each realization of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_k} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_k} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_k} . This large-scale deterministic counterpart of the original stochastic program is known as the extensive form:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \min c^T x + \sum_{k=1}^{K} p_k & q_k^T y_k \\ s.t. \qquad \quad Ax &= b \\ T_kx + W_{y_k} &= h_k, &k=1,...,K \\ x \ge 0, y_k &\ge 0, &k=1,...,K \\ \end{align} }
It is equivalent with the following formulation. The L-shape block structure of this extensive form gives rise to the name, L-shaped method.
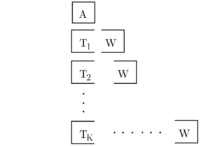
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{lccccccccccccc} \min & c^T x & + & p_1 q_1^T y_1 & + & p_2q_2^T y_2 & + & \cdots & + & p_K q_K^T y_K & & \\ s.t. & Ax & & & & & & & & & = & b \\ & T_1 x & + & W_1 y_1 & & & & & & & = & h_1 \\ & T_2 x & + & & & W_2y_2 & & & & & = & h_2 \\ & \vdots & & & & & & \ddots & & & & \vdots \\ & T_s x & + & & & & & & & W_K y_K & = & h_K \\ & x\ge 0 & , & y_1 \ge 0 & , & y_2 \ge 0 & & \ldots & & y_K \ge 0 \\ \end{array} }
L-Shaped Algorithm
Step 0. Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=s=v=0 } Step 1. Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v = v+1 } . Solve the following linear program (master program)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \min z =c^Tx &+ \theta\\ s.t. Ax &=b & & & (1) \\ D_{\ell}x &\ge d_{\ell}, & \ell = 1, \ldots, r & & (2)\\ E_{\ell}x + \theta &\ge e_{\ell}, & \ell = 1, \ldots, s & & (3) \\ x &\ge 0, & \theta \in \mathbb{R} & & (4) \end{align} }
Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x^k, \theta ^k)} be an optimal solution. If there is no constraint (3), set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta ^k = -\infty} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^k} is defined by the remaining constraints.
Step 2. For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k = 1,\ldots,K} solve the following linear program:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \min &w' = e^Tv^+ + e^Tv^- \\ s.t. &Wy + Iv^+ - Iv^- = h_k - T_kx^v \\ &y \ge 0, v^+ \ge 0, v^- \ge 0 \\ \end{align} }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^T = (1,\ldots,1)} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I} is the identity matrix. Until for some Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} the optimal value Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w' > 0} . In this case, let be the associated simplex multipliers and define
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{r+1} = (\sigma ^v)^T T_k}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{r+1} = (\sigma ^v)^T h_k}
to generate a constraint (called a feasibility cut) of type (2). Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=r+1} , add the constraint to the constraint set (2), and return to Step 1. If for all Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w' = 0} , go to Step 3.
Step 3: For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k=1,\ldots,K} solve the linear program
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \min &w = q^T_k y \\ s.t. &Wy = h_k - T_k x^v & & (4)\\ &y \ge 0 \end{align} }
Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi ^v_k} be the simplex multipliers associated with the optimal solution of Problem Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} of type (4). Define
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{s+1} = \sum_{k=1}^K p_k(\pi ^v_k)^T T_k}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e_{s+1} = \sum_{k=1}^K p_k(\pi ^v_k)^T h_k}
Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w^v = e_{s+1}-E_{s+1}x^v} . If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta ^v \ge w^v} , stop; Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^v} is an optimal solution. Otherwise, set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s = s+1} , add to the constraint set (3) and return to Step 1.
This method approximates Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{L}} using an outer linearization. This approximation is achieved by the master program (1)-(4). It finds a proposal Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} , then sent it to the second stage. Two types of constraints are sequentially added: (i) feasibility cuts (2) determining Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {x|\mathcal{L}(x) < +\infty}} and (ii) optimality cuts (3), which are linear approximations to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{L}} on its domain of finiteness.
Numerical Example
To illustrate the algorithm mentioned above, let's take a look at the following numerical example.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} z = \min 10{x_1} + 15&{x_2} + E_\xi (q_1y_1 + q_2y_2) \\ s.t. x_1 + x_2 &\le 12 \\ 6y_1 + 10y_2 &\le 60x_1 \\ 8y_1 + 5y_2 &\le 80x_2 \\ y_1 &\le d_1, y_2 \le d_2 \\ x_1 &\ge 4, x_2 \ge 2 \\ y_1, y_2 &\ge 0 \end{align} }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi ^T = (d_1, d_2, q_1, q_2)} has 0.4 probability to be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi _1 = (50, 10, -2.4, -2.8)} and 0.6 probability to be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi _2 = (30, 30, -2.8, -3.2)} .
We should note that in this case, as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \ge 0} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d \ge 0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_1, y_2 \ge 0} , the second stage is always feasible, which means Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \in K_2} always hold true. So we could skip the feasibility cuts (step 2) in all iterations. The L-shaped method iterations are shown below:
Iteration 1:
Step 1. With no Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta } , the master program is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = min\{10x_1 + 15x_2 | x_1 + x_2 \le 12, x_1 \ge 4, x_2 \ge 2\}} . Result is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^1 = (4, 2)^T} . Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta ^1 = -\infty } .
Step 2. No feasibility cut is needed.
Step 3.
- For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi = \xi _1} , solve:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w = min \{-2.4y_1 - 2.8y_2 | 6y_1 + 10y_2 \le 240, 8y_1 + 5y_2 \le 160, 0\le y_1 \le 50, 0\le y_2 \le 10 \} }
- The solution is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_1 = -61, y^T = (13.75, 10), \pi _1^T = (0, -0.3, 0, -1.3)}
- For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi = \xi _2} , solve:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w = min \{-2.8y_1 - 3.2y_2 | 6y_1 + 10y_2 \le 240, 8y_1 + 5y_2 \le 160, 0\le y_1 \le 30, 0\le y_2 \le 30 \} }
- The solution is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_2 = -83.84, y^T = (8, 19.2), \pi _2^T = (-0.232, -0.176, 0, 0)}
- Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_1 = (0, 0, 50, 10)^T, h_2 = (0, 0, 30, 30)^T } , we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e_1 = 0.4\cdot \pi _1^T \cdot h_1 + 0.6\cdot \pi _2^T \cdot h_2 = 0.4 \times (-13) + 0.6 \times (0) = -5.2}
- Here, the matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} is the same in these two scenarios, which is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} -60 & 0 \\ 0 & -80 \\ 0 & 0 \\ 0 & 0 \end{bmatrix}} . Therefore, we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_1 = 0.4\cdot \pi _1^T \cdot T + 0.6\cdot \pi _2^T \cdot T = 0.4 \times (0, 24) + 0.6 \times (13.92, 14.08) = (8.352, 18.048)}
- Thus, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w^1 = -5.2 - (8.352, 18.048) \cdot x^1 = -74.704 > \theta ^1 = -\infty } , we add the cut
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 8.352x_1 + 18.048x_2 + \theta \ge -5.2}
Iteration 2: Step 1. The master program is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = min\{10x_1 + 15x_2 + \theta | x_1 + x_2 \le 12, x_1 \ge 4, x_2 \ge 2, 8.352x_1 + 18.048x_2 + \theta \ge -5.2\}} . Result is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = -22.992, x^2 = (4, 8)^T, \theta ^2 = -182.992} .
Step 2. No feasibility cut is needed.
Step 3.
- For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi = \xi _1} , solve:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w = min \{-2.4y_1 - 2.8y_2 | 6y_1 + 10y_2 \le 240, 8y_1 + 5y_2 \le 640, 0\le y_1 \le 50, 0\le y_2 \le 10 \} }
- The solution is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_1 = -96, y^T = (40, 0), \pi _1^T = (-0.4, 0, 0, 0)}
- For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi = \xi _2} , solve:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w = min \{-2.8y_1 - 3.2y_2 | 6y_1 + 10y_2 \le 240, 8y_1 + 5y_2 \le 640, 0\le y_1 \le 30, 0\le y_2 \le 30 \} }
- The solution is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_2 = -103.2, y^T = (30, 6), \pi _2^T = (-0.32, 0, -0.88, 0)}
- Thus,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e_2 = 0.4\cdot \pi _1^T \cdot h_1 + 0.6\cdot \pi _2^T \cdot h_2 = 0.4 \times (0) + 0.6 \times (-26.4) = -15.84}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_2 = 0.4\cdot \pi _1^T \cdot T + 0.6\cdot \pi _2^T \cdot T = 0.4 \times (24, 0) + 0.6 \times (19.2, 0) = (21.12, 0)}
- Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_2 = -15.84 - 21.12 \cdot 4 = -100.32 > -182.992, add the cut :<math>21.12x_1 + \theta \ge -15.84}
The setting is summarized below:
A farmer plans to raise wheat, corn, and sugar beets with 500 acres of land. The three crops' planting costs, selling prices, and minimum quantities required are listed in the table below.
| Wheat | Corn | Sugar Beets | |
|---|---|---|---|
| Planting cost ($/acre) | 150 | 230 | 260 |
| Selling price ($/T) | 170 | 150 | 36 under 6000T, 10 above 6000T |
| Purchase price ($/T) | 238 | 210 | |
| Minimum requirement (T) | 200 | 240 |
The naive version of the problem ignores the weather's effect on crops' yield, simply assuming that the yield of each crop per acre is determined. With that, the problem becomes a linear program, which could be solved by any LP solvers. However, this method fails to identify yield's high dependence on weather conditions. To address this problem, we assume that crop yields are random variables affected by the weather. For simplicity, we assume there are three possible climatic conditions: good, fair, and bad. Crop yields vary under different conditions. The specific yields are listed below:
| Climatic Condition | Wheat (T/acre) | Corn (T/acre) | Sugar Beets (T/acre) |
|---|---|---|---|
| Good | 3 | 3.6 | 24 |
| Fair | 2.5 | 3 | 20 |
| Bad | 2 | 2.4 | 16 |
From that, we can obtain the two-stage stochastic program for the farmer's problem. Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} s &= 1, 2, 3 \text{ corresponding to good, fair, or bad weather conditions, respectively} \\ i &= 1,\ldots, 4 \text{ corresponding to wheat, corn, sugar beets (under 6000 tons), and sugar beets (above 6000 tons)} \\ x_i (i = 1,\ldots, 4) &= \text{ acres of land devoted to each crops} \\ w_{is} (i = 1,\ldots, 4, s = 1, 2, 3) &= \text{ tons of each crop sold under each weather condition} \\ y_{is} (i = 1, 2, s = 1, 2, 3) &= \text{ tons of wheat and corn purchased under each weather condition} \\ \end{align} }
If the three scenarios all have a probability of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac13} to happen, the farmer's problem reads as follows:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \min 150{x_1} &+ 230{x_2} + 260{x_3} \\ &- \frac13(170w_{11} - 238y_{11} + 150w_{21} - 210y_{21} + 36w_{31} + 10w_{41}) \\ &- \frac13(170w_{12} - 238y_{12} + 150w_{22} - 210y_{22} + 36w_{32} + 10w_{42}) \\ &- \frac13(170w_{13} - 238y_{13} + 150w_{23} - 210y_{23} + 36w_{33} + 10w_{43}) \\ s.t. x_{1} + x_{2} + x_{3} &\le 500 \\ 3x_{1} + y_{11} - w_{11} &\ge 200 \\ 3.6x_{2} + y_{21} - w_{21} &\ge 240 \\ w_{31} + w_{41} &\le 24x_{3}, w_{31} \le 6000 \\ 2.5x_{1} + y_{12} + w_{12} &\ge 200 \\ 3x_{2} + y_{22} - w_{22} &\ge 240 \\ w_{32} + w_{42} &\le 20x_{3} \\ w_{32} &\le 6000 \\ 2x_{1} + y_{13} - w_{13} &\ge 200 \\ 2.4x_{2} + y_{23} - w_{23} &\ge 240 \\ w_{33} + w_{43} &\le 16x_{3} \\ w_{33} &\le 6000 \\ x, y, w &\ge 0 \end{align} }
Results from the two models suggest that when yields are high a small surface is sufficient to meet the minimum production requirement. However, when yields are low larger surface areas are needed to meet the minimum production requirement. In fact, with low yields corn must be purchased from the market to meet requirements. Thus, the key takeaway is that the optimal solution is sensitive to changes in yields. The farmer would benefit tremendously if they had access to the weather forecast. But, given the absence of perfect information, the farmer must make a decision based on the existing data.
Among all the three crops, i.e., wheat, corn, and sugar beets, making a decision pertaining to sugar beets cultivation seems difficult for the farmer. On the one hand, if the farmer were to dedicate large surface areas to sugar beet cultivation the farmer would certainly meet the requirement and sell at the quota, but would also have to sell the excess amount of sugar beets at the unfavorable price. On the other hand, if small surface areas were dedicated to sugar beet cultivation, then the farmer would miss the opportunity of selling at the quota (favorable) price. In the stated situation, the farmer realizes that a perfect decision cannot be taken - a decision that would work in all possible scenarios. The farmer would like to evaluate the benefits and losses of every decision at each stage, and to do so adopts the two-stage stochastic linear programming approach.
In the first stage, decisions that are to be taken ‘now’, are those pertaining to the land assignment of each crop. Let land assignment to wheat be ‘x1’, land assignment to corn be ‘x2’ and land assignment to sugar beets be ‘x3’. While decisions pertaining to sales and purchases depend on the yield. The second-stage variables can be indexed based on scenarios, where ‘s1’ corresponds to above-average yields, ‘s2’ corresponds to average yields and ‘s3’ corresponds to below-average yields. If the farmer seeks to maximize long-run profit then the three defined scenarios have an equal probability of 1/3. Given how explicitly the second-stage variables have been defined, this problem can be considered as an extensive form of stochastic programming. Having stated the approach, the problem can be formulated as given below:
| Wheat | Corn | Sugar beets | ||
| First decision | Area in terms of Acres | 170 | 80 | 250 |
| s=1 (above average yield) | Yield (t) | 510 | 288 | 6000 |
| Sales (t) | 310 | 48 | 6000 (favorable price) | |
| Purchase (t) | - | - | - | |
| s=2 (average yield) | Yield (t) | 425 | 240 | 5000 |
| Sales (t) | 225 | - | 5000 (favorable price) | |
| Purchase (t) | - | - | - | |
| s=3 (below average yield) | Yield (t) | 340 | 192 | 4000 |
| Sales (t) | 140 | - | 4000(favorable price) | |
| Purchase (t) | - | 48 | ||
| Overall profit ($) | 108,390 | |||
Table A: Solution from the two-stage linear stochastic model.
The solution showcases a key aspect, under uncertainty finding a solution that works for all circumstances is quite not possible. For one, the farmer would always have to decide on the trade-off between selling some sugar beets at an unfavorable price or having some unused quota. Such a predicament would never arise if the farmer had access to a perfect weather forecast. Given the uncertainty, stochastic programming helps model balanced decisions
Applications
Apart from the process industry, two-stage linear stochastic programming finds application in other fields as well. For instance, in the optimal design of distributed energy systems, there are various uncertainties that need to be considered. Uncertainty is related to aspects such as demand and supply of energy, economic factors like unit investment cost and energy price, and uncertainty related to technical parameters like efficiency. Zhou et al. [9], developed a two-stage stochastic programming model for the optimal design of a distributed energy system with a stage decomposition-based solution strategy. The authors accounted for both demand and supply uncertainty. They used the genetic algorithm on the first stage variables and the Monte Carlo method on the second-stage variables.
Another application of the two-stage linear stochastic programming is in the bike-sharing system (BSS). The system needs to ensure that bikes are available at all stations per the given demand. To ensure this balance, redistribution trucks are used to transfer bikes from one bike surplus station to a bike deficient station. Such a problem is referred to as the bike repositioning problem (BRS) in the aforementioned system. [10] Another challenge related to BRP is the aspect related to the holding cost of the depot. While transferring bikes from one station to another they could get damaged or be lost in the process which could lead to an imbalance between demand and supply in the BSS. As for bikes that cannot be balanced among the stations of the BSS are either placed back at the depot at increase the holding cost of the depot. To address the stated concerns, Tang et al [10], developed a two-stage stochastic program that would capture the uncertainty related to redistribution of demand within the system. In the first stage, before the realization of redistribution demand, a decision regarding routing was made. In the second stage, decisions regarding loading/unloading at each station and depot are made. Holding cost is incorporated into the model, such that the model’s primary objective is to determine the best routes of the repositioning truck and the optimal loading/unloading quantities at each station and depot. The model is framed to minimize the expected total sum of transportation cost, the penalty cost of all stations, and the holding cost of the depot.
Conclusion
From the previous examples, it is evident that two-stage linear stochastic programming finds applicability across many areas, such as the petrochemical, pharmaceutical industry, carbon capture, and energy storage among others. [3] Stochastic programming can primarily be used to model two types of uncertainties: 1) exogenous uncertainty, which is the most widely considered one, and 2) endogenous uncertainty, where realization regarding uncertainty depends on the decision taken. The main challenge, with respect to stochastic programming, is that the type of problems that can be solved is limited. An ‘ideal’ problem would be multi-stage stochastic mixed-integer nonlinear programming under both exogenous and endogenous uncertainty with an arbitrary probability distribution that is stagewise dependent. [3] However, current algorithms, in terms of development and computation resources, are still limited with respect to the ability to solve the ‘ideal’ problem.
References
- ↑ Li, C., & Grossmann, I. E. (2021). A review of stochastic programming methods for optimization of process systems under uncertainty. Frontiers in Chemical Engineering, 2. https://doi.org/10.3389/fceng.2020.622241
- ↑ 2.0 2.1 2.2 2.3 2.4 “Integration of Scheduling and Dynamic Optimization of Batch Processes under Uncertainty: Two-Stage Stochastic Programming Approach and Enhanced Generalized Benders Decomposition Algorithm,”Yunfei Chu and Fengqi You, Industrial & Engineering Chemistry Research 2013 52 (47), 16851-16869 DOI: 10.1021/ie402621t
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 Li Can, Grossmann Ignacio E., “A Review of Stochastic Programming Methods for Optimization of Process Systems Under Uncertainty,” Frontiers in Chemical Engineering 2021, Vol. 2; DOI: 10.3389/fceng.2020.622241
- ↑ 4.0 4.1 “A Tutorial on Stochastic Programming,” Shapiro, Alexander and Philpott, Andy
- ↑ Powell, W. B. (2019). A unified framework for stochastic optimization. European Journal of Operational Research, 275(3), 795-821.
- ↑ Barik, S.K., Biswal, M.P. & Chakravarty, D. Two-stage stochastic programming problems involving interval discrete random variables. OPSEARCH 49, 280–298 (2012). https://doi.org/10.1007/s12597-012-0078-1
- ↑ 7.0 7.1 Soares, J., Canizes, B., Ghazvini, M. A. F., Vale, Z., & Venayagamoorthy, G. K. (2017). Two-stage stochastic model using benders’ decomposition for large-scale energy resource management in smart grids. IEEE Transactions on Industry Applications, 53(6), 5905-5914.
- ↑ 8.0 8.1 Cite error: Invalid
<ref>tag; no text was provided for refs named:10 - ↑ Zhe Zhou, Jianyun Zhang, Pei Liu, Zheng Li, Michael C. Georgiadis, Efstratios N. Pistikopoulos, “A two-stage stochastic programming model for the optimal design of distributed energy systems,” Applied Energy, Volume 103, 2013, Pages 135-144, ISSN 0306-2619, https://doi.org/10.1016/j.apenergy.2012.09.019.
- ↑ 10.0 10.1 Qiong Tang, Zhuo Fu, Dezhi Zhang, Hao Guo, Minyi Li, "Addressing the Bike Repositioning Problem in Bike Sharing System: A Two-Stage Stochastic Programming Model", Scientific Programming, vol. 2020, Article ID 8868892, 12 pages, 2020.https://doi.org/10.1155/2020/8868892

