Adam: Difference between revisions
| Line 5: | Line 5: | ||
== Theory == | == Theory == | ||
Adam is a combination of two gradient descent methods which are explained below | Adam is a combination of two gradient descent methods, Momentum, and RMSP which are explained below; | ||
=== Momentum: === | === Momentum: === | ||
This is an optimization algorithm that takes into consideration the 'exponentially weighted average' and accelerates the gradient descent. It is an extension of the gradient descent optimization algorithm. | This is an optimization algorithm that takes into consideration the 'exponentially weighted average' and accelerates the gradient descent. It is an extension of the gradient descent optimization algorithm. | ||
The Momentum algorithm is solved in two parts. The first is to calculate the change | The Momentum algorithm is solved in two parts. The first is to calculate the position change and the second is to update the old position. The change in the position is given by; | ||
'''''update = α * m_t''''' | '''''update = α * m_t''''' | ||
The new position or weights at time t is given by | The new position or weights at time t is given by; | ||
'''''w_t+1 = w_t - update''''' | '''''w_t+1 = w_t - update''''' | ||
Here in the above equation ''α (Step Size)'' is the Hyperparameter that controls the movement in the search space, which is also called as the learning rate where | Here in the above equation ''α (Step Size)'' is the Hyperparameter that controls the movement in the search space, which is also called as the learning rate where; | ||
'''''m_t = β * m_t - 1 + (1 - β) * (∂L / ∂w_t)''''' | '''''m_t = β * m_t - 1 + (1 - β) * (∂L / ∂w_t)''''' | ||
| Line 29: | Line 29: | ||
RMSP is an adaptive optimization algorithm that is an improved version of AdaGrad. In AdaGrad we take the cumulative summation of squared gradients but, in RMSP we take the 'exponential average'. | RMSP is an adaptive optimization algorithm that is an improved version of AdaGrad. In AdaGrad we take the cumulative summation of squared gradients but, in RMSP we take the 'exponential average'. | ||
It is given by | It is given by; | ||
'''''w_t+1 = w_t - (αt / (vt + e) ^ 1/2) * (∂L / ∂w_t)''''' | '''''w_t+1 = w_t - (αt / (vt + e) ^ 1/2) * (∂L / ∂w_t)''''' | ||
where | where; | ||
'''''vt = βvt - 1 + (1 - β) * (∂L / ∂w_t) ^ 2''''' | '''''vt = βvt - 1 + (1 - β) * (∂L / ∂w_t) ^ 2''''' | ||
Here | Here; | ||
Aggregate of gradient at ''t = m_t'' | Aggregate of gradient at ''t = m_t'' | ||
| Line 64: | Line 64: | ||
'''''m_t = β1 * m_t - 1 + (1 - β1) * (∂L / ∂w_t) and vt = β2vt - 1 + (1 - β2) * (∂L / ∂w_t) ^ 2''''' | '''''m_t = β1 * m_t - 1 + (1 - β1) * (∂L / ∂w_t) and vt = β2vt - 1 + (1 - β2) * (∂L / ∂w_t) ^ 2''''' | ||
Initially, both ''mt'' and ''vt'' are set to 0. Both tend to be more biased towards 0 as β1 and β2 are equal to 1. By computing bias-corrected ''m_''t and ''vt'', this problem is corrected by the Adam optimizer. The equations are as follows | Initially, both ''mt'' and ''vt'' are set to 0. Both tend to be more biased towards 0 as β1 and β2 are equal to 1. By computing bias-corrected ''m_''t and ''vt'', this problem is corrected by the Adam optimizer. The equations are as follows; | ||
'''''m'_t = m_t / (1 - β1 ^ t)''''' | '''''m'_t = m_t / (1 - β1 ^ t)''''' | ||
| Line 70: | Line 70: | ||
'''''v't = vt / (1 - β2 ^ t)''''' | '''''v't = vt / (1 - β2 ^ t)''''' | ||
Now as we are getting used to gradient descent after every iteration and hence it remains controlled and unbiased. Now substitute the new parameters in place of the old ones. We get | Now as we are getting used to gradient descent after every iteration and hence it remains controlled and unbiased. Now substitute the new parameters in place of the old ones. We get; | ||
'''''w_t+1 = w_t - m'_t ( α / v't^1/2 + e)''''' | '''''w_t+1 = w_t - m'_t ( α / v't^1/2 + e)''''' | ||
| Line 103: | Line 103: | ||
|} | |} | ||
The hypothesis function is | The hypothesis function is; | ||
<math>f_\theta(x) = \theta_0 + \theta_1 x.</math> | <math>f_\theta(x) = \theta_0 + \theta_1 x.</math> | ||
The cost function is | The cost function is; | ||
<math> J({\theta}) = \frac{1}{2}\sum_i^n \big(f_\theta(x_i) - y_i \big)^2 | <math> J({\theta}) = \frac{1}{2}\sum_i^n \big(f_\theta(x_i) - y_i \big)^2 </math> | ||
The optimization problem is defined as, we must find the values of theta which help to minimize the objective function mentioned below | The optimization problem is defined as, we must find the values of theta which help to minimize the objective function mentioned below; | ||
<math> \mathrm{argmin}_{\theta} \quad \frac{1}{n}\sum_{i}^n \big(f_\theta(x_i) - y_i \big) ^2 </math> | <math> \mathrm{argmin}_{\theta} \quad \frac{1}{n}\sum_{i}^n \big(f_\theta(x_i) - y_i \big) ^2 </math> | ||
The cost function with respect to the weights <math>\theta_0</math> and <math>\theta_1</math> are | The cost function with respect to the weights <math>\theta_0</math> and <math>\theta_1</math> are; | ||
<math> \frac{\partial J(\theta)}{\partial \theta_0} = \big(f_\theta(x) - y \big) </math><br/> | <math> \frac{\partial J(\theta)}{\partial \theta_0} = \big(f_\theta(x) - y \big) </math><br/> | ||
| Line 121: | Line 121: | ||
The initial values of <math>{\theta}</math> will be set to [10, 1] and the learning rate <math>\alpha</math>, is set to 0.01 and setting the parameters <math>\beta_1</math>, <math>\beta_2</math>, and e as 0.94, 0.9878 and 10^-8 respectively. Starting from the first data sample the gradients are | The initial values of <math>{\theta}</math> will be set to [10, 1] and the learning rate <math>\alpha</math>, is set to 0.01 and setting the parameters <math>\beta_1</math>, <math>\beta_2</math>, and e as 0.94, 0.9878 and 10^-8 respectively. Starting from the first data sample the gradients are; | ||
<math> \frac{\partial J(\theta)}{\partial \theta_0} = \big((10 + 1\cdot 60 - 76 \big) = -6 </math><br /> | <math> \frac{\partial J(\theta)}{\partial \theta_0} = \big((10 + 1\cdot 60 - 76 \big) = -6 </math><br /> | ||
| Line 129: | Line 129: | ||
<math> m_1 = 0.94 \cdot 0 + (1-0.94) \cdot \begin{bmatrix} -6\\ -360 \end{bmatrix} = \begin{bmatrix} -0.36\\ -21.6\end{bmatrix} </math> <br /> | <math> m_1 = 0.94 \cdot 0 + (1-0.94) \cdot \begin{bmatrix} -6\\ -360 \end{bmatrix} = \begin{bmatrix} -0.36\\ -21.6\end{bmatrix} </math> <br /> | ||
<math> v_1 = 0.9878\cdot 0 + (1-0.9878) \cdot \begin{bmatrix} -6^2\\-360^2 \end{bmatrix} = \begin{bmatrix} 0.4392\\ 1581.12\end{bmatrix} | <math> v_1 = 0.9878\cdot 0 + (1-0.9878) \cdot \begin{bmatrix} -6^2\\-360^2 \end{bmatrix} = \begin{bmatrix} 0.4392\\ 1581.12\end{bmatrix} </math> <br /> | ||
The new bias-corrected values of <math>m_1</math> and <math>v_1</math> are | The new bias-corrected values of <math>m_1</math> and <math>v_1</math> are; | ||
<math> \hat{m}_1 = \begin{bmatrix} -0.36\\ -21.6\end{bmatrix} \frac{1}{ (1-0.94^1)} = \begin{bmatrix} -6\\-360\end{bmatrix}</math> <br /> | <math> \hat{m}_1 = \begin{bmatrix} -0.36\\ -21.6\end{bmatrix} \frac{1}{ (1-0.94^1)} = \begin{bmatrix} -6\\-360\end{bmatrix}</math> <br /> | ||
<math> \hat{v}_1 = \begin{bmatrix} 0.4392\\ 1581.12\end{bmatrix} \frac{1} {(1-0.9878^1)} = \begin{bmatrix} 36\\129600\end{bmatrix} | <math> \hat{v}_1 = \begin{bmatrix} 0.4392\\ 1581.12\end{bmatrix} \frac{1} {(1-0.9878^1)} = \begin{bmatrix} 36\\129600\end{bmatrix} </math> <br /> | ||
Finally, the weight update is | Finally, the weight update is; | ||
<math> \theta_0 = 10 - 0.01 \cdot -6 / (\sqrt{36} + 10^{-8}) = 10.01 </math> <br/> | <math> \theta_0 = 10 - 0.01 \cdot -6 / (\sqrt{36} + 10^{-8}) = 10.01 </math> <br/> | ||
Revision as of 18:16, 15 December 2021
Author: Akash Ajagekar (SYSEN 6800 Fall 2021)
Introduction
Adam optimizer is the extended version of stochastic gradient descent which has a broader scope in the future for deep learning applications in computer vision and natural language processing. Adam was first introduced in 2014. It was first presented in a famous conference for deep learning researchers called ICMR 2015. It is an optimization algorithm that can be an alternative for the stochastic gradient descent process. The name is derived from adaptive moment estimation. The optimizer is called Adam because uses estimations of first and second moments of gradient to adapt the learning rate for each weight of the neural network. The name of the optimizer is Adam; it is not an acronym. Adam is proposed as the most efficient stochastic optimization which only requires first-order gradients where memory requirement is too less. Before Adam many adaptive optimization techniques were introduced such as AdaGrad, RMSP which have good performance over SGD but in some cases have some disadvantages such as generalizing performance which is worse than that of the SGD in some cases. So, Adam was introduced which is better in terms of generalizing performance.
Theory
Adam is a combination of two gradient descent methods, Momentum, and RMSP which are explained below;
Momentum:
This is an optimization algorithm that takes into consideration the 'exponentially weighted average' and accelerates the gradient descent. It is an extension of the gradient descent optimization algorithm.
The Momentum algorithm is solved in two parts. The first is to calculate the position change and the second is to update the old position. The change in the position is given by;
update = α * m_t
The new position or weights at time t is given by;
w_t+1 = w_t - update
Here in the above equation α (Step Size) is the Hyperparameter that controls the movement in the search space, which is also called as the learning rate where;
m_t = β * m_t - 1 + (1 - β) * (∂L / ∂w_t)
In the above equations, m_t and m_t-1 are aggregates of gradients at time t and aggregate of the gradient at time t-1.
According to [1] Momentum has the effect of dampening down the change in the gradient and, in turn, the step size with each new point in the search space.
Root Mean Square Propagation (RMSP):
RMSP is an adaptive optimization algorithm that is an improved version of AdaGrad. In AdaGrad we take the cumulative summation of squared gradients but, in RMSP we take the 'exponential average'.
It is given by;
w_t+1 = w_t - (αt / (vt + e) ^ 1/2) * (∂L / ∂w_t)
where;
vt = βvt - 1 + (1 - β) * (∂L / ∂w_t) ^ 2
Here;
Aggregate of gradient at t = m_t
Aggregate of gradient at t - 1 = m_t - 1
Weights at time t = w_t
Weights at time t + 1 = w_t + 1
αt = learning rate(Hyperparameter)
∂L = derivative of loss function
∂w_t = derivative of weights at t
β = Average parameter
e = constant
But as we know these two optimizers explained below have some problems such as generalizing performance. The article [2] tells us that Adam takes over the attributes of the above two optimizers and build upon them to give more optimized gradient descent.
Algorithm
Taking the equations used in the above two optimizers
m_t = β1 * m_t - 1 + (1 - β1) * (∂L / ∂w_t) and vt = β2vt - 1 + (1 - β2) * (∂L / ∂w_t) ^ 2
Initially, both mt and vt are set to 0. Both tend to be more biased towards 0 as β1 and β2 are equal to 1. By computing bias-corrected m_t and vt, this problem is corrected by the Adam optimizer. The equations are as follows;
m'_t = m_t / (1 - β1 ^ t)
v't = vt / (1 - β2 ^ t)
Now as we are getting used to gradient descent after every iteration and hence it remains controlled and unbiased. Now substitute the new parameters in place of the old ones. We get;
w_t+1 = w_t - m'_t ( α / v't^1/2 + e)
Performance
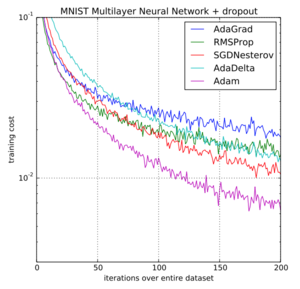
Adam optimizer gives much higher performance results than the other optimizers and outperforms by a big margin for a better-optimized gradient. The diagram below is one example of a performance comparison of all the optimizers.
Numerical Example
Let's see an example of Adam optimizer. A sample dataset is shown below which is the weight and height of a couple of people. We have to predict the height of a person based on the given weight.
| Weight | 60 | 76 | 85 | 76 | 50 | 55 | 100 | 105 | 45 | 78 | 57 | 91 | 69 | 74 | 112 |
| Height | 76 | 72.3 | 88 | 60 | 79 | 47 | 67 | 66 | 65 | 61 | 68 | 56 | 75 | 57 | 76 |
The hypothesis function is;
The cost function is;
The optimization problem is defined as, we must find the values of theta which help to minimize the objective function mentioned below;
The cost function with respect to the weights and are;
The initial values of will be set to [10, 1] and the learning rate , is set to 0.01 and setting the parameters , , and e as 0.94, 0.9878 and 10^-8 respectively. Starting from the first data sample the gradients are;
Here and are zero, and are calculated as
The new bias-corrected values of and are;
Finally, the weight update is;
The procedure is repeated until the values of the weights are converged.
Applications
The Adam optimization algorithm is the replacement optimization algorithm for SGD for training DNN. According [3] to Adam combines the best properties of the AdaGrad and RMSP algorithms to provide an optimization algorithm that can handle sparse gradients on noisy problems. Research has shown that Adam has demonstrated superior experimental performance over all the other optimizers such as AdaGrad, SGD, RMSP etc.[ref] Further research is going on Adaptive optimizers for Federated Learning and their performances are being compared. Federated Learning is a privacy preserving technique which is an alternative for Machine Learning where data training is done on the device itself without sharing it with the cloud server.
Conclusion
Research has shown that Adam has demonstrated superior experimental performance over all the other optimizers such as AdaGrad, SGD, RMSP etc in DNN.[ref]. This type of optimizers are useful for large datasets. As we know this optimizer is a combination of Momentum and RMSP optimization algorithms. This method is pretty much straightforward, easy to use and requires less memory. Also we have shown a example where all the optimizers are compared and the results are shown with the help of the graph. Overall it is a robust optimizer and well suited for non-convex optimization problems in the field of Machine Learning and Deep Learning [4].
References
- ↑ Deep Learning (Adaptive Computation and Machine Learning series)
- ↑ https://www.geeksforgeeks.org/intuition-of-adam-optimizer/ Intuition of Adam Optimizer
- ↑ https://machinelearningmastery.com/adam-optimization-algorithm-for-deep-learning/#:~:text=Specifically%2C%20you%20learned%3A,sparse%20gradients%20on%20noisy%20problems. Gentle Introduction to the Adam Optimization Algorithm for Deep Learning
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs named:0






















