Branch and bound (BB) for MINLP
Introduction
The arrangements of conventional design problems into programming models make room to their definition and execution of their general option solution. Problems organized as a set of continuous variables with binary integer variables are represented by MINLP models. The continuous variables are restricted to defined constraints while the binary variables shows if a design option is constructed or not. Branch and bound is a method used to solve Mixed Integer Non-Linear Programming (MINLP) models. There is a difference in the exact steps of the algorithm; however, the initial method created in 2000 by Ioannis Akrotirianakis, Istvan Maros, and Berc Rustem uses a general arrangement of the branch and bound that has iterative nature of the outer estimation (Altherr et al., 2019). The general efficiency of the branch and bound algorithm is improved by adding Gomory mixed-integer cuts as an alternative to branching to reduce the number of nodes and Non-Liner Programming (NLP) problems needed to solve the MINLP. The algorithm for branch and bound (BB) method was originally proposed by A.H. Land and A.G. Doig in 1960 for discrete programming (Jiyao et al., 2014).
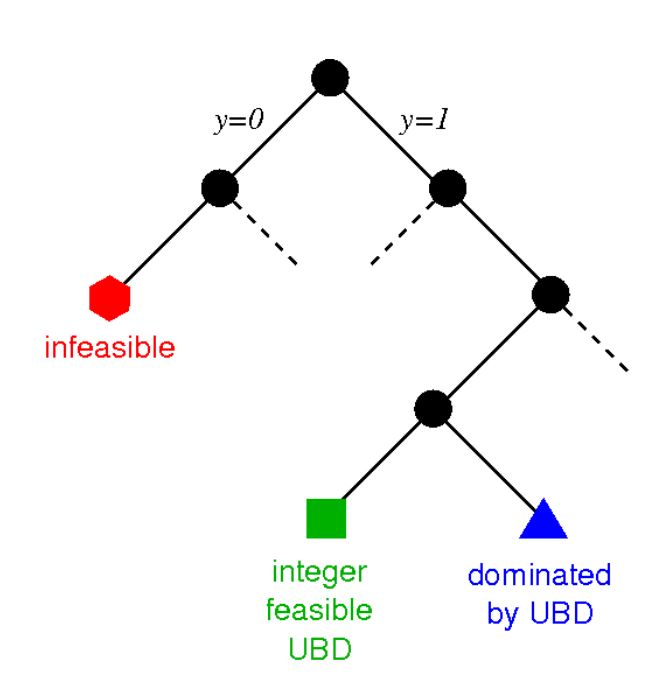
Algorithmic Discussion
Relax and search are the basic performances common to algorithms when finding a solution to MINLP. The difference in algorithms occurs depending on how these performances are executed. In convex MINLPs, the most unaffected relaxation is to ignore the totality constraints . This results in a nonlinear program (NLP) that is solved to global optimality to produce a lower bound on the optimal solution value . When the solution is relaxed to have , then is supposed to be the optimal answer of MINLP; otherwise, there is a with (Cacchiani & D’Ambrosio, 2017). The search is continuous when it comes to branch and bound whereby it creates two sub-problems; one with the additional constraint and the other one with additional constraint . The same procedure is used to solve these two sub-problems, and it results in search-tree sub-problems that are investigated.
On the other hand, when or are not convex functions, then quality algorithms for handling NLP will assure that convergence will occur to a local minimum only. Therefore, the simple solution will not be capable of providing a lower bound on . In this scenario of nonconvex MINLP, an additional relaxation procedure is needed. Generally, relaxation depends on the decomposition of a nonlinear function into elements and for every element, a "convex envelope" relaxation is developed (Cacchiani & D’Ambrosio, 2017). Branch and bound is again used in relaxation where there is the additional complexity that continuous variables x can need branching to better the convex relaxation of the initial nonconvex function. While solving this class, a difference occurs in the method in which relaxation is developed.
Let , and be convex as well as continuous differentiable. To form a general MINLP problem that will be solved using the branch and bound method it will be done as shown below:
The branch and bound method usually follows the outer approximation for MINLP when incorporating Gomory cuts to reduce the search space for the problem (Jaber et al., 2021). The initial developer presented the algorithm as shown in the various methods below.
Initialization: Search Tree Root Value
Step 1 Upper bound = Lower bound =
Step 2: Initialize
Initialization of binary variables () is the first step of the branch and bound method, and the step defines each with a finite beginning value 0 or 1. Another way of achieving initialization is by solving a simple NLP setting .
Using to solve NLP
If NLP is feasible
→ solve . The product of this will be a new upper bound to the initial problem. Then move to step 3
Else NLP is not feasible
→ when the original set of values for is selected; select a new ().
Steps 1 and 2 are supposed to be repeated until a feasible solution is found. Move to step 3.
The result from NLP should be the initial feasible solution and whereby . But when relaxed NLP is infeasible, the MINLP problem becomes infeasible.
Solving MINLP
Using and gotten from NLP, constraints and linearized objective is solved using the following equations:
When MINLP is solved, the product is a new set of () and (). These new () and () are the branch's root and bound search tree.
Solving Nodes
This starts by selecting an unsolved node, and in cases where no nodes are left, the problem is solved. The optimal solution found is . If all , it becomes a new incumbent and Z that will be obtained from the set of and will be the current optimal solution (Jaber et al., 2021). When and are used to solve each unsolved node, the equation below is used:
Using the previous feasible solution to solve MINLP in this form
Start with excluding root will become
T is set with all indices of the solution tree in which NLP for is feasible.
+
Such that S is the set that has all indices of solution whereby NLP is infeasible
This constraint is a representation of the Gomory cut produced as algorithm runs. This line reduces the feasible region of the initial problem, which is . The final product of solving MINLP is a new set of and .
Numerical Solution
Consider the optimization problem with the following objective function and constraints
To verify if [0.05, 0.5] is optimal relaxed solution (with continuous variables). This is the root node lower bound for the integer solution objective and beginning point for the branch and bound.
is positive definite for minimum
Or
Principle minors
Application
The branch and bound method can be used in many programming problems because it converts them to mixed-integer nonlinear programming and solves them using the branch and bound method (Zhang et al., 2020). Besides the mathematical application, it can be used in various engineering and design issues.
Mathematical Problem
Mathematically, the Branch and bound method for MINLP is commonly used to solve the travelling salesman problem. In 1991, Padberg and Rinaldi created a solution to a large-scale symmetric travelling salesman issue utilizing the branch and cut method (Jaber et al., 2021). MINLP problems that can be solved using branch and bound algorithms are; biological models, scheduling and network design (involving finding location).
Industrial Application
Designing a thermal insulation layer for the huge hadron collider requires the branch and bound method for MINLP. Series of heat intercepts as well as surrounding insulators use thermal insulation to reduce the power needed to keep the heat intercepts at specific temperatures (Cacchiani & D’Ambrosio, 2017). These issues come up in planning superconducting magnetic energy storage systems as well as being utilized in large huge collider projects. Designers select the maximum number of intercepts; the discrete set of materials is selected depending on the thickness and area of every intercept and the intercepted material. The thermal conductivity as well as total mass of the insulation system depend on the selected material (Cacchiani & D’Ambrosio, 2017). Nonlinear functions on the model are needed for accuracy purposes like stress constraints and heat flow between the intercept and thermal expansion. Integer variables are utilized to model the discrete choice of the type of material to utilize in every layer. When branch and bound for MINLP is used, it identifies better materials compared to using other methods. Branch and bound is an improvement because of the capability to handle a more significant amount of intercepts than other methods (Altherr et al., 2019). Therefore, most designers tend to apply this method to ensure that they have an optimal solution.
Conclusion
In general, the branch and bound method follows a scheme that grows exponentially because variables are added to the initial design problem. When Gomory cuts are added, they allow bounds to tighten by decreasing the number of feasible nodes tested and permitting the solver to converge on the optimal solutions with minimum iterations. However, it takes time to form inequalities to production cuts, which can slow down the real resolution of the MINLP problem. Due to this, it should be noted that the larger the problem, the more significant the cuts become.
References
1. Altherr, L., Leise, P., Pfetsch, M., & Schmitt, A. (2019). Resilient layout, design and operation of energy-efficient water distribution networks for high-rise buildings using MINLP. Optimization And Engineering, 20(2), 605-645. https://doi.org/10.1007/s11081-019-09423-8
2. Cacchiani, V., & D’Ambrosio, C. (2017). A branch-and-bound based heuristic algorithm for convex multi-objective MINLPs. European Journal Of Operational Research, 260(3), 920-933. https://doi.org/10.1016/j.ejor.2016.10.015
3. Jaber, A., Lafon, P., & Younes, R. (2021). A branch-and-bound algorithm based on NSGAII for multi-objective mixed integer nonlinear optimization problems. Engineering Optimization, 1-19. https://doi.org/10.1080/0305215x.2021.1904918
4. Zhang, Y., Sahinidis, N., Nohra, C., & Rong, G. (2020). Optimality-based domain reduction for inequality-constrained NLP and MINLP problems. Journal Of Global Optimization, 77(3), 425-454. https://doi.org/10.1007/s10898-020-00886-z





![{\displaystyle y_{j}\geq [y_{j}^{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/275a6f294ececa312763e983db452b60fe2db29b)
![{\displaystyle y_{j}\leq [y_{j}^{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3763c8e4cf712ffb4e9f1e1b919154080c14d0fb)




















































