Branch and cut
Author: Lindsay Siegmundt, Peter Haddad, Chris Babbington, Jon Boisvert, Haris Shaikh (SysEn 6800 Fall 2020)
Steward: Wei-Han Chen, Fengqi You
Introduction
The Branch and Cut is a methodology that is used to optimize linear problems that are integer based. This concept is comprised of two known optimization methodologies - branch and bound and cutting planes. Utilizing these tools allows for the Branch and Cut to be successful by increasing the relaxation and decreasing the lower bound. The ultimate goal of this technique is to minimize the amount of nodes.
Methodology & Algorithm
Methodology - Haris
Most infeasible branching:
Most infeasible branching is a very popular method that picks the variable with fractional part closest to 0:5, i.e., si = 0:5 − |xAi − xAi− 0:5|. Most infeasible branching picks a variable where the least tendency can be recognized to which side the variable should be rounded. However, the performance of this method is not any superior to the rule of selecting a variable randomly.
Strong Branching:
For each fractional variable, strong branching tests the dual bound increase by computing the LP relaxations result from the branching on that variable. As a branching variable for the current for the
current node, the variable that leads to the largest increases is selected. Despite its obvious simplicity, strong branching is so far the most powerful branching technique in terms of the number of nodes available in the B&B tree, this effectiveness can however be accomplished only at the cost of computation.
Pseudo cost:
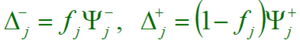
Another way to approximate a relaxation value is by utilizing a pseudo cost method. The pseudo-cost of a variable is an estimate of the per unit change in the objective function from making the value of the variable to be rounded up or down. For each variable we choose variable with the largest estimated LP objective gain.
Algorithm - PeterBranch and Cut for is a variation of the Branch and Bound algorithm. Branch and Cut incorporates Gomery cuts allowing the search space of the
given problem. The standard Simplex Algorithm will be used to solve each Integer Linear Programming Problem (LP).
Below is an Algorithm to utilize the Branch and Cut algorithm with Gomery cuts and Partitioning:
Step 0:
Upper Bound = ∞ Lower Bound = -∞
Step 1. Initialize:
Set the first node as while setting the active nodes set as . The set can be accessed via
Step 2. Terminate:
Step 3. Iterate through list L:
While is not empty (i is the index of the list of L), then:
Step 3.1. Convert to a Relaxation:
Solve 3.2.
Solve for the Relaxed
Step 3.3.
If Z is infeasible: Return to step 3. else: Continue with solution Z.
Step 3.2. Cutting Planes:
If a cutting plane is found: then add to the linear Relaxation problem (as a constraint) and return to step 3.2 Else: Continue.
Step 4. Pruning and Fathoming:
If Z^l >= Z: return to step 3.
If Z^l <= Z AND X_i is an integral feasible: Z = Z^i Remove all Z^i from Set(L)
Step 5. Partition (reference EXTERNAL SOURCE)
Let be a partition of the constraint set of problem . Add problems to L, where is with feasible region restricted to and for j=1,...k is set to the value of for the parent problem l. Go to step 3.
Numerical Example - Chris
Application - Jon
Conclusion - Lindsay
References
https://optimization.mccormick.northwestern.edu/index.php/Branch_and_cut









