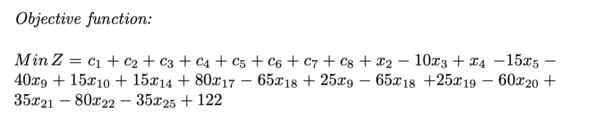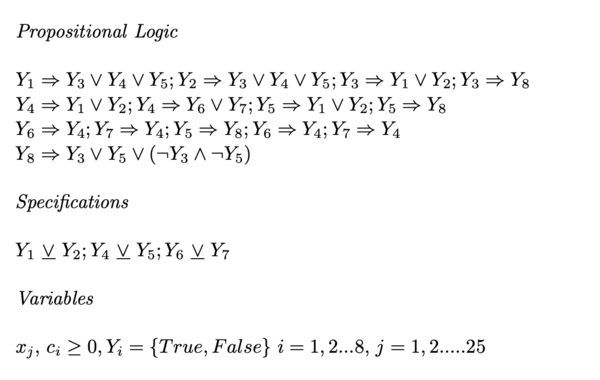Convex generalized disjunctive programming (GDP): Difference between revisions
No edit summary |
No edit summary |
||
| Line 2: | Line 2: | ||
== Introduction == | == Introduction == | ||
[ Insert picture from google doc of GDP branching to Logic Based Methods and Reformulation MI(N)LP ] | |||
== Theory == | == Theory == | ||
| Line 30: | Line 31: | ||
== Numerical Example == | == Numerical Example == | ||
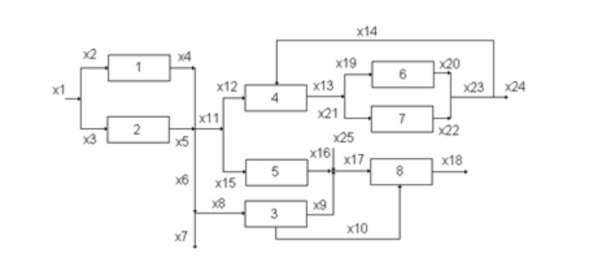
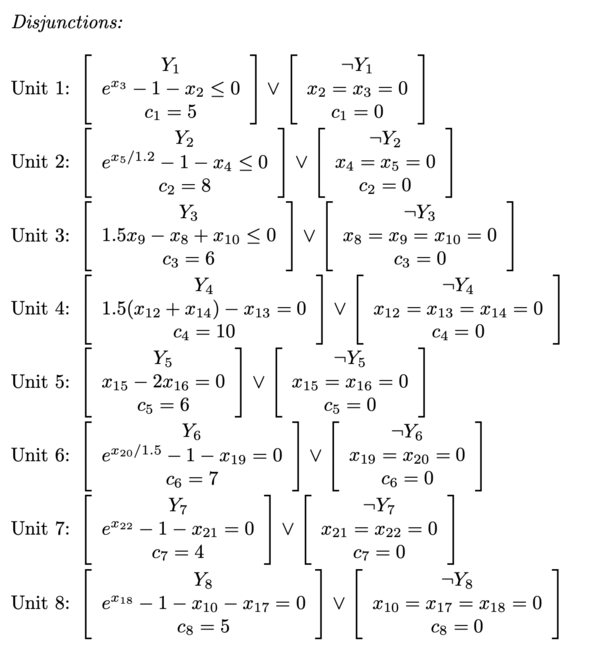
The following example was taken from: <nowiki>http://egon.cheme.cmu.edu/Papers/IMAGrossmannRuiz.pdf</nowiki> | |||
[[File:GDP numeric example 1.png|left|frameless|600x600px|Figure 1: Placeholder http://egon.cheme.cmu.edu/Papers/IMAGrossmannRuiz.pdf]] | |||
[[File:GDP numeric example 2.png|frameless|600x600px]] | |||
[[File:GDP numeric example 3.png|frameless|600x600px]] | |||
[[File:GDP numeric example 4.png|alt=http://egon.cheme.cmu.edu/Papers/IMAGrossmannRuiz.pdf|frameless|661x661px]] | |||
[[File:GDP numeric example 5.png|alt=http://egon.cheme.cmu.edu/Papers/IMAGrossmannRuiz.pdf|frameless|600x600px]] | |||
== Applications == | == Applications == | ||
Revision as of 17:39, 21 November 2020
Edited By: Nicholas Schafhauser, Blerand Qeriqi, Ryan Cuppernull
Introduction
[ Insert picture from google doc of GDP branching to Logic Based Methods and Reformulation MI(N)LP ]
Theory
Methodology
The two most common ways of reformulating a GDP problem into an MINLP are through Big-M (BM) and Hull Reformulation (HR). BM is the simpler of the two, while HR results in tighter relaxation (smaller feasible region) and faster solution times. (https://kilthub.cmu.edu/articles/A_hierarchy_of_relaxations_for_nonlinear_convex_generalized_disjunctive_programming/6466535)
Below is an example of the reformulation of the GDP problem from the Theory section reformulated into an MINLP by using the Big-M method.
Notice that the boolean term from the original GDP has been converted into a numerical {0,1}. The logic relations have also been converted into linear integer constraints (Hy).
(https://kilthub.cmu.edu/articles/journal_contribution/Improved_Big-M_Reformulation_for_Generalized_Disjunctive_Programs/6467063)
This MINLP reformulation can now be used in well-known solvers (list them here) to calculate a solution.
Numerical Example
The following example was taken from: http://egon.cheme.cmu.edu/Papers/IMAGrossmannRuiz.pdf