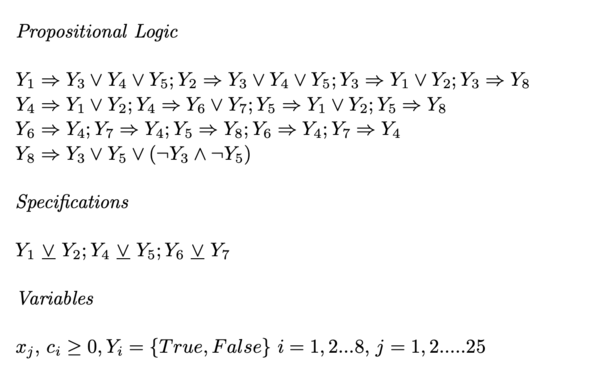Convex generalized disjunctive programming (GDP): Difference between revisions
No edit summary |
No edit summary |
||
| Line 42: | Line 42: | ||
== Applications == | == Applications == | ||
GDP formulations are useful for real-world applications where multiple branches are available when making decisions. Solving the GDP in these instances will allow the user to calculate which decisions should be made at each branching point in order to get the optimal solution. This disjunctive formulation is common in complex chemical reactions and production planning. | |||
[[File:Process network example.png|alt=http://egon.cheme.cmu.edu/Papers/IMAGrossmannRuiz.pdf|none|thumb|600x600px|Figure 1: Process Network. Each decision point represents another disjunctive set.]] | |||
The process network depicted in the figure above depicts multiple decisions that could be made to all end up at the goal (B) in a chemical reaction. This problem is able to be formulated into a GDP in order to figure out which route should be taken in order to maximize the profit. | |||
[[File:GDP numeric example 1.png|none|thumb|600x600px|Figure 2: A more complex process network.]] | |||
This same idea can be scaled to larger problems with more complex branching. Figure 2 illustrates a larger process network and all of the different decision points. This problem is able to be formulated into a GDP so that the most optimal route can be calculated to take through the network. | |||
Figures taken from: http://egon.cheme.cmu.edu/Papers/IMAGrossmannRuiz.pdf | |||
== Conclusion == | == Conclusion == | ||
== References == | == References == | ||
Revision as of 20:52, 21 November 2020
Edited By: Nicholas Schafhauser, Blerand Qeriqi, Ryan Cuppernull
Introduction
[ Insert picture from google doc of GDP branching to Logic Based Methods and Reformulation MI(N)LP ]
Theory
Methodology
The two most common ways of reformulating a GDP problem into an MINLP are through Big-M (BM) and Hull Reformulation (HR). BM is the simpler of the two, while HR results in tighter relaxation (smaller feasible region) and faster solution times. (https://kilthub.cmu.edu/articles/A_hierarchy_of_relaxations_for_nonlinear_convex_generalized_disjunctive_programming/6466535)
Below is an example of the reformulation of the GDP problem from the Theory section reformulated into an MINLP by using the Big-M method.
Notice that the boolean term from the original GDP has been converted into a numerical {0,1}. The logic relations have also been converted into linear integer constraints (Hy).
(https://kilthub.cmu.edu/articles/journal_contribution/Improved_Big-M_Reformulation_for_Generalized_Disjunctive_Programs/6467063)
This MINLP reformulation can now be used in well-known solvers (list them here) to calculate a solution.
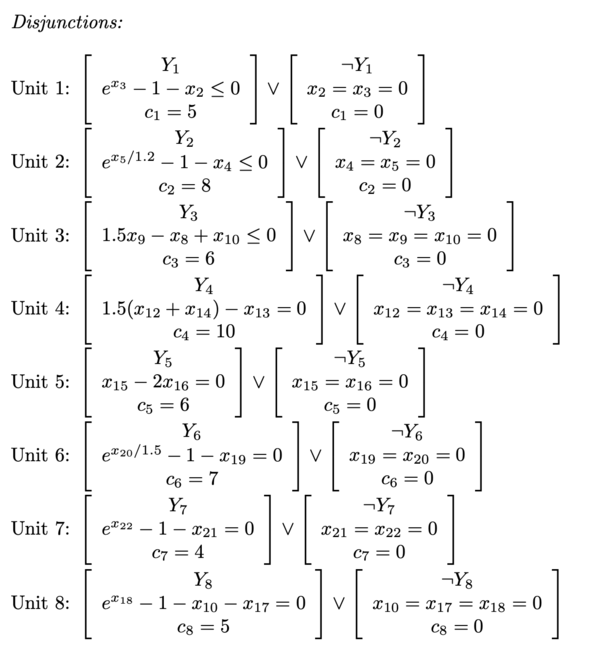
Numerical Example
The following example was taken from: http://egon.cheme.cmu.edu/Papers/IMAGrossmannRuiz.pdf
Applications
GDP formulations are useful for real-world applications where multiple branches are available when making decisions. Solving the GDP in these instances will allow the user to calculate which decisions should be made at each branching point in order to get the optimal solution. This disjunctive formulation is common in complex chemical reactions and production planning.
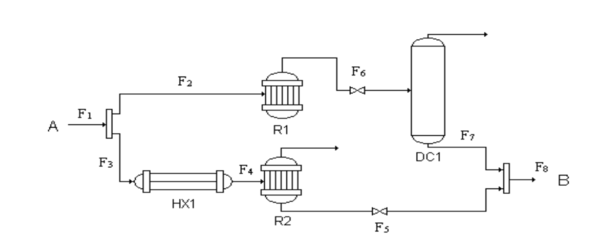
The process network depicted in the figure above depicts multiple decisions that could be made to all end up at the goal (B) in a chemical reaction. This problem is able to be formulated into a GDP in order to figure out which route should be taken in order to maximize the profit.
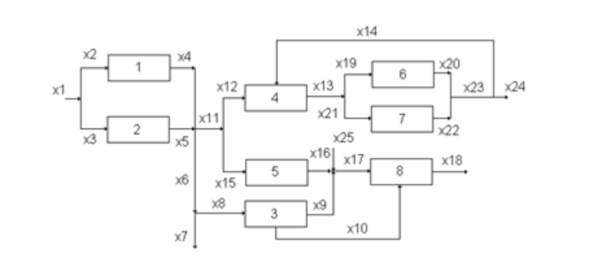
This same idea can be scaled to larger problems with more complex branching. Figure 2 illustrates a larger process network and all of the different decision points. This problem is able to be formulated into a GDP so that the most optimal route can be calculated to take through the network.
Figures taken from: http://egon.cheme.cmu.edu/Papers/IMAGrossmannRuiz.pdf