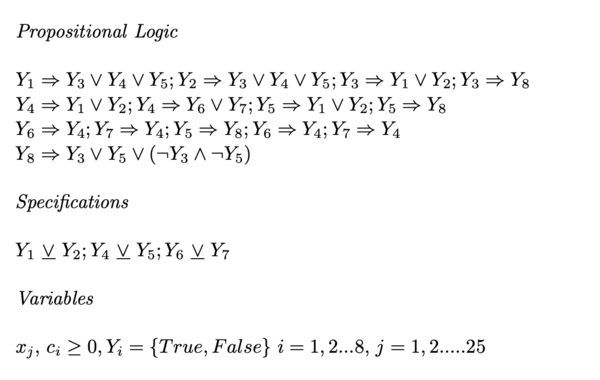Convex generalized disjunctive programming (GDP): Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
Author: Nicholas Schafhauser, Blerand Qeriqi, Ryan Cuppernull (SysEn 5800 Fall 2020) | |||
== Introduction == | == Introduction == | ||
Revision as of 07:39, 21 December 2020
Author: Nicholas Schafhauser, Blerand Qeriqi, Ryan Cuppernull (SysEn 5800 Fall 2020)
Introduction
Generalized disjunctive programming (GDP) involves logic propositions (Boolean variables) and sets of constraints that are chained together using the logical OR operator ( II ). GDP is an extension of linear disjunctive programming[1] that can be applied to Mixed Integer Non-Linear Programming (MINLP). GDP[2], is a generalization of disjunctive convex programming in the sense that it also allows the use of logic propositions that are expressed in terms of Boolean variables. In order to take advantage of current mixed-integer nonlinear programming solvers (e.g. DICOPT[3], SBB[4], α-ECP[5], BARON[6], Couenne[7] etc.), GDPs are often reformulated as MINLPs.[8]
Theory
The general form of an MINLP model is as follows
where f(x) and g(x) are twice differentiable functions, x are the continuous variables and y are the discrete variables. There are three main types of sub problems that arise from the MINLP: Continuous Relaxation, NLP subproblem for a fix and the feasibility problem.
Continuous Relaxation
The sub problem of continuous relaxation takes the form of
Where is the continuous relaxation of Y. Not that in this sub-problem all of the integer variables y are treated as continuous. This also returns a Lower Bound when it returns a feasible solution[10]
NLP Subproblem for a fixed
The subproblem for a fixed is shown in the form below
In this sub problem you return an upper bound for the MINLP program when it has a feasible solution. So with that being said you can fix a integer variables and continuously relax the others in order to get a range of feasible values.[10]
Feasibility Problem
When the fixed MINLP subproblem is not feasible the following feasibility problem is considered.
Where J is the index set for inequalities and the feasibility problem attempts to minimize the infeasibility of the solution with the most violated constraints.[10]
GDP
GDP provides a high level framework for solving the mixed non-linear integer programs. By provide a methodology for converting the disjunctive problems into a MINLP the problem becomes simplified and easier to solve using current processing and algorithmic capabilities. These methodologies that can not only solve both the Convex and Non-Convex Problems. A Convex GDP is when both f(x) and g(x) are convex functions. Which is defined as a graph where any line segment that passes through any 2 points of the plot will always be greater than the plot itself. This allows for simple relaxations/approximations to occur which will create a faster solving methodology.[11]
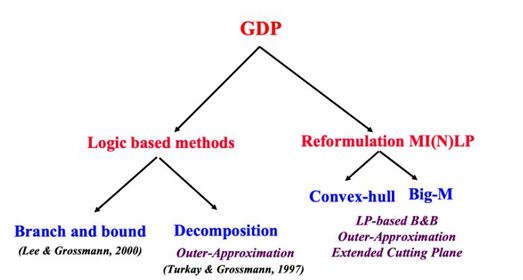
Methodology
Below is a GDP problem that will be used for demonstration purposes in this section.
The two most common ways of reformulating a GDP problem into an MINLP are through Big-M (BM) and Hull Reformulation (HR). BM is the simpler of the two, while HR results in tighter relaxation (smaller feasible region) and faster solution times.[12]
Below is an example of the the GDP problem from above reformulated into an MINLP by using the BM method.
Notice that the boolean term from the original GDP has been converted into a numerical {0,1}. The logic relations have also been converted into linear integer constraints (Hy)[8].
This MINLP reformulation can now be used in well-known solvers to calculate a solution.
The same GDP form will now be reformulated into an MINLP by using the HR method.
HR significantly increases the number of variables that are required in the same BM variant. The decrease in time needed to solve computations could very well be argued to be worth the reduced simplicity that one can get from BM.[13]
Solvers:
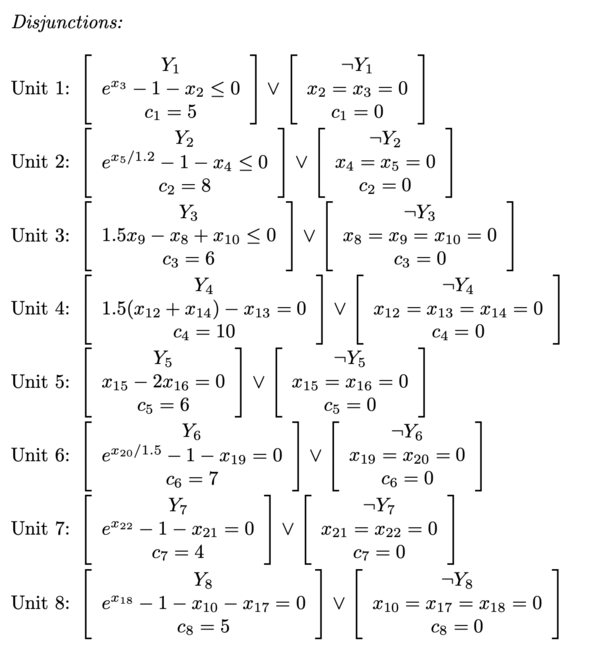
Numerical Example
The following example was taken from the paper titled Generalized Disjunctive Programming: A Framework For Formulation and Alternative Algorithms For MINLP Optimization.[14]
Applications
GDP formulations are useful for real-world applications where multiple branches are available when making decisions. Solving the GDP in these instances will allow the user to calculate which decisions should be made at each branching point in order to get the optimal solution. This disjunctive formulation is common in complex chemical reactions and production planning.
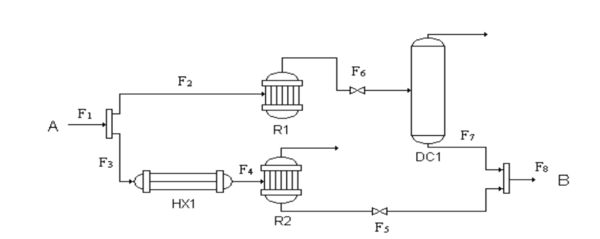
The process network depicted in the Figure 2 depicts multiple decisions that could be made to all end up at the goal (B) in a chemical reaction. This problem is able to be formulated into a GDP in order to figure out which route should be taken in order to maximize the profit.
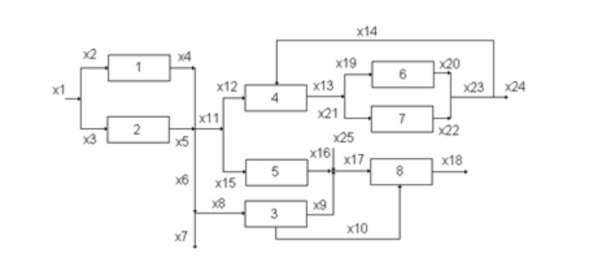
This same idea can be scaled to larger problems with more complex branching. Figure 3 illustrates a larger process network and all of the different decision points. This problem is able to be formulated into a GDP so that the most optimal route can be calculated to take through the network.
Conclusion
GDP is a programming method that applies disjunctive programming to MINLP problems. This method facilitates modeling discrete or continuous optimization problems by implementing algebraic constraints and logic expressions. The formulation of a GDP consists of Boolean and continuous variables and disjunctions and logic propositions. In the case of convex functions, GDPs can be reformulated using the BM and the HR methods. Formulation methods also include logic based methods disjunctive branch and bound and decomposition. Once reformulated into a standard MINLP, standard MILNP solvers, such as DICOPT[3], SBB[4], α-ECP[5] and BARON[6], can be used to determine optimal solutions[8]. The GDP method has important applications that include the optimization of complex chemical reactions and process planning.
References
- ↑ Balas, Egon. "Disjunctive Programming." Annals of Discrete Mathematics, 1979.
- ↑ Raman and Grossman. "Modelling and Computational Techniques for Logic Based Integer Programming." Computers & Chemical Engineering, 1994.
- ↑ 3.0 3.1 3.2 GAMS. DICOPT, https://www.gams.com/latest/docs/S_DICOPT.html
- ↑ 4.0 4.1 4.2 GAMS. SBB, 2020, www.gams.com/latest/docs/S_SBB.html.
- ↑ 5.0 5.1 GAMS. AlphaECP, 1995, https://www.gams.com/latest/docs/S_ALPHAECP.html
- ↑ 6.0 6.1 6.2 BARON, 1996, https://minlp.com/baron
- ↑ 7.0 7.1 Couenne, 2006, https://projects.coin-or.org/Couenne
- ↑ 8.0 8.1 8.2 P. Ruiz, Juan; Grossmann, Ignacio E. (2012): A hierarchy of relaxations for nonlinear convex generalized disjunctive programming. Carnegie Mellon University. Journal contribution. https://doi.org/10.1184/R1/6466535.v1
- ↑ Grossman, Ignacio E: Overview of Generalized Disjunctive Programming. Carnegie Mellon University.https://www.minlp.org/pdf/GBDEWOGrossmann.pdf
- ↑ 10.0 10.1 10.2 Grossmann, Ignacio. Review of Mixed-Integer Nonlinear and Generalized Disjunctive Programming Applications in Process Systems Engineering.
- ↑ Grossmann, Ignacio. Review of Mixed-Integer Nonlinear and Generalized Disjunctive Programming Applications in Process Systems Engineering.
- ↑ Trespalacios, Francisco; Grossmann, Ignacio E. (2018): Improved Big-M Reformulation for Generalized Disjunctive Programs. Carnegie Mellon University. Journal contribution. https://doi.org/10.1184/R1/6467063.v1
- ↑ Trespalacios, Francisco; Grossmann, Ignacio E. (2015): Algorithmic Approach for Improved Mixed-Integer Reformulations of Convex Generalized Disjunctive Programs. Carnegie Mellon University. Journal contribution. https://doi.org/10.1184/R1/6466700.v1
- ↑ 14.0 14.1 14.2 P. Ruize, Juan; Grossmann, Ignacio E.: Generalized Disjunctive Programming: A Framework For Formulation And Alternative Algorithms For MINLP Optimization. Carnegie Mellon University. http://egon.cheme.cmu.edu/Papers/IMAGrossmannRuiz.pdf