Duality: Difference between revisions
LockheedELDP (talk | contribs) |
LockheedELDP (talk | contribs) |
||
| Line 82: | Line 82: | ||
== Applications == | == Applications == | ||
Duality appears in many linear and nonlinear optimization models. One application is in Structural Design. An example of this is in a structural design model, the tension on the beams are the primal variables, and the displacements on the nodes are the dual variables. Another application for duality is when modeling electrical networks, the current flows can be modeled as the primal variables, and the voltage differences are the dual variables. In many of these applications we can solve the dual in cases when solving the primal is more difficult. If for example, there are more constraints than there are variables ''(m >> n)'', it may be easier to solve the dual. (4) | |||
Dual problems and their solutions are used in connection with the following optimization topics: | |||
* '''Karush-Kuhn-Tucker (KKT) Conditions''' | |||
The optimal solution to the dual problem is a vector of the KKT multipliers. | |||
* '''Dual Simplex Method''' | |||
Solving a Linear Programming problem by the Simplex Method gives you a solution of its dual as a by-product. زThis simplex algorithm tries to reduce the infeasibility of the dual problem. The dual simplex method can be thought of as a disguised simplex method working on the dual. The dual simplex method is when we maintain dual feasibility by imposing the condition that the objective function includes every variable with a nonpositive coefficient, and terminating when the primal feasibility conditions are satisfied. (3) | |||
== Conclusion == | == Conclusion == | ||
| Line 89: | Line 100: | ||
# https://ocw.mit.edu/courses/sloan-school-of-management/15-084j-nonlinear-programming-spring-2004/lecture-notes/lec18_duality_thy.pdf | # https://ocw.mit.edu/courses/sloan-school-of-management/15-084j-nonlinear-programming-spring-2004/lecture-notes/lec18_duality_thy.pdf | ||
# http://web.mit.edu/15.053/www/AMP-Chapter-04.pdf | # http://web.mit.edu/15.053/www/AMP-Chapter-04.pdf | ||
# http://cgm.cs.mcgill.ca/~avis/courses/567/notes/ch10.pdf | |||
# Professor You Lecture Slides (Linear Programming, Duality) | |||
Revision as of 16:31, 15 November 2020
Author: Claire Gauthier, Trent Melsheimer, Alexa Piper, Nicholas Chung, Michael Kulbacki (SysEn 6800 Fall 2020)
Steward: TA's name, Fengqi You
Introduction
Every linear programming optimization problem may be viewed either from the primal or the dual, this is the principal of duality. Duality develops the relationships between one linear programming problem and another related linear programming problem. For example in economics, if the primal optimization problem deals with production and consumption levels, then the dual of that problem relates to the prices of goods and services. The dual variables in this example can be referred to as shadow prices.
The shadow price of a constraint ...
Theory, methodology, and/or algorithmic discussions
Definition:
Primal
Maximize
subject to:
Dual
Minimize
subject to:
Between the primal and the dual, the variables and switch places with each other. The coefficient () of the primal becomes the Right Hand Side (RHS) of the dual. The RHS of the primal () becomes the coefficient of the dual. The less than or equal to constraints in the primal become greater than or equal to in the dual problem.
Constructing a Dual:
Duality Properties:
Weak Duality
- let be any feasible solution to the primal
- let be any feasible solution to the dual
- (z value for x) (v value for y)
The weak duality theorem says that the z value for x in the primal is always less than or equal to the v value of y in the dual.
Strong Duality Lemma
- let be any feasible solution to the primal
- let be any feasible solution to the dual
- if (z value for x) (v value for y), then x is optimal for the primal and y is optimal for the dual
Graphical Explanation
Essentially, as you choose values of x or y that come closer to the optimal solution, the value of z for the primal, and v for the dual will converge towards the optimal solution. On a number line, the value of z which is being maximized will approach from the left side of the optimum value while the value of v which is being minimized will approach from the right hand side.
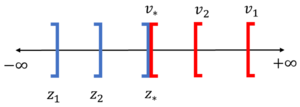
- if the primal is unbounded, then the dual is infeasible
- if the dual is unbounded, then the primal is infeasible
Numerical Example
Construct the Dual for the following maximization problem:
maximize
subject to:
For the problem above, form augmented matrix A. The first two rows represent constraints one and two respectively. The last row represents the objective function.
Find the transpose of matrix A
From the last row of the transpose of matrix A, we can derive the objective function of the dual. Each of the preceding rows represents a constraint. Note that the original maximization problem had three variables and two constraints. The dual problem has two variables and three constraints.
minimize
subject to:
Applications
Duality appears in many linear and nonlinear optimization models. One application is in Structural Design. An example of this is in a structural design model, the tension on the beams are the primal variables, and the displacements on the nodes are the dual variables. Another application for duality is when modeling electrical networks, the current flows can be modeled as the primal variables, and the voltage differences are the dual variables. In many of these applications we can solve the dual in cases when solving the primal is more difficult. If for example, there are more constraints than there are variables (m >> n), it may be easier to solve the dual. (4)
Dual problems and their solutions are used in connection with the following optimization topics:
- Karush-Kuhn-Tucker (KKT) Conditions
The optimal solution to the dual problem is a vector of the KKT multipliers.
- Dual Simplex Method
Solving a Linear Programming problem by the Simplex Method gives you a solution of its dual as a by-product. زThis simplex algorithm tries to reduce the infeasibility of the dual problem. The dual simplex method can be thought of as a disguised simplex method working on the dual. The dual simplex method is when we maintain dual feasibility by imposing the condition that the objective function includes every variable with a nonpositive coefficient, and terminating when the primal feasibility conditions are satisfied. (3)
Conclusion
References
- https://ocw.mit.edu/courses/sloan-school-of-management/15-084j-nonlinear-programming-spring-2004/lecture-notes/lec18_duality_thy.pdf
- http://web.mit.edu/15.053/www/AMP-Chapter-04.pdf
- http://cgm.cs.mcgill.ca/~avis/courses/567/notes/ch10.pdf
- Professor You Lecture Slides (Linear Programming, Duality)













![{\displaystyle x=[x_{1},...,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15924566f5cfd79ca7a295efa60abd6da45d1796)
![{\displaystyle y=[y_{1},...,y_{m}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/096997ba068d3295b74eec2e8979c33442527539)











