Duality: Difference between revisions
LockheedELDP (talk | contribs) |
m (→Duality Interpretation: Fixed typos) |
||
| (95 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
Author: Claire Gauthier, Trent Melsheimer, Alexa Piper, Nicholas Chung, Michael Kulbacki (SysEn 6800 Fall 2020) | Author: Claire Gauthier, Trent Melsheimer, Alexa Piper, Nicholas Chung, Michael Kulbacki (SysEn 6800 Fall 2020) | ||
== Introduction == | == Introduction == | ||
Every | Every optimization problem may be viewed either from the primal or the dual, this is the principle of '''duality'''. Duality develops the relationships between one optimization problem and another related optimization problem. If the primal optimization problem is a maximization problem, the dual can be used to find upper bounds on its optimal value. If the primal problem is a minimization problem, the dual can be used to find the lower bounds. | ||
According to the American mathematical scientist George Dantzig, Duality for Linear Optimization was conjectured by Jon von Neumann after Dantzig presented a problem for Linear Optimization. Von Neumann determined that two person zero sum matrix game (from Game Theory) was equivalent to Linear Programming. Proofs of the Duality theory were published by Canadian Mathematician Albert W. Tucker and his group in 1948. <ref name=":0"> Duality (Optimization). (2020, July 12). ''In Wikipedia. ''https://en.wikipedia.org/wiki/Duality_(optimization)#:~:text=In%20mathematical%20optimization%20theory%2C%20duality,the%20primal%20(minimization)%20problem.</ref> | |||
== Theory, methodology, and/or algorithmic discussions == | == Theory, methodology, and/or algorithmic discussions == | ||
=== Definition | === Definition === | ||
'''Primal'''<blockquote>Maximize <math>z=\textstyle \sum_{j=1}^n \displaystyle c_j x_j</math> </blockquote><blockquote>subject to: | '''Primal'''<blockquote>Maximize <math>z=\textstyle \sum_{j=1}^n \displaystyle c_j x_j</math> </blockquote><blockquote>subject to: | ||
<math>\textstyle \sum_{j=1}^n \displaystyle a_{i,j} x_j\lneq | </blockquote><blockquote><blockquote><math>\textstyle \sum_{j=1}^n \displaystyle a_{i,j} x_j\lneq b_i \qquad (i=1, 2, ... ,m) </math></blockquote></blockquote><blockquote><blockquote><math>x_j\gneq 0 \qquad (j=1, 2, ... ,n) </math></blockquote></blockquote><blockquote> | ||
| Line 21: | Line 18: | ||
Minimize <math>v=\textstyle \sum_{i=1}^m \displaystyle b_i y_i</math> | Minimize <math>v=\textstyle \sum_{i=1}^m \displaystyle b_i y_i</math> | ||
subject to:<blockquote><math>\textstyle \sum_{i=1}^m \displaystyle | subject to:<blockquote><math>\textstyle \sum_{i=1}^m \displaystyle y_ia_{i,j}\gneq c_j \qquad (j=1, 2, ... , n) </math></blockquote><blockquote><math>y_j\gneq 0 \qquad (i=1, 2, ... , m)</math></blockquote></blockquote>Between the primal and the dual, the variables <math>c</math> and <math>b</math> switch places with each other. The coefficient (<math>c_j</math>) of the primal becomes the right-hand side (RHS) of the dual. The RHS of the primal (<math>b_j</math>) becomes the coefficient of the dual. The less than or equal to constraints in the primal become greater than or equal to in the dual problem. <ref name=":1"> Ferguson, Thomas S. ''A Concise Introduction to Linear Programming.'' University of California Los Angeles. https://www.math.ucla.edu/~tom/LP.pdf </ref> | ||
=== Constructing a Dual === | |||
<math>\begin{matrix} \max(c^Tx) \\ \ s.t. Ax\leq b \\ x \geq 0 \end{matrix}</math> <math> \quad \longrightarrow \quad</math><math>\begin{matrix} \min(b^Ty) \\ \ s.t. A^Tx\geq c \\ y \geq 0 \end{matrix}</math> | |||
=== Duality Properties === | |||
The following duality properties hold if the primal problem is a maximization problem as considered above. This especially holds for weak duality. | |||
==== Weak Duality ==== | |||
* Let <math>x=[x_1, ... , x_n] </math> be any feasible solution to the primal | |||
* Let <math>y = [y_1, ... , y_m] </math>be any feasible solution to the dual | |||
* <math>\therefore </math>(z value for x) <math>\leq </math>(v value for y) | |||
The weak duality theorem says that the z value for x in the primal is always less than or equal to the v value of y in the dual. | |||
The difference between (v value for y) and (z value for x) is called the optimal ''duality gap'', which is always nonnegative. <ref> Bradley, Hax, and Magnanti. (1977). ''Applied Mathematical Programming.'' Addison-Wesley. http://web.mit.edu/15.053/www/AMP-Chapter-04.pdf </ref> | |||
==== Strong Duality Lemma ==== | |||
* Let <math>x=[x_1, ... , x_n] </math> be any feasible solution to the primal | |||
* Let <math>y = [y_1, ... , y_m] </math>be any feasible solution to the dual | |||
* If (z value for x) <math>= </math> (v value for y), then '''x''' is optimal for the primal and '''y''' is optimal for the dual | |||
'''Graphical Explanation''' | |||
Essentially, as you choose values of x or y that come closer to the optimal solution, the value of z for the primal, and v for the dual will converge towards the optimal solution. On a number line, the value of z which is being maximized will approach from the left side of the optimum value while the value of v which is being minimized will approach from the right-hand side. | |||
[[File:Duality numberline .png|thumb| '''Figure 1: Graphical Representation of Duality''']] | |||
* If the primal is unbounded, then the dual is infeasible | |||
* If the dual is unbounded, then the primal is infeasible | |||
==== Strong Duality Theorem ==== | |||
If the primal solution has an optimal solution <math>x^*</math> then the dual problem has an optimal solution <math>y^*</math> such that | |||
<math>\textstyle \sum_{j=1}^n \displaystyle c_j x_j^* = \textstyle \sum_{i=1}^m \displaystyle b_i y_i^*</math> | |||
Dual problems and their solutions are used in connection with the following optimization topics: | |||
'''Karush-Kuhn-Tucker (KKT) Variables''' | |||
* The optimal solution to the dual problem is a vector of the KKT multipliers. Consider we have a convex optimization problem where <math>f(x), g_1(x),...,g_m(x) </math> are convex differentiable functions. Suppose the pair <math>(\bar{x},\bar{u}) </math> is a saddlepoint of the Lagrangian and that <math>\bar{x} </math> together with <math>\bar{u} </math> satisfy the KKT conditions. The optimal solutions of this optimization problem are then <math>\bar{x} </math> and <math>\bar{u} </math> with no duality gap. <ref> ''KKT Conditions and Duality.'' (2018, February 18). Dartmouth College. https://math.dartmouth.edu/~m126w18/pdf/part4.pdf </ref> | |||
* To have strong duality as described above, you must meet the KKT conditions. | |||
* | |||
'''Dual Simplex Method''' | |||
* Solving a Linear Programming problem by the Simplex Method gives you a solution of its dual as a by-product. This simplex algorithm tries to reduce the infeasibility of the dual problem. The dual simplex method can be thought of as a disguised simplex method working on the dual. The dual simplex method is when we maintain dual feasibility by imposing the condition that the objective function includes every variable with a nonpositive coefficient, and terminating when the primal feasibility conditions are satisfied. <ref name=":3"> Chvatal, Vasek. (1977). ''The Dual Simplex Method.'' W.H. Freeman and Co. http://cgm.cs.mcgill.ca/~avis/courses/567/notes/ch10.pdf </ref> | |||
=== Duality Interpretation === | |||
* Duality can be leveraged in a multitude of interpretations. The following example includes an economic optimization problem that leverages duality: | |||
'''Economic Interpretation Example''' | |||
* A rancher is preparing for a flea market sale in which he intends to sell three types of clothing that are all comprised of wool from his sheep: peacoats, hats, and scarves. With locals socializing the high quality of his clothing, the rancher plans to sell out of all of his products each time he opens up a store at the flea market. The following shows the rancher's materials, time, and profits received for his peacoats, hats, and scarves, respectively. | |||
{| class="wikitable" | |||
|+ | |||
!Clothing | |||
!Wool (ft^2) | |||
!Sewing Material (in) | |||
!Production Time (hrs) | |||
!Profit ($) | |||
|- | |||
|Peacoat | |||
|12 | |||
|80 | |||
|7 | |||
|175 | |||
|- | |||
|Hat | |||
|2 | |||
|40 | |||
|3 | |||
|25 | |||
|- | |||
|Scarf | |||
|4 | |||
|20 | |||
|1 | |||
|21 | |||
|} | |||
* With limited materials and time for an upcoming flea market event in which the rancher will once again sell his products, the rancher needs to determine how he can make best use of his time and materials to ultimately maximize his profits. The rancher is running lower than usual on wool supply; he only has 50 square feet of wool sheets to be made for his clothing this week. Furthermore, the rancher only has 460 inches of sewing materials left. Lastly, with the rancher has a limited time of 25 hours to produce his clothing line. | |||
* | |||
* | |||
* With the above information the rancher creates the following linear program: | |||
'''maximize''' <math>z=175x_1+25x_2+21x_3</math> | |||
'''subject to:''' | |||
<math>12x_1+2x_2+4x_3\leq 50</math> | |||
<math>80x_1+40x_2+20x_3\leq 460</math> | |||
<math>7x_1+3x_2+1x_3\leq 25</math> | |||
<math>x_1,x_2,x_3\geq 0</math> | |||
* Before the rancher finds the optimal number of peacoats, hats, and scarves to produce, a local clothing store owner approaches him and asks if she can purchase his labor and materials for her store. Unsure of what is a fair purchase price to ask for these services, the clothing store owner decides to create a dual of the original primal: | |||
'''minimize''' <math>v=50y_1+460y_2+25y_3</math> | |||
'''subject to:''' | |||
<math>12y_1+80y_2+7y_3\geq 175</math> | |||
<math>2y_1+40y_2+3y_3\geq 25</math> | |||
<math>4y_1+20y_2+1y_3\geq 21</math> | |||
<math>y_1,y_2,y_3\geq 0</math> | |||
* By leveraging the above dual, the clothing store owner is able to determine the asking price for the rancher's materials and labor. In the dual, the clothing store owner's objective is now to minimize the asking price, where <math>y_1</math> represents the the amount of wool, <math>y_2</math> represents the amount of sewing material, and <math>y_3</math> represents the rancher's labor. | |||
* | |||
== Numerical Example == | == Numerical Example == | ||
=== Construct the Dual for the following maximization problem: === | |||
'''maximize''' <math>z=6x_1+14x_2+13x_3</math> | |||
'''subject to:''' | |||
<math>\tfrac{1}{2}x_1+2x_2+x_3\leq 24</math> | |||
<math>x_1+2x_2+4x_3\leq 60</math> | |||
<math>3x_1+5x_3\leq 12</math> | |||
For the problem above, form augmented matrix A. The first two rows represent constraints one and two respectively. The last row represents the objective function. | |||
<math>A =\begin{bmatrix} \tfrac{1}{2} & 2 & 1\\ 1 & 2 & 4 \\ 3 & 0 & 5 \end{bmatrix}</math> | |||
Find the transpose of matrix A | |||
<math>A^T=\begin{bmatrix} \tfrac{1}{2} & 1 & 3 \\ 2 & 2 & 0 \\ 1 & 4 & 5 \end{bmatrix}</math> | |||
From the last row of the transpose of matrix A, we can derive the objective function of the dual. Each of the preceding rows represents a constraint. Note that the original maximization problem had three variables and two constraints. The dual problem has two variables and three constraints. | |||
'''minimize''' <math>v=24y_1+60y_2+12y_3 | |||
</math> | |||
'''subject to:''' | |||
<math>\tfrac{1}{2}y_1+y_2+3y_3 \geq 6</math> | |||
<math>2y_1+2y_2\geq 14</math> | |||
<math>y_1+4y_2+5y_3\geq 13</math> | |||
== Applications == | == Applications == | ||
Duality appears in many linear and nonlinear optimization models. In many of these applications we can solve the dual in cases when solving the primal is more difficult. If for example, there are more constraints than there are variables ''(m >> n)'', it may be easier to solve the dual. A few of these applications are presented and described in more detail below. <ref name=":2"> R.J. Vanderbei. (2008). ''Linear Programming: Foundations and Extensions.'' Springer. http://link.springer.com/book/10.1007/978-0-387-74388-2. </ref> | |||
'''Economics''' | |||
* When calculating optimal product to yield the highest profit, duality can be used. For instance, the primal could be to maximize the profit, but by taking the dual the problem can be reframed into minimizing the cost. By transitioning the problem to set the raw material prices one can determine the price that the owner is willing to accept for the raw material. These dual variables are related to the values of resources available, and are often referred to as resource shadow prices. <ref> Alaouze, C.M. (1996). ''Shadow Prices in Linear Programming Problems.'' New South Wales - School of Economics. https://ideas.repec.org/p/fth/nesowa/96-18.html#:~:text=In%20linear%20programming%20problems%20the,is%20increased%20by%20one%20unit. </ref> | |||
'''Structural Design''' | |||
* An example of this is in a structural design model, the tension on the beams are the primal variables, and the displacements on the nodes are the dual variables. <ref> Freund, Robert M. (2004, February 10). ''Applied Language Duality for Constrained Optimization.'' Massachusetts Institute of Technology. https://ocw.mit.edu/courses/sloan-school-of-management/15-094j-systems-optimization-models-and-computation-sma-5223-spring-2004/lecture-notes/duality_article.pdf </ref> | |||
'''Electrical Networks''' | |||
*When modeling electrical networks the current flows can be modeled as the primal variables, and the voltage differences are the dual variables. <ref> Freund, Robert M. (2004, March). ''Duality Theory of Constrained Optimization.'' Massachusetts Institute of Technology. https://ocw.mit.edu/courses/sloan-school-of-management/15-084j-nonlinear-programming-spring-2004/lecture-notes/lec18_duality_thy.pdf </ref> | |||
'''Game Theory''' | |||
* Duality theory is closely related to game theory. Game theory is an approach used to deal with multi-person decision problems. The game is the decision-making problem, and the players are the decision-makers. Each player chooses a strategy or an action to be taken. Each player will then receive a payoff when each player has selected a strategy. The zero sum game that Von Neumann conjectured was the same as linear programming, is when the gain of one player results in the loss of another. This general situation of a zero sum game has similar characteristics to duality. <ref> Stolee, Derrick. (2013). ''Game Theory and Duality.'' University of Illinois at Urbana-Champaigna. https://faculty.math.illinois.edu/~stolee/Teaching/13-482/gametheory.pdf </ref> | |||
'''Support Vector Machines''' | |||
* Support Vector Machines (SVM) is a popular machine learning algorithm for classification. The concept of SVM can be broken down into three parts, the first two being Linear SVM and the last being Non-Linear SVM. There are many other concepts to SVM including hyperplanes, functional and geometric margins, and quadratic programming <ref> Jana, Abhisek. (2020, April). ''Support Vector Machines for Beginners - Linear SVM.'' http://www.adeveloperdiary.com/data-science/machine-learning/support-vector-machines-for-beginners-linear-svm/ </ref>. In relation to Duality, the primal problem is helpful in solving Linear SVM, but in order to get to the goal of solving Non-Linear SVM, the primal problem is not useful. This is where we need Duality to look at the dual problem to solve the Non-Linear SVM <ref> Jana, Abhisek. (2020, April 5). ''Support Vector Machines for Beginners - Duality Problem.'' https://www.adeveloperdiary.com/data-science/machine-learning/support-vector-machines-for-beginners-duality-problem/. </ref>. | |||
== Conclusion == | == Conclusion == | ||
Since proofs of Duality theory were published in 1948 <ref name=":0" /> duality has been such an important technique in solving linear and nonlinear optimization problems. This theory provides the idea that the dual of a standard maximum problem is defined to be the standard minimum problem <ref name=":1" />. This technique allows for every feasible solution for one side of the optimization problem to give a bound on the optimal objective function value for the other <ref name=":2" />. This technique can be applied to situations such as solving for economic constraints, resource allocation, game theory and bounding optimization problems. By developing an understanding of the dual of a linear program one can gain many important insights on nearly any algorithm or optimization of data. | |||
== References == | == References == | ||
Latest revision as of 10:44, 4 September 2021
Author: Claire Gauthier, Trent Melsheimer, Alexa Piper, Nicholas Chung, Michael Kulbacki (SysEn 6800 Fall 2020)
Introduction
Every optimization problem may be viewed either from the primal or the dual, this is the principle of duality. Duality develops the relationships between one optimization problem and another related optimization problem. If the primal optimization problem is a maximization problem, the dual can be used to find upper bounds on its optimal value. If the primal problem is a minimization problem, the dual can be used to find the lower bounds.
According to the American mathematical scientist George Dantzig, Duality for Linear Optimization was conjectured by Jon von Neumann after Dantzig presented a problem for Linear Optimization. Von Neumann determined that two person zero sum matrix game (from Game Theory) was equivalent to Linear Programming. Proofs of the Duality theory were published by Canadian Mathematician Albert W. Tucker and his group in 1948. [1]
Theory, methodology, and/or algorithmic discussions
Definition
Primal
Maximize
subject to:
Dual
Minimize
subject to:
Between the primal and the dual, the variables and switch places with each other. The coefficient () of the primal becomes the right-hand side (RHS) of the dual. The RHS of the primal () becomes the coefficient of the dual. The less than or equal to constraints in the primal become greater than or equal to in the dual problem. [2]
Constructing a Dual
Duality Properties
The following duality properties hold if the primal problem is a maximization problem as considered above. This especially holds for weak duality.
Weak Duality
- Let be any feasible solution to the primal
- Let be any feasible solution to the dual
- (z value for x) (v value for y)
The weak duality theorem says that the z value for x in the primal is always less than or equal to the v value of y in the dual.
The difference between (v value for y) and (z value for x) is called the optimal duality gap, which is always nonnegative. [3]
Strong Duality Lemma
- Let be any feasible solution to the primal
- Let be any feasible solution to the dual
- If (z value for x) (v value for y), then x is optimal for the primal and y is optimal for the dual
Graphical Explanation
Essentially, as you choose values of x or y that come closer to the optimal solution, the value of z for the primal, and v for the dual will converge towards the optimal solution. On a number line, the value of z which is being maximized will approach from the left side of the optimum value while the value of v which is being minimized will approach from the right-hand side.
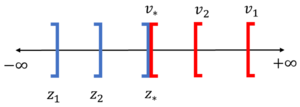
- If the primal is unbounded, then the dual is infeasible
- If the dual is unbounded, then the primal is infeasible
Strong Duality Theorem
If the primal solution has an optimal solution then the dual problem has an optimal solution such that
Dual problems and their solutions are used in connection with the following optimization topics:
Karush-Kuhn-Tucker (KKT) Variables
- The optimal solution to the dual problem is a vector of the KKT multipliers. Consider we have a convex optimization problem where are convex differentiable functions. Suppose the pair is a saddlepoint of the Lagrangian and that together with satisfy the KKT conditions. The optimal solutions of this optimization problem are then and with no duality gap. [4]
- To have strong duality as described above, you must meet the KKT conditions.
Dual Simplex Method
- Solving a Linear Programming problem by the Simplex Method gives you a solution of its dual as a by-product. This simplex algorithm tries to reduce the infeasibility of the dual problem. The dual simplex method can be thought of as a disguised simplex method working on the dual. The dual simplex method is when we maintain dual feasibility by imposing the condition that the objective function includes every variable with a nonpositive coefficient, and terminating when the primal feasibility conditions are satisfied. [5]
Duality Interpretation
- Duality can be leveraged in a multitude of interpretations. The following example includes an economic optimization problem that leverages duality:
Economic Interpretation Example
- A rancher is preparing for a flea market sale in which he intends to sell three types of clothing that are all comprised of wool from his sheep: peacoats, hats, and scarves. With locals socializing the high quality of his clothing, the rancher plans to sell out of all of his products each time he opens up a store at the flea market. The following shows the rancher's materials, time, and profits received for his peacoats, hats, and scarves, respectively.
| Clothing | Wool (ft^2) | Sewing Material (in) | Production Time (hrs) | Profit ($) |
|---|---|---|---|---|
| Peacoat | 12 | 80 | 7 | 175 |
| Hat | 2 | 40 | 3 | 25 |
| Scarf | 4 | 20 | 1 | 21 |
- With limited materials and time for an upcoming flea market event in which the rancher will once again sell his products, the rancher needs to determine how he can make best use of his time and materials to ultimately maximize his profits. The rancher is running lower than usual on wool supply; he only has 50 square feet of wool sheets to be made for his clothing this week. Furthermore, the rancher only has 460 inches of sewing materials left. Lastly, with the rancher has a limited time of 25 hours to produce his clothing line.
- With the above information the rancher creates the following linear program:
maximize
subject to:
- Before the rancher finds the optimal number of peacoats, hats, and scarves to produce, a local clothing store owner approaches him and asks if she can purchase his labor and materials for her store. Unsure of what is a fair purchase price to ask for these services, the clothing store owner decides to create a dual of the original primal:
minimize
subject to:
- By leveraging the above dual, the clothing store owner is able to determine the asking price for the rancher's materials and labor. In the dual, the clothing store owner's objective is now to minimize the asking price, where represents the the amount of wool, represents the amount of sewing material, and represents the rancher's labor.
Numerical Example
Construct the Dual for the following maximization problem:
maximize
subject to:
For the problem above, form augmented matrix A. The first two rows represent constraints one and two respectively. The last row represents the objective function.
Find the transpose of matrix A
From the last row of the transpose of matrix A, we can derive the objective function of the dual. Each of the preceding rows represents a constraint. Note that the original maximization problem had three variables and two constraints. The dual problem has two variables and three constraints.
minimize
subject to:
Applications
Duality appears in many linear and nonlinear optimization models. In many of these applications we can solve the dual in cases when solving the primal is more difficult. If for example, there are more constraints than there are variables (m >> n), it may be easier to solve the dual. A few of these applications are presented and described in more detail below. [6]
Economics
- When calculating optimal product to yield the highest profit, duality can be used. For instance, the primal could be to maximize the profit, but by taking the dual the problem can be reframed into minimizing the cost. By transitioning the problem to set the raw material prices one can determine the price that the owner is willing to accept for the raw material. These dual variables are related to the values of resources available, and are often referred to as resource shadow prices. [7]
Structural Design
- An example of this is in a structural design model, the tension on the beams are the primal variables, and the displacements on the nodes are the dual variables. [8]
Electrical Networks
- When modeling electrical networks the current flows can be modeled as the primal variables, and the voltage differences are the dual variables. [9]
Game Theory
- Duality theory is closely related to game theory. Game theory is an approach used to deal with multi-person decision problems. The game is the decision-making problem, and the players are the decision-makers. Each player chooses a strategy or an action to be taken. Each player will then receive a payoff when each player has selected a strategy. The zero sum game that Von Neumann conjectured was the same as linear programming, is when the gain of one player results in the loss of another. This general situation of a zero sum game has similar characteristics to duality. [10]
Support Vector Machines
- Support Vector Machines (SVM) is a popular machine learning algorithm for classification. The concept of SVM can be broken down into three parts, the first two being Linear SVM and the last being Non-Linear SVM. There are many other concepts to SVM including hyperplanes, functional and geometric margins, and quadratic programming [11]. In relation to Duality, the primal problem is helpful in solving Linear SVM, but in order to get to the goal of solving Non-Linear SVM, the primal problem is not useful. This is where we need Duality to look at the dual problem to solve the Non-Linear SVM [12].
Conclusion
Since proofs of Duality theory were published in 1948 [1] duality has been such an important technique in solving linear and nonlinear optimization problems. This theory provides the idea that the dual of a standard maximum problem is defined to be the standard minimum problem [2]. This technique allows for every feasible solution for one side of the optimization problem to give a bound on the optimal objective function value for the other [6]. This technique can be applied to situations such as solving for economic constraints, resource allocation, game theory and bounding optimization problems. By developing an understanding of the dual of a linear program one can gain many important insights on nearly any algorithm or optimization of data.
References
- ↑ 1.0 1.1 Duality (Optimization). (2020, July 12). In Wikipedia. https://en.wikipedia.org/wiki/Duality_(optimization)#:~:text=In%20mathematical%20optimization%20theory%2C%20duality,the%20primal%20(minimization)%20problem.
- ↑ 2.0 2.1 Ferguson, Thomas S. A Concise Introduction to Linear Programming. University of California Los Angeles. https://www.math.ucla.edu/~tom/LP.pdf
- ↑ Bradley, Hax, and Magnanti. (1977). Applied Mathematical Programming. Addison-Wesley. http://web.mit.edu/15.053/www/AMP-Chapter-04.pdf
- ↑ KKT Conditions and Duality. (2018, February 18). Dartmouth College. https://math.dartmouth.edu/~m126w18/pdf/part4.pdf
- ↑ Chvatal, Vasek. (1977). The Dual Simplex Method. W.H. Freeman and Co. http://cgm.cs.mcgill.ca/~avis/courses/567/notes/ch10.pdf
- ↑ 6.0 6.1 R.J. Vanderbei. (2008). Linear Programming: Foundations and Extensions. Springer. http://link.springer.com/book/10.1007/978-0-387-74388-2.
- ↑ Alaouze, C.M. (1996). Shadow Prices in Linear Programming Problems. New South Wales - School of Economics. https://ideas.repec.org/p/fth/nesowa/96-18.html#:~:text=In%20linear%20programming%20problems%20the,is%20increased%20by%20one%20unit.
- ↑ Freund, Robert M. (2004, February 10). Applied Language Duality for Constrained Optimization. Massachusetts Institute of Technology. https://ocw.mit.edu/courses/sloan-school-of-management/15-094j-systems-optimization-models-and-computation-sma-5223-spring-2004/lecture-notes/duality_article.pdf
- ↑ Freund, Robert M. (2004, March). Duality Theory of Constrained Optimization. Massachusetts Institute of Technology. https://ocw.mit.edu/courses/sloan-school-of-management/15-084j-nonlinear-programming-spring-2004/lecture-notes/lec18_duality_thy.pdf
- ↑ Stolee, Derrick. (2013). Game Theory and Duality. University of Illinois at Urbana-Champaigna. https://faculty.math.illinois.edu/~stolee/Teaching/13-482/gametheory.pdf
- ↑ Jana, Abhisek. (2020, April). Support Vector Machines for Beginners - Linear SVM. http://www.adeveloperdiary.com/data-science/machine-learning/support-vector-machines-for-beginners-linear-svm/
- ↑ Jana, Abhisek. (2020, April 5). Support Vector Machines for Beginners - Duality Problem. https://www.adeveloperdiary.com/data-science/machine-learning/support-vector-machines-for-beginners-duality-problem/.













![{\displaystyle x=[x_{1},...,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15924566f5cfd79ca7a295efa60abd6da45d1796)
![{\displaystyle y=[y_{1},...,y_{m}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/096997ba068d3295b74eec2e8979c33442527539)
































