Dynamic optimization: Difference between revisions
(Created page with " Authors: Hanyu Shi (ChE 345 Spring 2014) Steward: Dajun Yue, Fengqi You Date Presented: Apr. 10, 2014 Authors: Issac Newton, Albert Einstein (ChE 345 Spring 2014) Stewar...") |
No edit summary |
||
| Line 1: | Line 1: | ||
This web page is a duplicate of https://optimization.mccormick.northwestern.edu/index.php/Dynamic_optimization | |||
Authors: Hanyu Shi (ChE 345 Spring 2014) | Authors: Hanyu Shi (ChE 345 Spring 2014) | ||
Revision as of 11:35, 1 April 2022
This web page is a duplicate of https://optimization.mccormick.northwestern.edu/index.php/Dynamic_optimization Authors: Hanyu Shi (ChE 345 Spring 2014)
Steward: Dajun Yue, Fengqi You
Date Presented: Apr. 10, 2014
Authors: Issac Newton, Albert Einstein (ChE 345 Spring 2014)
Steward: Dajun Yue, Fengqi You
Date Presented: Apr. 10, 2014
Introduction
In this work, we will focus on the “at the same time” or direct transcription approach which allow a simultaneous method for the dynamic optimization problem. In particular, we formulate the dynamic optimization model with orthogonal collocation methods. These methods can also be regarded as a special class of implicit Runge–Kutta (IRK) methods. We apply the concepts and properties of IRK methods to the differential equations directly. With locating potential break points appropriately, this approach can model large-scale optimization formulations with the property of maintaining accurate state and control profiles. We mainly follows Biegler's work.
General Dynamic Optimization Problem
Differential algebraic equations in process engineering often have following characteristics: first,large-scale models – not easily scaled; second, sparse but no regular structure; third, direct linear solvers widely used; last, coarse-grained decomposition of linear algebra.
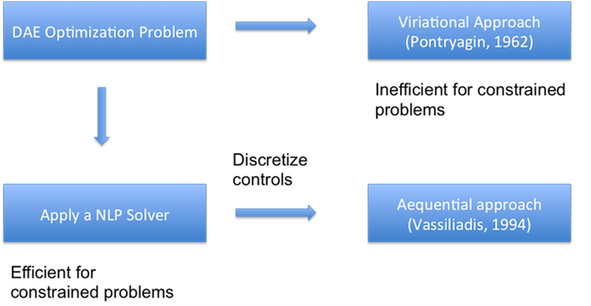
Figure 2. Dynamic optimization approach
There are several approaches can be applied to solve the dynamic optimization problems, which are shown in Figure 2.
Differential equations can usually be used to express conservation Laws, such as mass, energy, momentum. Algebraic equations can usually be used to express constitutive equations, equilibrium, such as physical properties, hydraulics, rate laws. Algebraic equations usually have semi-explicit form and assume to be index one i.e., algebraic variables can be solved uniquely by algebraic equations.
Dynamic Optimization Problem has the following general form:
, time
, differential variables y, algebraic variables
, final time
, control variables
, time independent parameters
(This follows Biegler's slides )
Derivation of Collocation Methods
We first consider the differential algebraic system shown as follows:
(1)
The simultaneous approach requires discretizing of the state variables , output variables and manipulate variables . We require the following properties to yield an efficient NLP formulation:
1) The explicit ODE discretization holds little computational advantage because Since the nonlinear program requires an iterative solution of the KKT conditions.
2) A single step approach which is self-starting and does not rely on smooth profiles that extend over previous time steps is preferred, because the NLP formulation needs to deal with discontinuities in control profiles.
3) The high-order implicit discretization provides accurate profiles with relatively few finite elements. As a result, the number of finite elements need not be excessively large, particularly for problems with many states and controls.
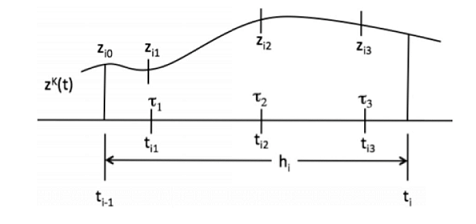
Figure 1: Polynomial approximation for state profile across a finite element.
Polynomial Representation for ODE Solutions
We consider the following ODE:
(2)
to apply the collocation method, we need to solve the differential equation (2) at certain points. For the state variable, we consider a polynomial approximation of order (i.e., degree ≤ ) over a single finite element, as shown in the above figure. This polynomial, denoted by , can be represented in a number of equivalent ways, including the power series representation shown in equation (3), the Newton divided difference approximation, or B-splines.
(3)
We apply representations based on Lagrange interpolation polynomials to generate the NLP formulation, because the polynomial coefficients and the profiles have the same variable bounds. Here we select interpolation points in element i and represent the state in a given element as
(4)
, and hi is the length of element . This polynomial representation has the desirable property that , where .
We use a Lagrange polynomial with K interpolation points to represent the time derivative of the state. This leads to the Runge–Kutta basis representation for the differential state:
(5)
where is a coefficient that represents the differential state at the beginning of element , represents the time derivative , and is a polynomial of order K satisfying
(6)
We substitute the polynomial into equation (1) to calculate the polynomial coefficients, which is an approximation of the DAE. This results in the following collocation equations.
(7)
with calculated separately. For the polynomial representations (4) and (5), we normalize time over the element, write the state profile as a function of τ , and apply easily. For the Lagrange polynomial (4), the collocation equations become
(8)
while the collocation equations for the Runge–Kutta basis are given by
(9)
(10)
with determined from the previous element or from the initial condition on the ODE.
Example
An example is given here to demonstrate the application of the collocation method.
A differential equation is given as follows:
(11)
With t \in \left[ {0,1} \right], The analytic solution of this differential equation is .
Lagrange interpolation and collocation method is applied to this differential equation respectively. And the number of collocation points in each finite element is 3. The number of finite elements is N , and the length of the finite element is 1/N . The following equations is given then:
(12)
(13)
(14)
With Radau collocation method, , , and can be obtained. The collocation equations are given as follows:
(14)
which can be formulated as:
(15)
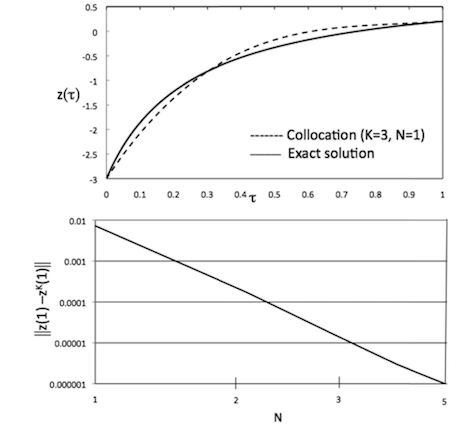
Figure 3. Comparison of Radau collocation solution with exact solution
The results are given as following by solving the above equations:
(16)
As shown in Figure 3.2 the error , is less than for and converges with , which is consistent with the expected order .
(This example follows the work of Biegler and can be found in P293 of “ Nonlinear Programmng”.)
Conclusion
In this work, we mainly discussed simultaneous collocation approach for dynamic optimization problems, which formulated the differential equations to a set of algebraic equations. These direct transcription formulations depended on fully discretizing of the differential algebraic equations (DAE), which enabled us solve the simultaneous optimization problem without relying on embedded DAE solvers. Because of this simultaneous formulation, we got the exact first and second order derivatives through the optimization modeling system, and both structure and sparsity can be exploited.
References
1. Biegler, Lorenz T. Nonlinear programming: concepts, algorithms, and applications to chemical processes. Vol. 10. SIAM, 2010.
2. Chu, Yunfei, and Fengqi You. "Integration of scheduling and control with online closed-loop implementation: Fast computational strategy and large-scale global optimization algorithm." Computers & Chemical Engineering 47 (2012): 248-268.
3. http://en.wikipedia.org/wiki/Dynamic_programming
4. http://en.wikipedia.org/wiki/Differential_algebraic_equation















![{\displaystyle {\begin{array}{l}\left.{\begin{array}{*{20}{c}}{t={t_{i-1}}+{h_{i}}\cdot \tau ,}\\{{z^{K}}\left(t\right)=\sum \limits _{j=0}^{K}{{l_{j}}\left(\tau \right)\cdot {z_{ij}},}}\end{array}}\right\}t\in \left[{{t_{i-1}},{t_{i}}}\right],\tau \in \left[{0,1}\right],\\where\;{l_{j}}\left(\tau \right)=\prod \limits _{k=0,\neq j}^{K}{\frac {\left({\tau -{\tau _{k}}}\right)}{\left({{\tau _{j}}-{\tau _{k}}}\right)}},\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d55e364011517b657e50d9bc2948823a07084573)








![{\displaystyle {\Omega _{j}}\left(\tau \right)=\int _{0}^{\tau }{{l_{j}}(\tau ')}d\tau ',t\in \left[{{t_{i-1}},{t_{i}}}\right],\tau \in \left[{0,1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6aae91362aea8b6ddeb90342f0fa7b0929d32dd)