Facility location problem: Difference between revisions
Lawrenceli (talk | contribs) No edit summary |
No edit summary |
||
| Line 37: | Line 37: | ||
== Numerical Example == | == Numerical Example == | ||
Suppose a paper products manufacturer has enough capital to build and manage an additional manufacturing plant in the United States in order to meet increased demand in three cities: New York City, NY, Los Angeles, CA, and Topeka, KS. The company already has distribution facilities in Denver, CO, Seattle, WA, and St. Louis, MO, and due to limited capital, cannot build an additional distribution facility. So, they must choose to build their new plant in one of these three locations. Due to geographic constraints, plants in Denver, Seattle, and St. Louis would have a maximum operating capacity of 400tons/day, 700 tons/day, and 600 tons/day, respectively. The cost of transporting the products from the plant to the city is directly proportional, and an outline of the supply, demand, and cost of transportation is shown in the figure below. | |||
[[File:Example.png|center|780x780px]] | |||
To solve this problem, we will assign the following variables: | |||
<math>i</math> is the factory location | |||
<math>j</math> is the factory location | |||
<math>C_{ij}</math> | |||
== Applications == | == Applications == | ||
Revision as of 18:36, 17 November 2020
Authors: Liz Cantlebary, Lawrence Li (CHEME 6800 Fall 2020)
Stewards: Allen Yang, Fengqi You
Introduction
The Facility Location Problem (FLP) is a classic optimization problem that determines the best location for a factory or warehouse to be placed based on geographical demands, facility costs, and transportation distances. These problems generally aim to maximize the supplier's profit based on the given customer demand and location. FLP can be further broken down into capacitated and uncapacitated problems, depending on whether the facilities in question have a maximum capacity or not.
Theory and Formulation
Weber Problem
The Weber Problem is a simple FLP that consists of locating the geometric median between three points with different weights. The geometric median is a point between three given points in space such that the sum of the distances between the median and the other three points is minimized. It is based on the premise of minimizing transportation costs from one point to various destinations, where each destination has a different associated cost per unit distance.
Given points on a plane with associated weights , the 2-dimensional Weber problem to find the geometric median is formulated as(1)
where
Capacitated and Uncapacitated FLPs
A capacitated facility problem applies constraints to the production and transportation capacity of each facility. As a result, customers may not be supplied by the most immediate facility, since this facility may not be able to satisfy the given customer demand.
In a problem with facilities and customers, the capacitated formulation defines a binary variable and a variable for each facility and each customer . If facility is open, ; otherwise . Open facilities have an associated fixed cost and a maximum capacity . is the fraction of the total demand of customer that facility has satisfied and the transportation cost between facility and customer is represented as . The capacitated FLP is therefore defined as
In an uncapacitated facility problem, the amount of product each facility can produce and transport is assumed to be unlimited, and the optimal solution results in customers being supplied by the lowest-cost, and usually the nearest, facility. Using the above formulation, the unlimited capacity means can be assumed to be a sufficiently large constant, while is now a binary variable, because the demand of each customer can be fully met with the nearest facility. If facility supplies customer , then ; otherwise .
Numerical Example
Suppose a paper products manufacturer has enough capital to build and manage an additional manufacturing plant in the United States in order to meet increased demand in three cities: New York City, NY, Los Angeles, CA, and Topeka, KS. The company already has distribution facilities in Denver, CO, Seattle, WA, and St. Louis, MO, and due to limited capital, cannot build an additional distribution facility. So, they must choose to build their new plant in one of these three locations. Due to geographic constraints, plants in Denver, Seattle, and St. Louis would have a maximum operating capacity of 400tons/day, 700 tons/day, and 600 tons/day, respectively. The cost of transporting the products from the plant to the city is directly proportional, and an outline of the supply, demand, and cost of transportation is shown in the figure below.
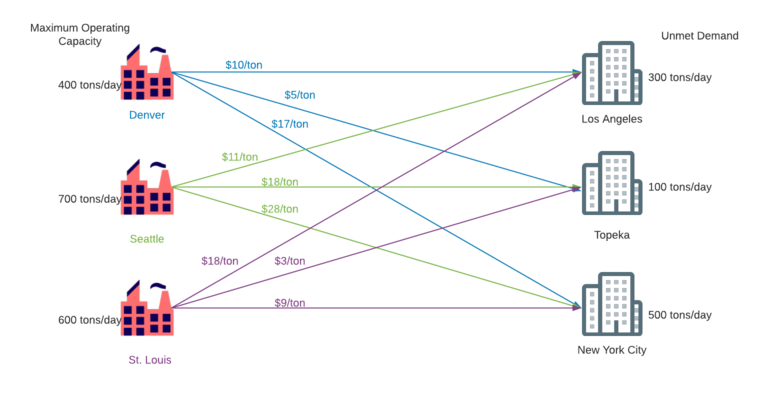
To solve this problem, we will assign the following variables: is the factory location
is the factory location
Applications
Conclusion
References
- http://www.pitt.edu/~lol11/ie1079/notes/ie2079-weber-slides.pdf
- Drezner, Z; Hamacher. H. W. (2004), Facility Location Applications and Theory. New York, NY: Springer.
- Eiselt, H.A.; Marianov, V. (2019), Contributions to Location Analysis. Cham, Switzerland: Springer.





















