Facility location problem: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
Authors: Liz Cantlebary, Lawrence Li ( | Authors: Liz Cantlebary, Lawrence Li (ChemE 6800 Fall 2020) | ||
== Introduction == | == Introduction == | ||
Latest revision as of 07:35, 21 December 2020
Authors: Liz Cantlebary, Lawrence Li (ChemE 6800 Fall 2020)
Introduction
The Facility Location Problem (FLP) is a classic optimization problem that determines the best location for a factory or warehouse to be placed based on geographical demands, facility costs, and transportation distances. These problems generally aim to maximize the supplier's profit based on the given customer demand and location(1). FLP can be further broken down into capacitated and uncapacitated problems, depending on whether the facilities in question have a maximum capacity or not(2).
Theory and Formulation
Weber Problem and Single Facility FLPs
The Weber Problem is a simple FLP that consists of locating the geometric median between three points with different weights. The geometric median is a point between three given points in space such that the sum of the distances between the median and the other three points is minimized. It is based on the premise of minimizing transportation costs from one point to various destinations, where each destination has a different associated cost per unit distance.
Given points on a plane with associated weights , the 2-dimensional Weber problem to find the geometric median is formulated as(1)
where
The above formulation serves as a foundation for many basic single facility FLPs. For example, the minisum problem aims to locate a facility at the point that minimizes the sum of the weighted distances to the given set of existing facilities, while the minimax problem consists of placing the facility at the point that minimizes the maximum weighted distance to the existing facilities(3). Additionally, in contrast to the minimax problem, the maximin facility problem maximizes the minimum weighted distance to the given facilities.
Capacitated and Uncapacitated FLPs
FLPs can often be formulated as mixed-integer programs (MIPs), with a fixed set of facility and customer locations. Binary variables are used in these problems to represent whether a certain facility is open or closed and whether that facility can supply a certain customer. Capacitated and uncapacitated FLPs can be solved this way by defining them as integer programs.
A capacitated facility problem applies constraints to the production and transportation capacity of each facility. As a result, customers may not be supplied by the most immediate facility, since this facility may not be able to satisfy the given customer demand.
In a problem with facilities and customers, the capacitated formulation defines a binary variable and a variable for each facility and each customer . If facility is open, ; otherwise . Open facilities have an associated fixed cost and a maximum capacity . is the fraction of the total demand of customer that facility has satisfied and the transportation cost between facility and customer is represented as . The capacitated FLP is therefore defined as(2)
In an uncapacitated facility problem, the amount of product each facility can produce and transport is assumed to be unlimited, and the optimal solution results in customers being supplied by the lowest-cost, and usually the nearest, facility. Using the above formulation, the unlimited capacity means can be assumed to be a sufficiently large constant, while is now a binary variable, because the demand of each customer can be fully met with the nearest facility(2). If facility supplies customer , then ; otherwise .
Approximate and Exact Algorithms
A variety of approximate algorithms can be used to solve facility location problems. These algorithms terminate after a given number of steps based on the size of the problem, yielding a feasible solution with an error that does not exceed a constant approximation ratio(4). This ratio indicates that the approximate solution is no greater than the exact solution by a factor of .
While greedy algorithms generally do not perform well on FLPs, the primal-dual greedy algorithm presented by Jain and Vazirani tends to be faster in solving the uncapacitated FLP than LP-rounding algorithms, which solve the LP relaxation of the integer formulation and round the fractional results(4). The Jain-Vazirani algorithm computes the primal and the dual to the LP relaxation simultaneously and guarantees a constant approximation ratio of 1.861(5). This solver has a running time complexity of , where corresponds to the number of edges between facilities and cities. Improving upon this primal-dual approach, the modified Jain-Mahdian-Saberi algorithm guarantees a better approximation ratio for the uncapacitated problem(5).
To solve the capacitated FLP, which often contains more complex constraints, many algorithms utilize a Lagrangian decomposition(6), first introduced by Held and Karp in the traveling salesman problem(7). This approach allows constraints to be relaxed by penalizing this relaxation while solving a simplified problem. The capacitated problem has been effectively solved using this Lagrangian relaxation in conjunction with the volume algorithm, which is a variation of subgradient optimization presented by Barahona and Anbil(8).
Exact methods have also been presented for solving FLPs. To solve the -median capacitated facility location problem, Ceselli introduces a branch-and-bound method that solves a Lagrangian relaxation with subgradient optimization, as well as a separate branch-and-price algorithm that utilizes column generation(9). Ceselli's work indicates that branch-and-bound works well when the ratio of sites to customers is low, but the performance and run-time worsen significantly as this ratio increases. In comparison, the branch-and-price method demonstrates much more stable performance across various problem sizes and is generally faster overall.
Numerical Example
Suppose a paper products manufacturer has enough capital to build and manage an additional manufacturing plant in the United States in order to meet increased demand in three cities: New York City, NY, Los Angeles, CA, and Topeka, KS. The company already has distribution facilities in Denver, CO, Seattle, WA, and St. Louis, MO, and due to limited capital, cannot build an additional distribution facility. So, they must choose to build their new plant in one of these three locations. Due to geographic constraints, plants in Denver, Seattle, and St. Louis would have a maximum operating capacity of 400 tons/day, 700 tons/day, and 600 tons/day, respectively. The cost of transporting the products from the plant to the city is directly proportional, and an outline of the supply, demand, and cost of transportation is shown in the figure below. Regardless of where the plant is built, the selling price of the product is $100/ton.
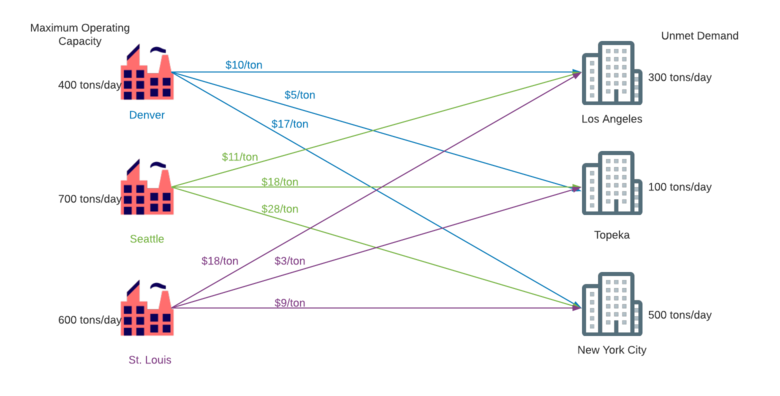
Exact Solution
To solve this problem, we will assign the following variables:
is the factory location
is the city destination
is the cost of transporting one ton of product from the factory to the city
is the amount of product transported from the factory to the city in tons
is the maximum operating capacity at the factory
is the amount of unmet demand in the city
To determine where the company should build the factory, we will carry out the following optimization problem for each location to maximize the profit from each ton sold:
max
subject to
The problem is solved in GAMS (General Algebraic Modeling System).
If the factory is built in Denver, 300 tons/day of product go to Los Angeles and 100 tons/day go to Topeka, for a total profit of $36,300/day.
If the factory is built in Seattle, 300 tons/day of product go to Los Angela, 100 tons/day of product go to Topeka, and 300 tons/day go to New York City, for a total profit of $56,500/day.
If the factory is built in St. Louis, 100 tons/day of product go to Topeka and 500 tons/day go to New York City, for a total profit of $55,200/day.
Therefore, to maximize profit, the factory should be built in Seattle.
Approximate Solution
This example can also be solved approximately through the branch and bound method. The tree diagram showing the optimization is shown below.
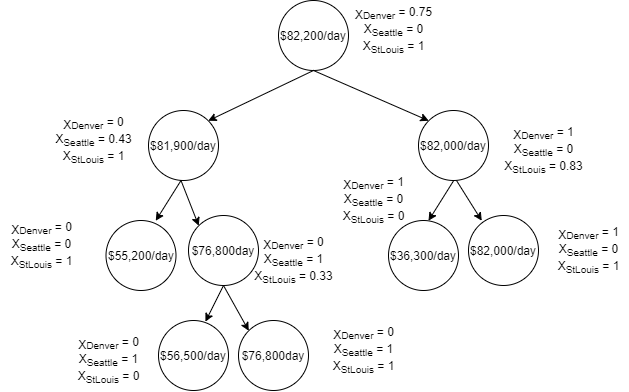
As shown in the tree diagram, building factories in both Denver and St. Louis would yield the highest profit of $82,200/day. Unfortunately, the company only has enough capital to build one facility. As a result of this, the only acceptable values are those in which one value is "1" and two are "0". Based on this constraint, it is clear that the company should build the factory in Seattle, as shown in the exact solution above. However, this also yields valuable information if the company hopes to expand again in the near future, because building a factories in St. Louis and Denver is more profitable than building factories in Seattle and Denver or Seattle and St. Louis. Depending on company projections, it may be a better decision to build the first factory St. Louis and aim to build an additional factory in Denver as soon as possible.
Applications
Facility location problems are utilized in many industries to find the optimal placement of various facilities, including warehouses, power plants, public transportation terminals, polling locations, and cell towers, to maximize efficiency, impact, and profit. In more unique applications, extensive research has been done in applying FLPs to humanitarian efforts, such as identifying disaster management sites to maximize accessibility to healthcare and treatment(10). A case study by researchers in Nigeria explored the application of mixed-integer FLPs in optimizing the locations of waste collection centers to provide sanitation services in crucial communities. More effective waste collection systems could combat unsanitary practices and environmental pollution, which are major concerns in many developing nations(11). For example, Badran and El-Haggar proposed a solid waste management system for Port Said, Egypt, implementing a mixed-integer program to optimally place waste collection stations and minimize cost(12). This program was formulated to select collection stations from a set of locations such that the sum of the fixed cost of opening collections stations, the operating costs of the collection stations, and the transportation costs from the collection stations to the composting plants is minimized.
FLPs have also been used in clustering analysis, which involves partitioning a given set of elements (e.g. data points) into different groups based on the similarity of the elements. The elements can be placed into groups by identifying the locations of center points that effectively partition the set into clusters, based on the distances from the center points to each element(13). For example, the -median clustering problem can be formulated as a FLP that selects a set of cluster centers to minimize the cost between each point and its closest center. The cost in this problem is represented as the Euclidean distance between a point and a proposed cluster center . The problem can be formulated as the following integer program, which selects centers from a set of points(13).
In this formulation, the binary variables and represent whether is used as a center point and whether is the optimal center for , respectively. The -median problem is NP-hard and is commonly solved using approximation algorithms. One of the most effective algorithms to date, proposed by Byrka et al., has an approximation factor of 2.611(13).
Conclusion
The facility location problem is an important application of computational optimization. The uses of this optimization technique are far-reaching, and can be used to determine anything from where a family should live based on the location of their workplaces and school to where a Fortune 500 company should put a new manufacturing plant or distribution facility to maximize their return on investment.
References
- Drezner, Z; Hamacher. H. W. (2004), Facility Location Applications and Theory. New York, NY: Springer.
- Francis, R. L.; Mirchandani, P. B. (1990), Discrete Location Theory. New York, NY: Wiley.
- Hansen, P., et al. (1985), The Minisum and Minimax Location Problems Revisited. Operations Research, 33, 6, 1251-1265.
- Vygen, J. (2005), Approximation Algorithms for Facility Location Problems. Research Institute for Discrete Mathematics, University of Bonn.
- Jain, K., et al. (2003), A Greedy Facility Location Algorithm Analyzed Using Dual Fitting with Factor-Revealing LP. Journal of the ACM, 50, 6, 795-824.
- Alenezy, E. J. (2020), Solving Capacitated Facility Location Problem Using Lagrangian Decomposition and Volume Algorithm. Advances in Operations Research, 2020, 5239176, 2020.
- Held, M.; Karp, R. M. (1970), The Traveling-Salesman Problem and Minimum Spanning Trees. Operations Research, 18, 6, 1138-1162.
- Barahona, F.; Anbil, R. (2000), The Volume Algorithm: Producing Primal solutions with a Subgradient Method. Mathematical Programming, 87, 3, 385–399.
- Ceselli, A. (2003), Two Exact Algorithms for the Capacitated p-Median Problem. Quarterly Journal of the Belgian, French and Italian Operations Research Societies, 4, 1, 319-340.
- Daskin, M. S.; Dean, L. K. (2004), Location of Health Care Facilities. Handbook of OR/MS in Health Care: A Handbook of Methods and Applications, 43-76.
- Adeleke, O. J.; Olukanni, D. O. (2020), Facility Location Problems: Models, Techniques, and Applications in Waste Management. Recycling, 5, 10.
- Badran, M.F.; El-Haggar, S.M. (2006), Optimization of Municipal Solid Waste Management in Port Said – Egypt. Waste Management, 26, 5, 534-545.
- Meira, L. A. A., et al. (2017), Clustering through Continuous Facility Location Problems. Theoretical Computer Science, 657, 137-145.
- Balcik, B.; Beamon, B. M. (2008), Facility Location in Humanitarian Relief. International Journal of Logistics Research and Applications, 11, 101-121.
- Eiselt, H. A.; Marianov, V. (2019), Contributions to Location Analysis. Cham, Switzerland: Springer.














































