Fuzzy programming

Authors: Kyle Clark, Matt Schweider, Tommy Sheehan, Jared Melancon (SYSEN 6800, Fall 2020)

Steward: Wei-Han Chen, Fengqi You

Introduction

Fuzzy Programming is an optimization model that deals with performing optimization in the presence of uncertainty. This optimization technique is used when determining the exactness of a system's performance criteria/parameters and decision variables is not possible. Specifically, the truth values associated with the system can be completely false (0), completely true (1), or some value between the two extremes. This aims to capture the concept of partial truth. One approach to account for uncertainty in a system is to model the uncertainty using probability distributions, also know as statistical analysis. However, sometimes uncertainty is sometimes described using qualitative adjectives, or 'Fuzzy' statements, such as young or old, and hot or cold, because exact boundaries do not necessarily exist [1].

Fuzzy Programming is built on the concept of Fuzzy Logic. The motivation for Fuzzy Logic, or more precisely Fuzzy Set Theory, is to accurately model and represent real world data which is often 'Fuzzy' due to uncertainty. This uncertainty can be introduced into a system by a number of factors such as imprecision in measurement tools or due to the use of vague language [2].

Fuzzy Logic

While Boolean Logic is used to describe situations as completely true or completely false, Fuzzy Logic allows for a mathematical representation of partial truth or partial falsehood. Rather than having strict criteria for defining what is part of the set and what is not (e.g. hot or cold, young or old), we allow data to have a degree of membership (u) to each set. A membership function defines how each input value is mapped to a degree of membership (u) between the two extremes, 0 and 1. Membership functions can be several different types of functions. However, they are often Piece-Wise Linear Functions [3]. Below in an example of an L-Function.

$u_{A}(x)={\begin{cases}0,\qquad x\leq b\\{\frac {x-a}{b-a}},\quad a\leq x\leq b\\1,\qquad x>b\end{cases}}$

For instance, let's say that we have a set of values that describe temperatures over the course of a week. In Boolean logic, we could create two sets, a cold set and an hot set. We could say that temperatures [0°F, 60°F) belong to the cold set and temperatures [60°F, 100°F] belong to the hot set. However, it is not very accurate to say that 60°F is cold, but 60.1°F is hot. Instead, we could use Fuzzy Logic to describe temperatures 0°F - 50°F as not hot (u=0). As temperatures increase from 50°F, they are given a higher degree of membership (u>0) to describe that they are "more hot" or warm. Lastly, temperatures above 70°F are definitely hot (u=1) [3].

Flexible Mathematical Programming Method

An optimization technique used to implement Fuzzy Programming is Flexible Mathematical Programming. This kind of problem takes on the form of

${\begin{cases}{\tilde {min}}f(x)\\s.t.\ g_{i}(x)\leq \sim b_{i};i=1,...,m\\x\in X=\{x\in \mathbb {R} ^{2}|x\geq 0\}\end{cases}}$

where the "~" conveys the concept that the objective statement and constraints have some freedom in how they are satisfied. This approach is useful when strict satisfaction of the constraints creates an empty feasible set. Relaxing the constraints with the "~" allows for maneuverability within the potential solutions.

An easier way to represent the constraints is through the use of membership functions which are fuzzy sets of $\mathbb {R}$.

$u_{i}(x)=0\qquad \ \ \ if\ g_{i}(x)>b_{i}+d_{i}$

$u_{i}(x)\in (0,1)\quad if\ b_{i}<g_{i}(x)\leq b_{i}+d_{i}$

$u_{i}(x)=1\qquad \ \ if\ g_{i}(x)\leq b_{i}$

where $d_{i}(i=1,...,m)$ represents the set of constraints which have a certain threshold that can be violated. The above membership functions are used to determine the degree of membership or how violated a certain constraint is. If $u_{i}(x)=1$, then the constraint is not violation. If $u_{i}(x)=0$, then the constraint is violated. The in between case of $u_{i}(x)\in (0,1)$ allows for partial violation of a constraint. The values of $d_{i}(i=1,...,m)$ can be carefully selected to create constraints that allow for the desired amount of flexibility.

The above membership functions can be combined into a single piecewise function like the function shown within the Fuzzy Logic section of this page.

$u_{i}(x)={\begin{cases}1,\qquad \qquad \quad \ if\ g_{i}(x)\leq b_{i}\\1-{\frac {g_{i}(x)-b_{i}}{d_{i}}},\quad if\ b_{i}<g_{i}(x)\leq b_{i}+d_{i}\\0,\qquad \qquad \quad \ if\ g_{i}(x)>b_{i}+d_{i}\end{cases}}$

The optimal solution then becomes the value of x that provides the highest degree of membership while satisfying all constraints expressed by the above fuzzy sets. or $maximize\ u_{D}(x)=min\ u_{i}(x)$ [4].

Applications

Fuzzy Programming can be applied in a number of fields including media selection in advertising, automated braking in cars, water resource management, and control systems in HVAC systems [4].

Example

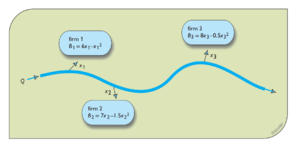
This example is in relation to maximizing the water allocation to three separate firms from a single source, being a river. ${\textstyle TB(X)=(6x_{1}-(x_{1})^{2})+(7x_{2}-(1.5x_{2})^{2})+(8x_{3}-(0.5x_{3})^{2})}$

The total allocation of water for these three firms cannot exceed the total amount of water available, which will be represented by the variable Q. Deducted from that total will be the amount of water that has to remain in the river, R. So Q-R=K, will give us an idea of the water that can be allocated to the firms. in this problem, we will set the variable K to 6. Thus, ${\textstyle x_{1}+x_{2}+x_{3}\leq 6}$. With that constraint, the optimal solution will be $x_{1}=1,x_{2}=1,andx_{3}=4,givingavalueof34.5forTB(X)$. A fuzzy variant of this model would be when each firm's benefits are maximized. The first step is adding a new factor involving the membership function for each of the firms, which can be summed up into the following equation:

$m(X)=[(6x_{1}-x_{1}^{2})+(7x_{2}-1.5x_{2}^{2})+(8x_{3}-0.5x_{3}^{2})]/49.17$

This has a similar constraint compared to the linear version in regards to the total water, ${\textstyle x_{1}+x_{2}+x_{3}\leq 6}$. The optimal solution is same as the linear variant and the degree of satisfaction is m(X)=0.7. Things begin to change when the total amount of units of water becomes more or less 6 units instead of just a crisp 6. The membership function modifies that 2nd constraint into this:

$m_{c}(X)=1ifx_{1}+x_{2}+x_{3}\leq 5m_{c}(X)=[7-(x_{1}+x_{2}+x_{3})]/2ifx_{1}+x_{2}+x_{3}\leq 5m_{c}(X)=0ifx_{1}+x_{2}+x_{3}\geq 7$

Thus the overall optimization problem changes to:

$m_{G}(X)=[(6x_{1}-x_{1}^{2})+(7x_{2}-1.5x_{2}^{2})+(8x_{3}-0.5x_{3}^{2})]/49.17m_{C}(X)=[7-(x_{1}+x_{2}+x_{3})]/2$

This results in $x_{1}=0.91,x_{2}=0.94,x_{3}=3.81,m(X)=0.67,andthetotalbenefitbeingTB(X)=33.1$. This is different from the linear answer in that the total benefit is lower.

Conclusion

The optimization technique of Fuzzy Programming is useful when qualitative adjectives are the only available descriptors for a system's performance criteria/parameters and decision variables.

References

[1] https://ecommons.cornell.edu/bitstream/handle/1813/2804/05_chapter05.pdf?sequence=16&isAllowed=y [2] https://books.google.com/books?id=IkajJC9iGxMC&pg=PA73#v=onepage&q&f=false [3] https://www.mathworks.com/help/fuzzy/foundations-of-fuzzy-logic.html#:~:text=northern%20hemisphere%20climates).-,Membership%20Functions,name%20for%20a%20simple%20concept

[4] http://www.worldacademicunion.com/journal/jus/jusVol01No2paper03.pdf