Generalized Benders decomposition (GBD)
This web page is a duplicate of https://optimization.mccormick.northwestern.edu/index.php/Generalized_Benders_decomposition_(GBD)
Authors: Yuanxi Zhao (ChE 345 Spring 2015)
Steward: Dajun Yue, Fengqi You
Date Presented: May 22, 2015
Generalized Benders Decomposition is a procedure to solve certain types of NLP and MINLP problems. The use of this procedure has been recently suggested as a tool for solving process design problems. While analyzing the solution of nonconvex problems through different implementations of the GBD, it is demonstrated that in certain cases only local minima may be found, whereas in other cases not even convergence to local optima can be achieved.
Introduction
J.F. Benders devised an approach for exploiting the structure of mathematical programming problems with complicating variables (variables which, when temporarily fixed, render the remaining optimization problem considerably more tractable).The algorithm he proposed for finding the optimal value of this vector employs a cutting-plane approach for building up adequate representations of (i) the extremal value of the linear program as a function of the parameterizing vector and (ii) the set of values of the parameterizing vector for which the linear program is feasible. Linear programming duality theory was employed to derive the natural families of cuts characterizing these representations, and the parameterized linear program itself is used to generate what are usually deepest cuts for building up the representations.
Geoffrion (1972) generalized the approach proposed by Benders (1962) to a broader class of optimization problems in which the parametrized subproblem need no longer be a linear program. Nonlinear convex duality theory is employed to derive the natural families of cuts corresponding to those in Bender's case.
Model Formulation
Target problem
,
under the following assumptions:
- and are compact.
- For all , and are convex on .
- For fixed to any feasible , the problem satisfies Slater's condition.
The following problem is equivalent to above and is called its projection on
where { for some }.
For problems where is a convex set, and the functions , are convex with respect to the variable , Geooffrion (1972) proposed a decomposition of (2) based on the following two problems:
Primal problem
where is an arbitrary but fixed point in .
Master problem
{}
{},
where {} , ,
Some Remark
Before any further analysis, it is appropriate to point out that the master problem is equivalent to the projection (2), only when is a convex set, and the functions are convex with respect to . This is so because the dual of , as defined in (2), was invoked in arriving at the Master problem. Therefore, when is not a convex set and/or convexity of the functions and in the variable does not hold, a dual gap may exist between and its dual. In these cases, since by the weak duality theorem, the solution of is always greater than or equal to the solution of its dual, the master problem can only provide a lower bound on the optimum, i.e.
{}
}
}
{},
Solution approaches
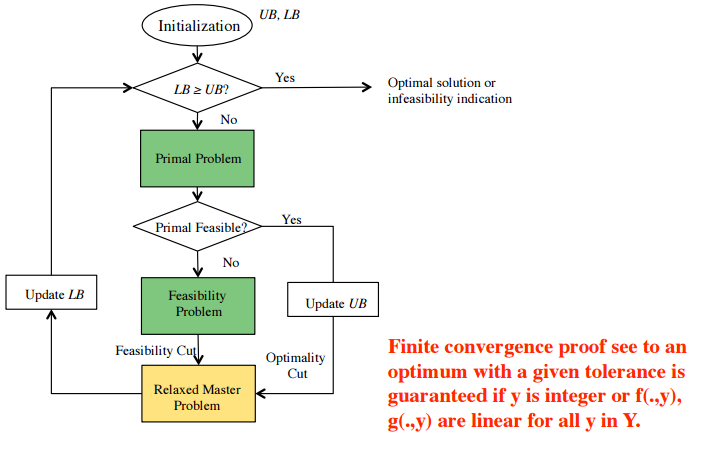
Algorithm flowchart
Computational implementation
The master problem can be rewritten as
{
},
{},
Geoffrion (1972) suggests to solve a relaxed version of this problem in which all but a few constraints are ignored. Since constraints are continuously added to the master, the optimal values of this problem form a monotone nonedecreasing sequence. When and are convex in and certain conditions hold, the lowest solution of the primal and the global solution of the master [as defined from above] will approach one another and will thus provide the global optimum of the overall problem within a prespecified tolerance. As analyzed earlier, when convexity in does not hold, dual gaps may prevent these two values from approaching each other. Nevertheless the global solution of the relaxed master will still provide a valid lower bound on the global optimum of the overall problem. The resulting computational procedure is the following:
Step 1. Let a point in be known. Solve the primal problem and obtain the optimal solution , and the optimal multiplier vector . Put the counters ,. Set , select a tolerance and put . Finally, determine the function .
Step 2. Solve globally the current relaxed master problem:
,
,
Step 3. Solve globally the primal problem using .
Step 3a. Primal is feasible. If terminate. Otherwise, determine the optimal multiplier vector,increase by one, set .Additionally, if ,put . Finally, determine the function and return to Step 2.
Step 3b. Primal is infeasible. Determine a set of values of which satisfy
{}
Increase by one, put and determine the function . Return to Step 2.
When referring to "solutions" of nonconvex optimization problems it is sometimes understood that these may be locally, rather than globally, optimal points. In the above computational procedure it is necessary that the master be solved globally. When problems are jointly convex in and , the master is convex and globality is then achieved. Global solutions of the primal are also needed if convexity of X and/or convexity of and/or in does not hold.
Determination of lambda*
The determination of in Step 3b can be done by any Phase I algorithm. In particular Floudas et al (1989) proposed to solve the following problem:
where .
Since the primal problem is infeasible, it is already known that the solution of this problem is positive. Once this problem is solved and a stationary point is obtained, the following necessary Kuhn-Tucker conditions are satisfied:
From them it is concluded that by solving the problem the condition is satisfied. Note that in this step it is not imperative to achieve globality.
Explicit determination of L
In most cases, the function and are implicitly defined. One case in which these functions can be obtained in explicit form is when the global minimum over can be obtained independently of . i.e. when Property (P) is satisfied. Two examples in which this property is satisfied arise when the functions and are separable in and , and in the variable factor programming case.
Once Property (P) holds, evalution of simply requires that the minima in the master problem be global. This is the so called L-Dual-Adequacy property, which upon satisfaction of Property (P) can be achieved only if a global search of the solution of both
{} {}
is conducted.
Another case in which these functions can be obtained in explicit form is when Property (P') is satisfied, i.e. when the globally optimal solution of the primal, , is also the solution of the minimization of the problems defined in the master problem. This is guaranteed when and are convex and separable in x.
If Property (P') is simply assumed, then this implementation of Generalized Benders Decomposition may only be used, without guarantees, to identify candidates for local, but not global minima.
The above discussion does not mean that Properties (P) and/or (P') must always hold. Other procedures may exist in which the Master problem can be solved without using these requirements.
Advantages and Disadvantages of the algorithm
The GBD method is similar in nature to the Outer-Approximation method. The difference arises in the definition of the MILP master problem (M-MIP). In the GBD method only active inequalities are considered and the set is is disregarded. In particular, assume an outer approximation given at a given point , where for a fixed the point corresponds to the optimal solution to the problem. Making use of the Karush-Kuhn-Tucker conditions and eliminating the continuous variables x, the inequalities can be reduced to Lagrangrian cut projected in the y-space. This can be interpreted as a surrogate constraint because it is obtained as a linear combination of these.
For the case where there is no feasible solution to the problem, if the point is obtained from the feasibility subproblem (NLPF), the feasibility cut projected in y can be obtained using a similar procedure. In this way, the problem (M-MIP) reduces to a problem projected in the y-space. Since the master problem can be derived from the master problem of the Outer-Approximation algorithm in the context of problem. GBD can be regarded as a particular case of the Outer Approximation algorithm. In fact the following property, holds between the two methods:
Property 1. Given the same set of K subproblems, the lower bound predicated by the relaxed master problem (RM-OA) is greater or equal to the one predicted by the relaxed master problem (RM-GBD).
The above proof follows from the fact that the Lagrangian and feasibility cuts, and , are surrogates of the outer approximations . Given the fact that the lower bounds of GBD are generally weaker, this method commonly requires a large number of cycles or major iterations. As the number of 0-1 variables increases this differences become more pronounced. This is to be expected since only one new cut is generated per iteration. Therefore, user-supplied constraints must often be added to the master problem to strengthen the bounds. As for the OA algorithm, the trade-off is that while is generally predicts stronger lower bounds than GBD, the computational cost for solving the master problem (M-OA) is greater since the number of constraints added per iteration is equal to the number of nonlinear constraints plus the nonlinear objective.
The following convergence property applies to the GBD method:
Property 2. If problem (PI) has zero integrality gap, the GBD algorithm converges in one iteration once the optimal is found.
The above property implies that the only case one can expect the GBD method to terminate in one iteration, is when the initial discrete vector is the optimum, and when the objective value of the NLP relaxation of problem (P1) is the same as the objective of the optimal mixed-integer solution. Given the relationship of GBD with the OA algorithm, Property 2 is also inherited by the OA method.
One further property that relates the OA and GBD algorithms is the following:
Property 3. The cut obtained from performing one Benders iteration on the MILP master (RM-OA) is equivalent to the cut obtained from the GBD algorithm.
By making use of this property, instead of solving the MILP (RM-OA) to optimality, for instance by LP-based brand and bound, one can generate a GBD cut by simply performing one Benders iteration on the MILP. This property will prove to be useful when deriving a logic-based version of the GBD algorithm. With the above in mind, the advantages and disadvantages of GBD can thus be summarized as below:
Advantages: Geoffrion (1972) generalized Benders approach to a broader class of programs in which the parameterized subproblem need no longer be a linear program. Nonlinear convex duality theory was employed to derive the quivalent masster problem. In GBD, the algorithm alternates between the solution of relaxed master problems and convex nonlinear subproblems. It is a helpful tool for solving process design problems.
Disadvantages: Some restrictions regarding the convexity and other properties of the function involved were identified. Also, it is found that in certain cases only local minima may be found, whereas in other cases not even convergence to local optima can be achieved. These suggests that the procedure should be used with caution, especially when global optimality is being sought. More specifically, it is demonstrated that the implementation of the procedure guarantees globality when certain properties are satisfied (primal convexity, global solution of the master, Property (P) and L-Dual-Ade-quacy).
Application
Generalized Benders decomposition has been applied to a variety of problems that were modeled as mixed integer linear programming (MDLP) or mixed integer nonlinear programming (MINLP) problems. Geoffrion and Graves (1974) were among the first to use the algorithm to solve an MILP model for the design industrial distribution systems. Noonan and Giglio (1977) used Benders decomposition coupled with a successive linearization procedure to solve a nonlinear multiperiod mix integer model for planning the expansion of electric power generation networks. Rouhani et aL (1985) used GBD to solve an MINLP model for reactive source planning in power systems. Floudas and Ciric (1989) applied GBD to their MINLP formulation for heat exchanger network synthesis. EL-Halwagi and Manouthiosakis (1989) developed an MINLP model for the design and analysis of mass exchange networks and suggested the use of GBD for its solution. Sahinidis and Grossman (1990) applied the algorithm to the problem of scheduling multiproduct parallel production lines by solving the corresponding large scale MINLP model. The technique has also been used for solving nonconvex nonlinear programming (NLP) and MINLP problems: Geoffrion (1971) applied it to the variable factor programming problem and Floudas et aL (1989) suggested a Benders-based procedure for searching for the global optimum of nonconvex problems.
Unfortunately, Benders decomposition has not been uniformly successful in all its application Florial et aL (1976) have noticed that the algorithm often converged very slowly when applied to their MILP model for scheduling the movement of railway engines. Bazaraa and Sherali (1980) observed that a large number of iterations were needed to solve their MILP model for quadratic assignment problems of realistic size. Sahinidis et aL (1989) have found brand and bound to be significantly faster than Benders decomposition for the solution of their multiperiod MILP for long range planning in the chemicla industries. Finally, with respect to the application of GBD to nonconvex problems, in contrast to Geoffrion (1972) and Floudas et aL (1989), Sahinidis and Grossmann (1989) have encountered cases where the application of this technique to their MINLP model for the planning of chemical processes fail to produce the global optima of these problems.
Sources
- Geoffrion, A. M., Elements of Large-Scale Mathematical Programming, Management Science, Vol. 16, No. 11, 1970.
- BENDERS, J. F., Partitioning Procedures for Solving ~lixed-Variables Programming Problems, Numerische Mathematik, Vol. 4, 1962.
- WILSON, R. Programming Variable Factors, Management Science, VoI. 13, No. 1, 1966.
- Balas, E., Duality in Discrete Programming: IV. Applications, CarnegieMellon University, Graduate School of Industrial Administration, Report No. 145, 1968.
- Meyer, R., The Validity of a Family of Optimization Methods, SIAM Journal on Control, Vol. 8, No. I, 1970.
- Dantzic, G. B., Linear Programming and Extensions, Princeton University Press, Princeton, New Jersey, 1963.
- Geoffriosi, A. M., Primal Resource-Directive Approaches for Optimizing Nonlinear Decomposable Systems, Operations Research, Vol. 18, No. 3, 1970.
- Hogan, W., Application of a General Convergence Theory for Outer Approximation Algorithms, University of California at Los Angeles, Western Management Science Institute, Working Paper No. 174, 1971.
- Eaves, B. C., and Zangwill, W. I., Generalized Cutting Plane Algorithms, SIAM Journal on Control, Vol. 9, No. 4, 1971.
- Geoffrion, A. M., A New Global Optimization Technique for Gaseous Diffusion Plant Operation and Capital Investment, University of California at Los Angeles, Graduate School of Business Administration, Discussion Paper, 1970.
- Geoffrion A. M., Duality in Nonlinear Programming: £1 Simplified Application-Oriented Development, SIAM Review, Vol. 13, No. 1, 1971.






































![{\displaystyle ]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09196d1f1ab31143bf7d6f1de80a80303db7dd01)


















![{\displaystyle ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604326beb4b48cc622f2e386be688a2c3a8bf86a)



































































![{\displaystyle -\alpha ]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d3716b95f44fa4a93e0c49a6b3da9dc11b06176)













