Markov decision process: Difference between revisions
| Line 25: | Line 25: | ||
A Markov decision process is made up of multiple fundamental elements: the agent, states, a model, actions, rewards, and a policy. The agent is the object or system being controlled that has to make decisions and perform actions. The agent lives in an environment that can be described using states, which contain information about the agent and the environment. The model determines the rules of the world in which the agent lives, in other words, how certain states and actions lead to other states. The agent can perform a fixed set of actions in any given state. The agent receives rewards based on its current state. A policy is a function that determines the agent's next action based on its current state. | A Markov decision process is made up of multiple fundamental elements: the agent, states, a model, actions, rewards, and a policy. The agent is the object or system being controlled that has to make decisions and perform actions. The agent lives in an environment that can be described using states, which contain information about the agent and the environment. The model determines the rules of the world in which the agent lives, in other words, how certain states and actions lead to other states. The agent can perform a fixed set of actions in any given state. The agent receives rewards based on its current state. A policy is a function that determines the agent's next action based on its current state. | ||
MDP | '''MDP Framework:''' | ||
* <math>S</math> : States (<math>s \epsilon S</math>) | * <math>S</math> : States (<math>s \epsilon S</math>) | ||
| Line 40: | Line 40: | ||
As an example, the Markov decision process can be applied to a college student, depicted to the right. In this case, the agent would be the student. The states would be the circles and squares in the diagram, and the arrows would be the actions. In the state that the student is in Class 3, the allowable actions are to Pass or go to the Pub. The model in this case would assign probabilities to each state given the previous state and action. These probabilities are written next to the arrows. Finally the rewards associated with each state are written in red. | As an example, the Markov decision process can be applied to a college student, depicted to the right. In this case, the agent would be the student. The states would be the circles and squares in the diagram, and the arrows would be the actions. In the state that the student is in Class 3, the allowable actions are to Pass or go to the Pub. The model in this case would assign probabilities to each state given the previous state and action. These probabilities are written next to the arrows. Finally the rewards associated with each state are written in red. | ||
The policy, <math>\Pi</math> , is a function that maps actions to states. The policy | '''The Policy''' | ||
The policy, <math>\Pi</math> , is a function that maps actions to states. The policy determines which is the optimal action given the current state to achieve maximize reward. | |||
<math>\Pi : S \rightarrow A </math> | <math>\Pi : S \rightarrow A </math> | ||
There are various methods that can be used for finding the best policy. Each method tries to maximize rewards in some way, but differs in which accumulation of rewards should be maximized. The first method is to choose the action that maximizes the expected reward given the current state. This is the myopic method, which weighs each time-step decision equally. | There are various methods that can be used for finding the best policy. Each method tries to maximize rewards in some way, but differs in which accumulation of rewards should be maximized. The first method is to choose the action that maximizes the expected reward given the current state. This is the myopic method, which weighs each time-step decision equally. Next is the finite-horizon method, which tries to maximize the accumulated reward over a fixed number of time steps. But because many applications may have infinite horizons, meaning the agent will always have to make decisions and continuously try to maximize its reward, another method is commonly used, known as the infinite-horizon method. Most commonly | ||
* Myopic: Maximize <math>E[ | * Myopic: Maximize <math>E[ | ||
</math> | </math> | ||
* Finite-horizon: Maximize | * Finite-horizon: Maximize | ||
* Infinite-horizon: Maximize | |||
Policy: solving policy | Policy: solving policy | ||
Revision as of 00:35, 29 November 2020
Author: Eric Berg (eb645)
Requirements:
- An introduction of the topic
- Theory, methodology, and/or algorithmic discussions
- At least one numerical example (step-by-step solution process, like
what you did in the HWs)
- A section to discuss and/or illustrate the applications
- A conclusion section
- References
Introduction
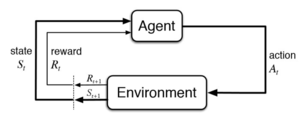
A Markov Decision Process (MDP) is a decision making method that takes into account information from the environment, actions performed by the agent, and rewards in order to decide the optimal next action. MDP works in discrete time, meaning at each point in time the decision process is carried out. The name Markov refers to the Russian mathematician Andrey Markov, since the Markov Decision Process is based on the Markov Property. MDPs are often used as control schemes in machine learning applications. Machine learning can be divided into three main categories: unsupervised learning, supervised learning, and reinforcement learning. The Markov decision process is used as a method for decision making in the reinforcement learning category. MDPs are the basis by which the machine makes decisions and "learns" how to behave in order to achieve its goal.
Theory and Methodology
A Markov Decision process makes decisions using information about the system's current state, the actions being performed by the agent and the rewards earned based on states and actions.
A Markov decision process is made up of multiple fundamental elements: the agent, states, a model, actions, rewards, and a policy. The agent is the object or system being controlled that has to make decisions and perform actions. The agent lives in an environment that can be described using states, which contain information about the agent and the environment. The model determines the rules of the world in which the agent lives, in other words, how certain states and actions lead to other states. The agent can perform a fixed set of actions in any given state. The agent receives rewards based on its current state. A policy is a function that determines the agent's next action based on its current state.
MDP Framework:
- : States ()
- : Actions ()
- : Model determining transition probabilities
- : Reward
In order to understand how the Markov Decision Process works, first the Markov Property must be defined. The Markov Property states that the future is independent of the past given the present. In other words, only the present in needed to determine the future, since the present contains all necessary information from the past. The Markov Property can be described in mathematical terms below:
The above notation conveys that the probability of the next state given the current state is equal to the probability of the next state given all previous states. The Markov Property is relevant to the Markov Decision Process because only the current state is inputted into the policy function to determine the next action, the previous states and actions are not needed.
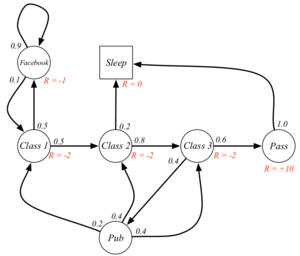
As an example, the Markov decision process can be applied to a college student, depicted to the right. In this case, the agent would be the student. The states would be the circles and squares in the diagram, and the arrows would be the actions. In the state that the student is in Class 3, the allowable actions are to Pass or go to the Pub. The model in this case would assign probabilities to each state given the previous state and action. These probabilities are written next to the arrows. Finally the rewards associated with each state are written in red.
The Policy
The policy, , is a function that maps actions to states. The policy determines which is the optimal action given the current state to achieve maximize reward.
There are various methods that can be used for finding the best policy. Each method tries to maximize rewards in some way, but differs in which accumulation of rewards should be maximized. The first method is to choose the action that maximizes the expected reward given the current state. This is the myopic method, which weighs each time-step decision equally. Next is the finite-horizon method, which tries to maximize the accumulated reward over a fixed number of time steps. But because many applications may have infinite horizons, meaning the agent will always have to make decisions and continuously try to maximize its reward, another method is commonly used, known as the infinite-horizon method. Most commonly
- Myopic: Maximize
- Finite-horizon: Maximize
- Infinite-horizon: Maximize
Policy: solving policy
Algorithms dynamic programming
Example
Numerical Example
Optimizating of a quadratic function.12
Applications
Markov decision Processes have been used widely within reinforcement learning to teach robots or other computer-based systems how to do something they previously were unable to do. For example, Markov decision processes have been used to teach a computer how to play computer games like Pong, Pacman, or Alpha Go. MDPs have been used to teach a simulated robot how to walk and run.
Conclusion
References
Ashraf, M. (2018, April 11). Reinforcement Learning Demystified: Markov Decision Processes (Part 1). Medium. https://towardsdatascience.com/reinforcement-learning-demystified-markov-decision-processes-part-1-bf00dda41690






![{\textstyle P[S_{t+1}|S_{t}]=P[S_{t+1}|S_{1},S_{2},S_{3}...S_{t}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75ef438d698845bb28d52f2e38468979d654bbfc)


