McCormick envelopes: Difference between revisions
m (added figure references) |
(added figures) |
||
| Line 4: | Line 4: | ||
Optimization of a non-convex function f(x) is challenging since it may have multiple locally optimal solutions or no solution and it can take a significant amount of time, resources, and effort to determine if the solution is global or the problem has no feasible solution. According to Castro<sup>1</sup>, "Gradient based solvers [are] unable to certify optimality<sup>"</sup>. Different techniques are used to address this challenge depending on the characteristics of the problem. One technique used is convex envelopes<sup>2</sup>: | Optimization of a non-convex function f(x) is challenging since it may have multiple locally optimal solutions or no solution and it can take a significant amount of time, resources, and effort to determine if the solution is global or the problem has no feasible solution. According to Castro<sup>1</sup>, "Gradient based solvers [are] unable to certify optimality<sup>"</sup>. Different techniques are used to address this challenge depending on the characteristics of the problem. One technique used is convex envelopes<sup>2</sup>: | ||
Given a non-convex function f(x), g(x) is a convex envelope of f(x) for X <math>\in</math> | [[File:Overestimator and underestimator diagram 1.png|thumb|Figure 1: (reproduction from You, F. <sup>2</sup>) depicts relationship of concave over-estimator and convex under-estimator to the function. ]] | ||
Given a non-convex function f(x), g(x) is a convex envelope of f(x) for X <math>\in</math> | |||
· g(x) is convex under-estimator of f(x) | · g(x) is convex under-estimator of f(x) | ||
· | · g(x)>=h(x) for all convex under-estimators h(x) | ||
the | Figure 1 (reproduction from You, F.<sup>2</sup>) depicts the relationship between a function f(x) and the concave over-estimator and | ||
envelope is the tightest possible | the convex under-estimator. A concave envelope is the tightest possible concave over-estimator of a function and a convex | ||
concave and convex envelopes. | envelope is the tightest possible convex under-estimator of a function. Figure 2 (reproduction from You. F.<sup>2</sup>) depicts the | ||
concave and convex envelopes. | |||
[[File:Concave and convex envelopes.png|thumb|Figure 2: (reproduction from You, F.<sup>2</sup>) depicts the relationship of the concave envelope and the convex envelope to the function. ]] | |||
Revision as of 08:30, 26 November 2021
Author: Susan Urban (smu29) (SYSEN 5800 Fall 2021)
Introduction
Optimization of a non-convex function f(x) is challenging since it may have multiple locally optimal solutions or no solution and it can take a significant amount of time, resources, and effort to determine if the solution is global or the problem has no feasible solution. According to Castro1, "Gradient based solvers [are] unable to certify optimality". Different techniques are used to address this challenge depending on the characteristics of the problem. One technique used is convex envelopes2:
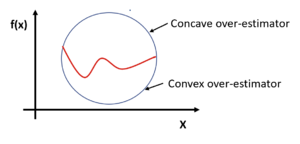
Given a non-convex function f(x), g(x) is a convex envelope of f(x) for X
· g(x) is convex under-estimator of f(x)
· g(x)>=h(x) for all convex under-estimators h(x)
Figure 1 (reproduction from You, F.2) depicts the relationship between a function f(x) and the concave over-estimator and
the convex under-estimator. A concave envelope is the tightest possible concave over-estimator of a function and a convex
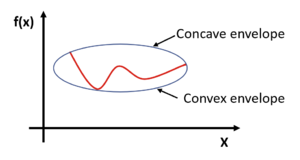
envelope is the tightest possible convex under-estimator of a function. Figure 2 (reproduction from You. F.2) depicts the
concave and convex envelopes.
McCormick Envelopes
In particular, for bilinear (e.g., x*y, x+y) non-linear programming (NLP) problems3, the McCormick Envelope4 is a type of convex relaxation used for optimization.
In case of an NLP, a linear programming (LP) relaxation is derived by replacing each bilinear term with a new variable and adding four sets of constraints. In the case of a mixed-integer linear programming (MINLP), a MILP relaxation is derived. This strategy is known as McCormick relaxation.
The LP solution gives a lower bound and any feasible solution gives an upper bound.
As noted by Scott et al5, "McCormick envelopes are attractive due to their recursive nature of their definition, which affords wide applicability and easy implementation computationally. Furthermore, these relaxations are typically stronger than those resulting from convexification or linearization procedures."
Derivation of McCormick Envelopes
The following is a derivation of the McCormick Envelopes:2
where are upper and lower bound values for and , respectively.
The under-estimators of the function are represented by:
The over-estimators of the function are represented by:
Example: Convex Relaxation
The following shows the relaxation of a non-convex problem:2
Original non-convex problem:
Replacing
we obtain a relaxed, convex problem:
Good bounds are essential to focus and minimize the feasible solution space and to reduce the number of iterations to find the optimal solution. "Good bounds may be obtained either by inspection or solving the optimization problem to minimize (maximize) x, subject to the same constraints as the original problem."2
As discussed by Hazaji6, global optimization solvers implement bound contraction techniques and once the boundary is optimized, domain partitioning may become necessary. Spatial branch and bound schemes7,8 are among the most effective partitioning methods in global optimization. By dividing the domain of a given variable, the solver is able to divide the original domain into smaller regions, further tightening the convex relaxations of each partition.
Example: Numerical
Using GAMS, the solution is z= -24, x=6, y=2.
GAMS code sample:
variable z;
positive variable x, y, w;
equations obj, c1, c2, c3, c4, c5 ;
obj.. z =e= -w -2*x ;
c1.. w =l= 12 ;
c2.. w =g= 0;
c3.. w =g= 6*y +3*x -18;
c4.. w =l= 6*y;
c5.. w =l= 3*x;
x.up = 10;
x.lo =0;
y.up = 2;
y.lo = 0;
model course5800 /all/;
option mip = baron;
option optcr = 0;
solve course5800 minimizing z using mip ;
Application
"Bilinear expressions are the most common non-convex components in mathematical formulations modeling problems in: 6
Chemical engineering 9
Process network problems10"
Computer vision 11
Super resolution imaging 12
Conclusion
McCormick Envelopes provide a relaxation technique for bilinear non-convex nonlinear programming problems3. Since non-convex NLPs are challenging to solve and may require a significant amount of time, resources, and effort to determine if the solution is global or the problem has no feasible solution. McCormick Envelopes provide a straightforward technique that may be applied to bilinear expressions from multiple application areas.
References
- Castro, Pedro. "A Tighter Piecewise McCormick Relaxation for Bilinear Problems." (n.d.): June 2014. Web. 6 June 2015. Retrieved from: <http://minlp.cheme.cmu.edu/2014/papers/castro.pdf
- You, F. (2021). Lecture on Mixed Integer Non-Linear Programming (MINLP). Archives for SYSEN 5800 Computational Optimization (2021FA), Cornell University, Ithaca, NY.
- Dombrowski, J. (2015, June 7). Northwestern University Open Text Book on Process Optimization, McCormick Envelopes Retrieved from https://optimization.mccormick.northwestern.edu/index.php/McCormick_envelopes
- McCormick, Garth P. Computability of Global Solutions To Factorable Nonconvex Solutions: Part I: Convex Underestimating Problems
- Scott, J. K. Stuber, M. D. & Barton, P. I. (2011). Generalized McCormick Relaxations. Journal of Global Optimization, Vol. 51, Issue 4, 569-606 doi: 10.1007/s10898-011-9664-7
- Hijazi, H., Perspective Envelopes for Bilinear Functions, unpublished manuscript, retrieved from: Perspective Envelopes for Bilinear Functions
- Androulakis, I., Maranas, C., Floudas, C.: alphabb: A global optimization method for general constrained nonconvex problems. Journal of Global Optimization 7(4), 337{363 (1995)
- Smith, E., Pantelides, C.: A symbolic reformulation/spatial branch-and-bound algorithm for the global optimisation of nonconvex fMINLPsg. Computers & Chemical Engineering 23(4), 457 { 478 (1999)
- Geunes, J., Pardalos, P.: Supply chain optimization, vol. 98. Springer Science & BusinessMedia (2006)
- Nahapetyan, A.: Bilinear programming: applications in the supply chain management bilinear programming: Applications in the supply chain management. In: C.A. Floudas, P.M. Pardalos (eds.) Encyclopedia of Optimization, pp. 282{288. Springer US (2009)
- Chandraker, M. & Kriegman, D. (n.d.): Globally Optimal Bilinear Programming for Computer Vision Applications. University of San Diego, CA. Retrieved from: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwis69Say7H0AhXWp3IEHVGLBW4QFnoECC4QAQ&url=http%3A%2F%2Fvision.ucsd.edu%2F~manu%2Fpdf%2Fcvpr08_bilinear.pdf&usg=AOvVaw1h-cpWO81s41howVxYKq7F
- Gronski, J. (2019). Non-Convex Optimization and Applications to Bilinear Programming and Super-Resolution Imaging. University of Colorado. Retrieved from: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwif3qO017H0AhWNknIEHebkAhMQFnoECA0QAQ&url=https%3A%2F%2Fscholar.colorado.edu%2Fdownloads%2Fwd375w61z&usg=AOvVaw09lnJJoZX3i_wwBGHin9LK




































