McCormick envelopes: Difference between revisions
(updated the digram) |
(corrected superscripts) |
||
| Line 7: | Line 7: | ||
== '''McCormick Envelopes: Theory, Methodology and Algorithmic Discussions''' == | == '''McCormick Envelopes: Theory, Methodology and Algorithmic Discussions''' == | ||
The McCormick Envelope<sup> | The McCormick Envelope, originally developed by Garth McCormick<sup>1</sup>, is a type of convex relaxation used for the optimization of bilinear (e.g., x*y, x+y) non-linear programming (NLP) problems. | ||
Each bilinear term is replaced with a new variable and four sets of constraints are added. The non-linear programming is converted to a relaxed convex linear programming which can be more easily solved. | Each bilinear term is replaced with a new variable and four sets of constraints are added. The non-linear programming is converted to a relaxed convex linear programming (LP) which can be more easily solved. | ||
The LP solution gives a lower bound and any feasible solution gives an upper bound. | The LP solution gives a lower (L) bound and any feasible solution to the problem gives an upper (U) bound. | ||
As noted by Scott et | As noted by Scott et al2, McCormick envelopes are effective since they are recursive, can be applied to a variety of applications, and are typically stronger than those resulting from convexification or linearization procedures. | ||
The following is a derivation of the McCormick Envelopes: | The following is a derivation of the McCormick Envelopes: | ||
| Line 113: | Line 113: | ||
Good lower and upper bounds focus and minimize the feasible solution space; they reduce the number of iterations to find the optimal solution. | Good lower and upper bounds focus and minimize the feasible solution space; they reduce the number of iterations to find the optimal solution. | ||
As discussed by | As discussed by Hazaji3, global optimization solvers focus initially on optimizing the lower and upper bounds, and when necessary, focus on domain partitioning. By dividing the domain of a given variable into partitions or smaller regions, the solver is able to tailor and further tighten the convex relaxations of each partition. | ||
== '''Example: Numerical''' == | == '''Example: Numerical''' == | ||
Revision as of 16:20, 27 November 2021
Author: Susan Urban (smu29) (SYSEN 5800 Fall 2021)
Introduction
Optimization of a non-convex function f(x) is challenging since it may have multiple locally optimal solutions or no solution and it can take a significant amount of time, computing resources, and effort to determine if the solution is global or the problem has no feasible solution. Different techniques are used to address this challenge depending on the characteristics of the problem.
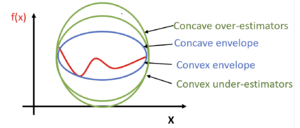
One technique used for a given non-convex function is the identification of a concave envelope and a convex envelope. The concave envelope, and respectively the convex envelope, is the concave over-estimator and convex under-estimator for the given function providing the tighest fit to the given function. The envelope surrounds the given function, like an envelope encloses a letter, and limits the feasible solution space the most in comparison to all other concave over-estimators and convex under-estimators. Multiple concave over-estimators and multiple convex under-estimators may exist but there is only one concave envelope and one convex envelope for a given function and domain.
McCormick Envelopes: Theory, Methodology and Algorithmic Discussions
The McCormick Envelope, originally developed by Garth McCormick1, is a type of convex relaxation used for the optimization of bilinear (e.g., x*y, x+y) non-linear programming (NLP) problems.
Each bilinear term is replaced with a new variable and four sets of constraints are added. The non-linear programming is converted to a relaxed convex linear programming (LP) which can be more easily solved.
The LP solution gives a lower (L) bound and any feasible solution to the problem gives an upper (U) bound.
As noted by Scott et al2, McCormick envelopes are effective since they are recursive, can be applied to a variety of applications, and are typically stronger than those resulting from convexification or linearization procedures.
The following is a derivation of the McCormick Envelopes:
where are upper and lower bound values for and , respectively.
The under-estimators of the function are represented by:
The over-estimators of the function are represented by:
The following shows the relaxation of a non-convex problem:
Original non-convex problem:
Replacing
we obtain a relaxed, convex problem:
Good lower and upper bounds focus and minimize the feasible solution space; they reduce the number of iterations to find the optimal solution.
As discussed by Hazaji3, global optimization solvers focus initially on optimizing the lower and upper bounds, and when necessary, focus on domain partitioning. By dividing the domain of a given variable into partitions or smaller regions, the solver is able to tailor and further tighten the convex relaxations of each partition.
Example: Numerical
Using GAMS, the solution is z= -24, x=6, y=2.
GAMS code sample:
variable z;
positive variable x, y, w;
equations obj, c1, c2, c3, c4, c5 ;
obj.. z =e= -w -2*x ;
c1.. w =l= 12 ;
c2.. w =g= 0;
c3.. w =g= 6*y +3*x -18;
c4.. w =l= 6*y;
c5.. w =l= 3*x;
x.up = 10;
x.lo =0;
y.up = 2;
y.lo = 0;
model course5800 /all/;
option mip = baron;
option optcr = 0;
solve course5800 minimizing z using mip ;
Application
Bilinear functions occur in numerous engineering and natural science applications where McCormick Envelopes can be utilized, including the following :
Computer vision 4
Super resolution imaging 5
Energy conversion networks 6
Cellular networks7
Dynamic biological systems8
Conclusion
Non-convex NLPs are challenging to solve and may require a significant amount of time, computing resources, and effort to determine if the solution is global or the problem has no feasible solution. McCormick Envelopes provide a relaxation technique for bilinear non-convex nonlinear programming problems. McCormick Envelopes provide a straightforward technique of replacing each bilinear term with a new variable and adding four constraints. Due to the recursive nature of this technique, it may be applied to a wide variety of engineering and scientific applications involving bilinear terms.
References
- McCormick, Garth P. Computability of Global Solutions To Factorable Nonconvex Solutions: Part I: Convex Underestimating Problems
- Scott, J. K. Stuber, M. D. & Barton, P. I. (2011). Generalized McCormick Relaxations. Journal of Global Optimization, Vol. 51, Issue 4, 569-606 doi: 10.1007/s10898-011-9664-7
- Hijazi, H., Perspective Envelopes for Bilinear Functions, unpublished manuscript, retrieved from: Perspective Envelopes for Bilinear Functions
- Chandraker, M. & Kriegman, D. (n.d.): Globally Optimal Bilinear Programming for Computer Vision Applications. University of San Diego, CA. Retrieved from: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwis69Say7H0AhXWp3IEHVGLBW4QFnoECC4QAQ&url=http%3A%2F%2Fvision.ucsd.edu%2F~manu%2Fpdf%2Fcvpr08_bilinear.pdf&usg=AOvVaw1h-cpWO81s41howVxYKq7F
- Gronski, J. (2019). Non-Convex Optimization and Applications to Bilinear Programming and Super-Resolution Imaging. University of Colorado. Retrieved from: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwif3qO017H0AhWNknIEHebkAhMQFnoECA0QAQ&url=https%3A%2F%2Fscholar.colorado.edu%2Fdownloads%2Fwd375w61z&usg=AOvVaw09lnJJoZX3i_wwBGHin9LK
- Kantor, J., & Mousaw, P. (2012). A class of bilinear models for the optimization of energy conversion networks. Chemical Engineering Science, 67, 131-138. doi: 10.1016/j.ces.2011.08.033
- Ahmed, F., Naeem, M., Ejaz, W. et al. Renewable Energy Assisted Sustainable and Environment Friendly Energy Cooperation in Cellular Networks. Wireless Pers Commun 108, 2585–2607 (2019). https://doi.org/10.1007/s11277-019-06539-z
- Miro et al.: Deterministic global optimization algorithm based on outer approximation for the parameter estimation of nonlinear dynamic biological systems. BMC Bioinformatics (2012) 13:90. doi: 10.1186/1471-2105-13-90 ·



































