McCormick envelopes: Difference between revisions
| Line 158: | Line 158: | ||
</math> | </math> | ||
Substituting these values into the original problem and the McCormick Envelopes, the problem is reformulated: | Substituting these values into the original problem and the McCormick Envelopes, the problem is reformulated: | ||
| Line 167: | Line 169: | ||
<math>s.t. \ w \leq 18</math> | <math>s.t. \ w \leq 18</math> | ||
| Line 181: | Line 184: | ||
</math> | </math> | ||
| Line 198: | Line 202: | ||
</math> | </math> | ||
| Line 215: | Line 220: | ||
</math> | </math> | ||
| Line 229: | Line 235: | ||
</math> | </math> | ||
Using GAMS, the solution is z= -76.2, x=10, y=1.8. | Using GAMS, the solution is z= -76.2, x=10, y=1.8. | ||
| Line 255: | Line 260: | ||
#M. Chandraker and D. Kriegman, "Globally Optimal Bilinear Programming for Computer Vision Applications," presented at the IEEE Computer Society Conference on ''Computer Vision and Pattern Recognition,'' 2008''.'' | #M. Chandraker and D. Kriegman, "Globally Optimal Bilinear Programming for Computer Vision Applications," presented at the IEEE Computer Society Conference on ''Computer Vision and Pattern Recognition,'' 2008''.'' | ||
#J. Kantor and P. Mousaw, "A class of bilinear models for the optimization of energy conversion networks," ''Chemical Engineering Science, vol. 67,'' pp. 131-138, 2012. | #J. Kantor and P. Mousaw, "A class of bilinear models for the optimization of energy conversion networks," ''Chemical Engineering Science, vol. 67,'' pp. 131-138, 2012. | ||
#F. Ahmed, M. Naeem, | #F. Ahmed, M. Naeem, W. Ejaz, M. Iqbal and A. Anpalagan, "Renewable Energy Assisted Sustainable and Environment Friendly Energy Cooperation in Cellular Networks," ''Wireless Personal Commununications'', vol. 108''',''' pp. 2585–2607, 2019. | ||
#Miro et al.: Deterministic global optimization algorithm based on outer approximation for the parameter estimation of nonlinear dynamic biological systems. ''BMC Bioinformatics'' (2012) 13:90. | #Miro et al.: Deterministic global optimization algorithm based on outer approximation for the parameter estimation of nonlinear dynamic biological systems. ''BMC Bioinformatics'' (2012) 13:90. | ||
#Michael B., Castillo, A., Watson, J., & Laird, C. (2018) Strengthened SOCP Relaxations for ACOPF with McCormick Envelopes and Bounds Tightening, ''Computer Aided Chemical Engineering, 44,'' 1555-1560, | #Michael B., Castillo, A., Watson, J., & Laird, C. (2018) Strengthened SOCP Relaxations for ACOPF with McCormick Envelopes and Bounds Tightening, ''Computer Aided Chemical Engineering, 44,'' 1555-1560, | ||
Revision as of 16:19, 8 December 2021
Author: Susan Urban (SYSEN 5800 Fall 2021)
Introduction
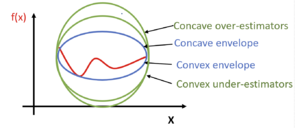
Optimization of a non-convex function f(x) is challenging since it may have multiple locally optimal solutions or no solution and it can take a significant amount of time, computing resources, and effort to determine if the solution is global or the problem has no feasible solution. Different techniques are used to address this challenge depending on the characteristics of the problem. One technique used for a given non-convex function is the identification of a concave envelope and a convex envelope. The concave envelope, and respectively the convex envelope, is the concave over-estimator and convex under-estimator for the given function providing the tightest fit to the given function. The envelope surrounds the given function, like an envelope encloses a letter, and limits the feasible solution space the most in comparison to all other concave over-estimators and convex under-estimators. Multiple concave over-estimators and multiple convex under-estimators may exist but there is only one concave envelope and one convex envelope for a given function and domain. Figure 1 depicts the relationship between the given function f(x), multiple concave over-estimators, multiple convex under-estimators, a convex envelope, and a concave envelope.
McCormick Envelopes: Theory, Methodology and Algorithmic Discussions
The McCormick Envelope, originally developed by Dr. Garth McCormick1, is a type of convex relaxation used for the optimization of bilinear (e.g., x*y, exy + y, sin (x+y) - x2) non-linear programming (NLP) problems. As McCormick1 noted, McCormick Envelopes are based on the key assumption that convex and concave envelopes can be constructed for the given function.
Each bilinear term is replaced with a new variable and four sets of constraints are added. The non-linear programming is converted to a relaxed convex linear programming (LP) which can be more easily solved.
The LP solution gives a lower (L) bound and any feasible solution to the problem gives an upper (U) bound.
As noted by Scott et al2, McCormick envelopes are effective since they are recursive, can be applied to a variety of applications, and are typically stronger than those resulting from convexification or linearization procedures.
The following is a derivation of the McCormick Envelopes for a given bilinear function:
where are upper and lower bound values for and , respectively.
a and b are both positive resulting in a positive product
substituting w=xy and reformulating the inequality produces
Following the same sequence of steps, the remaining inequalities are produced:
The under-estimators of the function are represented by:
The over-estimators of the function are represented by:
The following shows the relaxation of a non-convex problem using McCormick Envelopes:
The original non-convex problem:
Replacing , we obtain a relaxed, convex problem using McCormick Envelopes:
Similar steps are taken to derive the McCormick Envelopes for given functions with different formats e.g., exy.
Good lower and upper bounds focus and minimize the feasible solution space; they reduce the number of iterations to find the optimal solution.
Piecewise McCormick Relaxation
As discussed by Hazaji3, global optimization solvers focus initially on optimizing the lower and upper bounds, and when necessary, focus on domain partitioning. By dividing the domain of a given variable into partitions or smaller regions, the solver is able to tailor and further tighten the convex relaxations of each partition. This strategy is known as the Piecewise McCormick relaxation4.
Example: Numerical
For the given problem,
Substituting these values into the original problem and the McCormick Envelopes, the problem is reformulated:
Using GAMS, the solution is z= -76.2, x=10, y=1.8.
Applications
Bilinear functions occur in numerous engineering and natural science applications where McCormick Envelopes can be utilized, including the following :
Computer vision 5
Energy conversion networks 6
Cellular networks7
Dynamic biological systems8
Alternate current optimal power flow (ACOPF)9
Conclusion
Non-convex NLPs are challenging to solve and may require a significant amount of time, computing resources, and effort to determine if the solution is global or the problem has no feasible solution. McCormick Envelopes provide a relaxation technique for bilinear non-convex nonlinear programming problems. McCormick Envelopes provide a straightforward technique of replacing each bilinear term with a new variable and adding four constraints. Due to the recursive nature of this technique, it may be applied to a wide variety of engineering and scientific applications involving bilinear terms.
References
- G. P. McCormick, "Computability of Global Solutions To Factorable Nonconvex Solutions: Part I: Convex Underestimating Problems," Mathematical Programming, vol. 10, pp. 147-175, 1976.
- J. K. Scott, M. D. Stuber and P. I. Barton, "Generalized McCormick Relaxations," Journal of Global Optimization, vol. 51, pp. 569-606, 2011.
- H. Hijazi, "Perspective Envelopes for Bilinear Functions"
- M. Bergamini, P. Aguirre, and I. Grossman, "Logic-based outer approximation for globally optimal synthesis of process networks," Computers and Chemical Engineering, vol. 29, pp. 1914–1933, 2005.
- M. Chandraker and D. Kriegman, "Globally Optimal Bilinear Programming for Computer Vision Applications," presented at the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2008.
- J. Kantor and P. Mousaw, "A class of bilinear models for the optimization of energy conversion networks," Chemical Engineering Science, vol. 67, pp. 131-138, 2012.
- F. Ahmed, M. Naeem, W. Ejaz, M. Iqbal and A. Anpalagan, "Renewable Energy Assisted Sustainable and Environment Friendly Energy Cooperation in Cellular Networks," Wireless Personal Commununications, vol. 108, pp. 2585–2607, 2019.
- Miro et al.: Deterministic global optimization algorithm based on outer approximation for the parameter estimation of nonlinear dynamic biological systems. BMC Bioinformatics (2012) 13:90.
- Michael B., Castillo, A., Watson, J., & Laird, C. (2018) Strengthened SOCP Relaxations for ACOPF with McCormick Envelopes and Bounds Tightening, Computer Aided Chemical Engineering, 44, 1555-1560,










































