Mixed-integer linear fractional programming (MILFP)
Author: Xiang Zhao (SysEn 6800 Fall 2020)
Steward: Allen Yang, Fengqi You
Introduction
The mixed-integer linear fractional programming (MILFP) is a kind of mixed-integer nonlinear programming (MINLP) that is widely applied in chemical engineering, environmental engineering, and their hybrid field ranging from cyclic-scheduling problems to the life cycle optimization (LCO). Specifically, the objective function of the MINFP is shown as a ratio of two linear functions formed by various continuous variables and discrete variables. However, the pseudo-convexity and the combinatorial nature of the fractional objective function can cause computational challenges to the general-purpose global optimizers, such as BARON, to solve this MILFP problem. In this regard, we introduce the basic knowledge and solution steps of three algorithms, namely the Parametric Algorithm, Reformulation-Linearization method, and Branch-and-Bound with Charnes-Cooper Transformation Method, to efficiently and effectively tackle this computational challenge.
Standard Form and Properties
Consider such standard form of the MILFP:
The properties of the objective function are shown as follows:
- is (strictly) pseudoconcave and pseudoconvex over its domain.
- The local optimality of is the same as its global optimality.
Notably, several nonlinear solvers that can deal with the pseudoconvexity, such as the spatial branch-and-bound (SBB), are capable of solving the MILFP. However, the memory usage of these solvers is enormous when solving a large-scale problem that is applied in industrial scheduling or supply chain optimization project. Hence, we introduce the parametric algorithm, and reformulation-linearization method, which can reformulate the MILFP into the mixed-integer linear programming (MILP) problem, to reduce the memory usage and enhance solution efficiency.
Parametric Algorithm
One way to successively reformulate and solve the MILFP is to apply the parametric algorithm, which can find the global optimality within finite iterations. The linearly parametric form of the reformulated objective function has the advantage of directly finding the global optimality, while the size of the sub-problem remains the same. The reformulation approach is shown as follows:
The original form of the objective function is:
We use a parametric parameter to reformulate the objective function into :
is reformulated into
Notably, the optimal solution of the parametric objective function has only one zero-point, which is the same as its global optimal solution. Hence, we need to find the zero-point iteratively following the approaches below:
- Initialize the parametric parameter . Set the tolerance
- Solve the sub-problem via using CPLEX, whose objective function is with the same original constraints. The optimal solution is .
- Calculate the value of parametric objective function , if the value is within the tolerance , then the optimality is found.
- Update the parametric parameter and redo step 1.
Reformulation-Linearization Method
The reformulation-linearization method, which incorporates the Glover’s linearization into the Charnes-Cooper transformation, introduce auxiliary variables to reformulate the MILFP into equivalent MINLP. The resulting MINLP is subsequently transformed into MILP, which can be efficiently solved by typical MILP solvers like CPLEX, via using Glover’s linearization.The reformulation approach is shown as follows:
The original form of the optimization model is:
Firstly, we convert the fractional objective function into a bilinear constraint, as well as a substutional term :
To get the MILP equivalent model, we use the Glover's Linearization to transform the bilinear constraint ():
is equivalent to
In this regard, we reformulate the original MILFP model into MILP model, which can be effectively solved by typical branch-and-cut solver like CPLEX. To summarize, the reformulated MILP model is shown below:
Branch-and-Bound with Charnes-Cooper Transformation Method
The integration of the Charnes-Cooper transformation method with the Branch-and-Bound (B&B) algorithm can reformulate the relaxation form of the fractional objective problem in each node into an LP subproblem, which can reach its global optimality via using MILP solvers like CPLEX. Since solution steps are similar to those of B&B and the reformulation step is shown in Reformulation-Linearization Method, we encourage readers to search for B&B algorithm and paper of Gao et al.
Application and Modeling for Numerical Examples
Applications of MILFP
Two typical applications are introduced in this section, namely cyclic scheduling and life-cycle optimization. One typical cyclic scheduling problem was illustrated in Yue et al., the fractional objective was optimized to reflect both the absolute profit and scheduling aspect, which were shown in the numerator and denominator, respectively. The combination of Reformulation-Linearization method and CPLEX were regarded as solution algorithm and the optimization framework was applied in a case study corresponding to a multiproduct batch plant that used 14 processing stages for producing three acrylic fiber formulations with a time horizon of 100 h.
In the life-cycle optimization problem of a certain processing system, the unreasonably maximum or minimum treatment amount from optimizing linear objective functions can be avoided via optimizing the fractional objective, and thus the balanced processing amount can be obtained to address the sustainable design and synthesis of this processing system. Notably, the functional unit is shown in the denominator, while the total economic and environmental performances are denoted as numerators in fractional objective functions. Specifically as illustrated in Gong et al., the sustainable design and synthesis of the shale gas processing system was obtained via optimizing the unit net present value (NPV), unit global warming potential (GWP), and unit freshwater consumption simultaneously. The optimization framework was applied in the Marcella Shale gas site.
In the next two numerical examples, we present a “simple form” of MILFP that can be used for selecting optimal processing pathways via maximizing unit NPV or minimizing unit GWP, respectively.
Numerical Examples of MILFP
Introduction of Numerical Examples
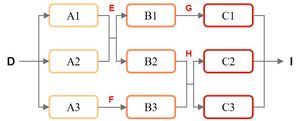
Let’s consider a simple chemical plant, whose superstructure is shown on the right side. The superstructure denotes all technology options, and only one of them in each level can be chosen simultaneously. To find the optimal processing pathway on the basis of economic and environmental aspects, we consider maximizing the net present value (NPV) or minimizing unit greenhouse gas (GHG) emissions, respectively. Notably, the unit NPV equals the ratio of the NPV with the total mass flow rate of product I within the project lifespan of ten years. The discount rate is 10%.
Input Parameters of Numerical Examples
| Processing Level | Conversion Rate | Conversion Rate | Conversion Rate |
|---|---|---|---|
| Level 1 | D to E: 0.8 | D to F: 0.9 | |
| Level 2 | E to G: 0.7 | E to H: 0.8 | F to H: 0.4 |
| Level 3 | G to I: 0.5 | H to I: 0.6 |
| A1 | A2 | A3 | B1 | B2 | B3 | C1 | C2 | C3 |
|---|---|---|---|---|---|---|---|---|
| 6,000,000 | 7,000,000 | 7,500,000 | 5,000,000 | 6,000,000 | 7,500,000 | 11,000,000 | 10,000,000 | 10,500,000 |
| A1 | A2 | A3 | B1 | B2 | B3 | C1 | C2 | C3 |
|---|---|---|---|---|---|---|---|---|
| 50 | 40 | 35 | 60 | 55 | 45 | 30 | 35 | 33 |
| A1 | A2 | A3 | B1 | B2 | B3 | C1 | C2 | C3 |
|---|---|---|---|---|---|---|---|---|
| 25 | 30 | 20 | 30 | 28 | 50 | 27 | 25 | 15 |
| Item | Supply/Demand | Feedstock/Product Price |
|---|---|---|
| D | 2,000,000 | 100 |
| I | 200,000 | 2000 |
| A1 | A2 | A3 | B1 | B2 | B3 | C1 | C2 | C3 |
|---|---|---|---|---|---|---|---|---|
| 1.2 | 0.9 | 0.7 | 1.4 | 1.6 | 1.3 | 2.1 | 2.4 | 2.7 |
Nomenclatures for the Mathematical Model of the Numerical Examples
| Nomenclature | Meaning |
|---|---|
| I | Set of production stages indexed by i. |
| J | Set of process alternatives j. |
| D | Demand of product I. |
| CAVi,j | Unit variable capital cost in the process alternative j at the production stage i. |
| CVi,j | Conversion rate from input flow to output flow in the process alternative j at the production stage i. |
| FIXIi,j | Fixed capital cost in the process alternative j at the production stage i. |
| GHGi,j | Unit GHG emissions from the process alternative j at the production stage i. |
| OPERIi,j | Unit operating cost in the process alternative j at the production stage i. |
| PRI | Price of product I. |
| PRID | Price of chemical D. |
| S | Supply of chemical D. |
| yi,j | 0-1 variable. Equal to one if the process alternative j at the production stage i is selected. |
| cai,j | Capacity of process alternative j at the production stage i. |
| fec | Total feedstock cost. |
| fix | Total fixed capital cost. |
| ghgt | Total GHG emissions. |
| mii,j | Mass flow rate of the feedstock flow to process alternative j at the production stage i. |
| moi,j | Mass flow rate of the output flow to the process alternative j at the production stage i. |
| oper | Total operating cost. |
| objc | Unit net present value (NPV). |
| obje | Unit GHG emissions (within one operating year). |
| npv | Net present value. |
| sale | Total sales. |
| vai | Total variable capital cost. |
Mass Balance Constraints
This aforementioned constraint denotes that the mass flow rate of the inlet flow should not exceed the treatment capacity.
This aforementioned constraint represents that the treatment capacity would be zero if the corresponding technology option is not selected.
This aforementioned constraint illustrates the conversion of the inlet flow and the outlet flow.
This aforementioned constraint denotes that the summation of mass flow rates of the outlet flows from the previous processing level equals to those of the inlet flows in the next processing level.
This aforementioned constraint represents that the summation of mass flow rates of the technology options in the third processing level should be larger than the demand of the product I.
This aforementioned constraint represents that the summation of mass flow rates of the technology options in the first processing level should be less than the supply of the chemical D.
Superstructure Configuration Constraints
Notably, the superstructure configuration constraints illustrate the logic relationship between each technology option within the superstructure. If the binary variable equals to 1, than the technology option in the process level is selected.
Economic Evaluation Constraints
We consider the fixed capital cost (), variable capital cost (), operating cost (), and feedstock cost () as the expenses for the chemical processing system.
The net present value is calculated in the constraint below (), where we account for the total discounted cash flow () and represents for the lifespan of the this project.
Environmental Evaluation Constraint
The total GHG emissions from the chemical processing system is calculated in the constraint below.
Objective Functions
Two numerical examples are presented as optimizing each fractional objective functions, which are shown as below. Since all constraints denote the relationship between various continous and discrete variables, two aforementioned numerical problems can be regarded as MILFPs. We consider maximizing unit NPV () or minimizing unit GWP () in two numerical examples, respectively.
Solution for Numerical Examples
Maximizing Unit NPV
We consider the first objective function () and all constraints in the mathematical model, where we can reformulate the objective function into a parametric form () using parametric parameter :
This reformulated model can be solved by the CPLEX iteratively, and the solution is shown as follows:
| Level 1 | Level 2 | Level 3 |
|---|---|---|
| A1 | - | - |
| - | B2 | - |
| - | - | C3 |
| Production Amount (ton/yr) | Unit NPV ($/ton) | Unit GHG Emissions (ton CO2-eq/ton products) |
|---|---|---|
| 768,000 | 187.75 | 10.18 |
Minimizing Unit GHG Emissions
We consider the first objective function () and all constraints in the mathematical model, where we can reformulate the objective function into a parametric form () using parametric parameter :
This reformulated model can be solved by the CPLEX iteratively, and the solution is shown as follows:
| Level 1 | Level 2 | Level 3 |
|---|---|---|
| - | - | - |
| A2 | B2 | C2 |
| - | - | - |
| Production Amount (ton/yr) | Unit NPV ($/ton) | Unit GHG Emissions (ton CO2-eq/ton products) |
|---|---|---|
| 768,000 | 186.23 | 9.68 |




































































