Network flow problem
Author: Aaron Wheeler, Chang Wei, Cagla Deniz Bahadir, Ruobing Shui, Ziqiu Zhang (CHEME 6800 Fall 2020)
Steward: Allen Yang, Fengqi You
Introduction:
Network flow problems arise in several key instances and applications within society and have become fundamental problems within computer science, operations research, applied mathematics, and engineering. Developments in the approach to tackle these problems resulted in algorithms that became the chief instruments for solving problems related to large-scale systems and industrial logistics. Spurred by early developments in linear programming, the methods for addressing these extensive problems date back several decades and they evolved over time as the use of digital computing became increasingly prevalent in industrial processes. Historically, the first instance of an algorithmic development for the network flow problem came in 1956, with the network simplex method formulated by George Dantzig [ref]. A variation of the simplex algorithm that revolutionized linear programming, this method leveraged the combinatorial structure inherent to these types of problems and demonstrated incredibly high accuracy [ref]. This method and its variations would go on to define the embodiment of the algorithms and models for the various and distinct network flow problems discussed here.
Theory:
Qualitatively, the network flow problem can be conceptualized as a directed graph which abides by certain flow capacity constraints at its edges and equates the values entering and exiting its vertices at all points besides terminal source and sink terms. The vertices in this problem are the origins, destinations, and intermediate points and are referred to as nodes. The edges are the directional transportation links between these nodes and are referred to as arcs [ref]. Models for network flow problems function as tools for computing the net flow of units along these constrained arcs and between pairs of nodes, and are useful for quantifying logistical interests such as the optimal scheme for the distribution of a product from a plant to it’s consumer constituents. In this scenario, the product departs from the distribution source (origin) and travels through a network of intermediary transition points such as warehouses and fulfillment centers (nodes), before finally reaching the consumer market (destination). Along this journey, the transportation method along the route (arc) may be subjected to certain restraints such as the allowable amount of product carried between points (capacity constraints). The objective function in this case would be to minimize the cost of shipping the product whilst still meeting a specified demand. This exact circumstance is very common in industrial logistics and was the primary motivation for defining and solving the network flow problem [ref]. This case, the transportation problem, was the beginning of a wide assortment of problems defined for network flow by leveraging it’s combinatorial structure in a special-purpose algorithm.
Historically, the classic network flow problems are considered to be the maximum flow problem and the minimum-cost circulation problem, the assignment problem, bipartite matching problem, transportation problem, and the transshipment problem [ref]. The approach to these problems become quite specific based upon the problem’s objective function but can be generalized by the following iterative approach: 1. determining the initial basic feasible solution; 2. checking the optimality conditions (i.e. whether the problem is infeasible, unbounded over the feasible region, optimal solution has been found, etc.); and 3. constructing an improved basic feasible solution if the optimal solution has not been determined [ref].
General Applications
The Assignment Problem:
Various real-life instances of assignment problems exist for optimization, such as assigning a group of people to different tasks, events to halls with different capacities, rewards to a team of contributors, and vacation days to workers. All together, the assignment problem is a bipartite matching problem in the kernel. [3] In a classical setting, two types of objects of equal amount are bijective (i.e. they have one-to-one matching), and this tight constraint ensures a perfect matching. The objective is to minimize the cost or maximize the profit of matching, since different items of two types have distinct affinity.
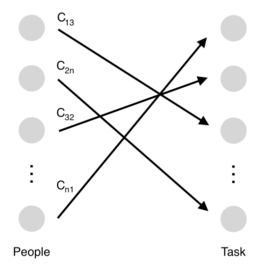
A classic example is as follows: suppose there are n people (set P) to be assigned to n tasks (set T). Every task has to be completed and each task has to be handled by only one person, and cij, usually given by a table, measures the benefits gained by assigning the person i (in P) to the task j (in T). [4] The natural objective here is to maximize the overall benefits by devising the optimal assignment pattern. A graph of the general assignment problem and a table of preference are depicted as Figure 1 and Table 1.
| Benefits | Task 1 | Task 2 | Task 3 | ... | Task n |
|---|---|---|---|---|---|
| Person 1 | 0 | 3 | 5 | ... | 2 |
| Person 2 | 2 | 1 | 3 | ... | 6 |
| Person 3 | 1 | 4 | 0 | ... | 3 |
| ... | ... | ... | ... | ... | ... |
| Person n | 0 | 2 | 3 | ... | 3 |
Figure 1 can be viewed as a network. The nodes represent people and tasks, and the edges represent potential assignments between a person and a task. Each task can be completed by any person. However, the person that actually ends up being assigned to the task will be the lone individual who is best suited to complete. In the end, the edges with positive flow values will be the only ones represented in the finalized assignment. [5]
To approach this problem, the binary variable xij is defined as whether the person i is assigned to the task j. If so, xij = 1, and xij = 0 otherwise.
The concise-form formulation of the problem is as follows [3]:
Maximize:
Subject to:
The first constraint captures the requirement of assigning each person to a single task. The second constraint indicates that each task must be done by exactly one person. The objective function sums up the overall benefits of all assignments.
To see the analogy between the assignment problem and the network flow, we can describe each person supplying a flow of 1 unit and each task demanding a flow of 1 unit, with the benefits over all “channels” being maximized. [3]
A potential issue lies in the branching of the network, specifically an instance where a person splits their one unit of flow into multiple tasks and the objective remains maximized. This shortcoming is allowed by the laws that govern the network flow model, but are unfeasible in real-life instances. Fortunately, since the network simplex method only involves addition and subtraction of a single edge while transferring the basis, which is served by the spanning tree of the flow graph, if the supply (the number of people here) and the demand (the number of tasks here) in the constraints are integers, the solved variables will be automatically integers even if it is not explicitly stated in the problem. This is called the integrality of the network problem, and it certainly applies to the assignment problem. [6]
The Shortest-Path Problem
The shortest-path problem can be defined as finding the path that yields the shortest total distance between the origin and the destination. Each possible stop is a node and the paths between these nodes are edges incident to these nodes, where the path distance becomes the weight of the edges. In addition to being the most common and straightforward application for finding the shortest path, this model is also used in various applications depending on the definition of nodes and edges. [3] For example, when each node represents a different object and the edge specifies the cost of replacement, the equipment replacement problem is derived. Moreover, when each node represents a different project and the edge specifies the relative priority, the model becomes a project scheduling problem.
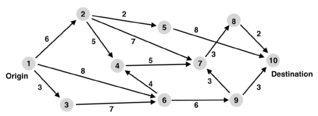
A graph of the general shortest-path problem is depicted as Figure 2:
In the general form of the shortest-path problem, the variable xij represents whether the edge (i, j) is active (i.e. with a positive flow), and the parameter cij (e.g. c12 = 6) defines the distance of the edge (i, j). The general problem is formulated as below:
Minimize
Subject to:
The first term of the constraint is the total outflow of the node i, and the second term is the total inflow. So, the formulation above could be seen as one unit of flow being supplied by the origin, one unit of flow being demanded by the destination, and no net inflow or outflow at any intermediate nodes. These constraints mandate a flow of one unit, amounting to the active path, from the origin to the destination. Under this constraint, the objective function minimizes the overall path distance from the origin to the destination.
Similarly, the integrality of the network problem applies here, precluding the unreasonable fractioning. With supply and demand both being integer (one here), the edges can only have integer amount of flow in the result solved by simplex method. [6]
In addition, the point-to-point model above can be further extended to other problems. A number of real life scenarios require visiting multiple places from a single starting point. This “Tree Problem” can be modeled by making small adjustments to the original model. In this case, the source node should supply more units of flow and there will be multiple sink nodes demanding one unit of flow. Overall, the objective and the constraint formulation are similar. [4]
Reference
4. Practical Optimization: A Gentle Introduction, Chapter 10 Network Flow Programming, John W. Chinneck, 2017.
5. Formulation and Analysis of Linear Programs, Chapter 5 Network Flows, Benjamin Van Roy and Kahn Mason, September 26, 2005. 6. Vanderbei, R. J. Network Problem (chapter 14). In R. J. Vanderbei (Ed.), Linear programming: Foundations and extensions. Boston: Springer, 2008.

![{\displaystyle \sum _{j=1}^{n}x_{ij}=1~~\forall i\in [1,n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d46325a2b6e76d35c51d81ceef2fa91f2aca545)
![{\displaystyle \sum _{I=1}^{n}x_{ij}=1~~\forall j\in [1,n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9de3c5cdb1695618c8f37553143205b7a27b04ae)
![{\displaystyle x_{ij}=0~or~1~~\forall i,j\in [0,n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/313acaeb7ffce1cada355b09f6cb2e23c3494931)

