Optimization with absolute values: Difference between revisions
Yilian Yin (talk | contribs) |
(Completed section on Absolute Values in Objective Functions and updated reference section.) |
||
| Line 22: | Line 22: | ||
In this case, the only solution is if <math>|X| = 0 </math>, simplifying the constraint to <math>X = 0 </math>. Note that this solution also occurs if the constraint is in the form <math>|X| <= 0 </math> due to the same conclusion (only solution <math>X = 0 </math>). | In this case, the only solution is if <math>|X| = 0 </math>, simplifying the constraint to <math>X = 0 </math>. Note that this solution also occurs if the constraint is in the form <math>|X| <= 0 </math> due to the same conclusion (only solution <math>X = 0 </math>). | ||
The second form a linear constraint can exist in is <math>|X| \le C </math> where <math display="inline">X </math> remains a linear combination of variables and constant <math display="inline">C > 0 </math>. | |||
In this case, we can describe an equivalent feasible solution by splitting the inequality into | In this case, we can describe an equivalent feasible solution by splitting the inequality into | ||
| Line 34: | Line 33: | ||
</math> and <math display="inline">C </math>, as shown below: | </math> and <math display="inline">C </math>, as shown below: | ||
[[File:Number Line X Less Than C.png|none|thumb]] | [[File:Number Line X Less Than C.png|none|thumb]] | ||
The last case for linear constraints is when <math>|X| \ge C </math>. | The last case for linear constraints is when <math>|X| \ge C </math>. | ||
| Line 40: | Line 38: | ||
Visually, the solution space is the complement of the second solution above, resulting in the following representation: | Visually, the solution space is the complement of the second solution above, resulting in the following representation: | ||
[[File:Number Line for X Greater Than C.png|none|thumb]] | [[File:Number Line for X Greater Than C.png|none|thumb]] | ||
In expression form, the solutions can be written as: | In expression form, the solutions can be written as: | ||
| Line 51: | Line 48: | ||
=== Absolute Values in Objective Functions === | === Absolute Values in Objective Functions === | ||
In objective functions, to leverage transformations of absolute functions, several conditions must be fulfilled: | |||
# First, the constraints must all be linear. | |||
# Secondly, the coefficient signs of the absolute terms must all be: | |||
#* Positive for a minimization problem | |||
#* Negative for a maximization problem | |||
At a high level, the transformation works similarly to the second case of absolute value in constraints – we aim to bound the solution space for the absolute value term with a new variable, <math display="inline">Y </math>. | |||
If <math>|X| </math> is the absolute value term in our objective function, where <math display="inline">X </math> is a linear combination of variables, | |||
Two additional constraints are added to the linear program: | |||
<math>X \le Y </math> | |||
<math>-X \le Y </math> | |||
This is a relaxation of the original function into a collection of linear constraints. | |||
In order to transform problems where the coefficient signs of the absolute terms do not fulfill the conditions above, a similar conclusion is reached to that of the last case for absolute values in constraints – the use of integer variables is needed to reach an LP format. | |||
==Numerical Example== | ==Numerical Example== | ||
| Line 169: | Line 185: | ||
== References == | == References == | ||
# "Absolute Values." ''lp_solve'', http://lpsolve.sourceforge.net/5.1/absolute.htm. Accessed 20 Nov. 2020. | |||
# ''Optimization Methods in Management Science / Operations Research.'' Massachusetts Institute of Technology, Spring 2013, https://ocw.mit.edu/courses/sloan-school-of-management/15-053-optimization-methods-in-management-science-spring-2013/tutorials/MIT15_053S13_tut04.pdf. Accessed 20 Nov. 2020. | |||
# http://lpsolve.sourceforge.net/5.1/absolute.htm | |||
# https://ocw.mit.edu/courses/sloan-school-of-management/15-053-optimization-methods-in-management-science-spring-2013/tutorials/MIT15_053S13_tut04.pdf | |||
# https://www.ise.ncsu.edu/fuzzy-neural/wp-content/uploads/sites/9/2019/08/LP-Abs-Value.pdf | # https://www.ise.ncsu.edu/fuzzy-neural/wp-content/uploads/sites/9/2019/08/LP-Abs-Value.pdf | ||
# Vanderbei R.J. (2008) Financial Applications. In: Linear Programming. International Series in Operations Research & Management Science, vol 114. Springer, Boston, MA. <nowiki>https://doi.org/10.1007/978-0-387-74388-2_13</nowiki> | # Vanderbei R.J. (2008) Financial Applications. In: Linear Programming. International Series in Operations Research & Management Science, vol 114. Springer, Boston, MA. <nowiki>https://doi.org/10.1007/978-0-387-74388-2_13</nowiki> | ||
Revision as of 01:06, 23 November 2020
Authors: Matthew Chan (mdc297), Yilian Yin (), Brian Amado (ba392), Peter (pmw99), Dewei Xiao (dx58) - SYSEN 5800 Fall 2020
Steward: Fengqi You
Introduction
Absolute values can make it relatively difficult to to determine the optimal solution when handled without first converting to standard form. This conversion of the objective function is a good first step in solving optimization problems with absolute values. As a result, you can go on to solve the problem using linear programing techniques.
Method
Defining Absolute Values
An absolute value of a real number can be described as its distance away from zero, or the non-negative magnitude of the number. Thus,
Absolute values can exist in optimization problems in two primary instances: in constraints and in the objective function.
Absolute Values in Constraints
Within linear equations, linear constraints can exist in several forms.
The first form exists as , where is a linear combination of variables.
In this case, the only solution is if , simplifying the constraint to . Note that this solution also occurs if the constraint is in the form due to the same conclusion (only solution ).
The second form a linear constraint can exist in is where remains a linear combination of variables and constant .
In this case, we can describe an equivalent feasible solution by splitting the inequality into
We can understand this visually as the solution must lie between and , as shown below:
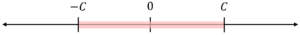
The last case for linear constraints is when .
Visually, the solution space is the complement of the second solution above, resulting in the following representation:
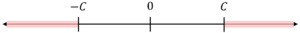
In expression form, the solutions can be written as:
As seen visually, the feasible region has a gap and thus non-convex. The expressions also make it impossible for both to simultaneously hold true. This means that it is not possible to transform constraints in this form to linear equations. An approach to reach a solution for this particular case exists in the form of Mixed-Integer Linear Programming, where only one of the equations above is “active”.
Absolute Values in Objective Functions
In objective functions, to leverage transformations of absolute functions, several conditions must be fulfilled:
- First, the constraints must all be linear.
- Secondly, the coefficient signs of the absolute terms must all be:
- Positive for a minimization problem
- Negative for a maximization problem
At a high level, the transformation works similarly to the second case of absolute value in constraints – we aim to bound the solution space for the absolute value term with a new variable, .
If is the absolute value term in our objective function, where is a linear combination of variables,
Two additional constraints are added to the linear program:
This is a relaxation of the original function into a collection of linear constraints.
In order to transform problems where the coefficient signs of the absolute terms do not fulfill the conditions above, a similar conclusion is reached to that of the last case for absolute values in constraints – the use of integer variables is needed to reach an LP format.
Numerical Example
We replace the absolute value quantities with a single variable:
We must introduce additional constraints to ensure we do not lose any information by doing this substitution:
The problem has now been reformulated as a linear programming problem that can be solved normally:
The optimum value for the objective function is , which occurs when and and .
Applications
There are no specific applications to Optimization with Absolute Values however it is necessary to account for at times when utilizing the simplex method.
Consider the problem Ax=b; max z= x c,jx,i. This problem cannot, in general, be solved with the simplex method. The problem has a simplex method solution (with unrestricted basis entry) only if c, are nonpositive (non-negative for minimizing problems).
The primary application of absolute-value functionals in linear programming has been for absolute-value or L(i)-metric regression analysis. Such application is always a minimization problem with all C(j) equal to 1 so that the required conditions for valid use of the simplex method are met.
By reformulating the original problem into a Mixed-Integer Linear Program (MILP), in most case we should be able to use GAMS/Pyomo/JuliaOPT to solve the problem.
WIP
3
- Application in Financial: Portfolio Selection
Under this topic, we are going to use the same tricks we played in the Numerical Example section to perform Reduction to a Linear Programming Problem, to reform the problem into a MILP, in order to solve the problem. Let's have a look of the example.
A portfolio is determined by what fraction of one's assets to put into each investment. It can be denoted as a collection of nonnegative numbers xj, where j = 1, 2,...,n. Because each xj stands for a portion of the assets, it sums to one. In order to get a highest reward through finding a right mix of assets, let , the positive parameter, denote the importance of risk relative to the return, and Rj denote the return in the next time period on investment j, j = 1, 2,..., n. The total return one would obtain from the investment is . The expected return is . And the Mean Absolute Deviation from the Mean (MAD) is .
maximize
subject to
where
Very obviously, this problem is not a linear programming problem yet. So we have to use the same trick we used in the numeric example, to replace each absolute value with a new variable and impose inequality constraints to ensure that the new variable is the appropriate absolute value once an optimal value is obtained. To simplify the program, we decide to take the average of the historical returns in order to get the mean expected return: . Thus the objective function turns into:
Now, replace with a new variable and thus the problem can be rewrote as:
maximize
subject to . t = 1, 2,...,T
where
. j = 1, 2,...,n
. t = 1, 2,...,T
So finally, after some simplifications methods and some tricks applied, the original problem is converted into a linear programming which is easier to be solved further.
Let's see some other applications:
- Minimizing the sum of absolute deviations
- Minimizing the maximum of absolute values
Conclusion
The presence of an absolute value within the objective function prevents the use of certain optimization methods. Solving these problems requires that the function be manipulated in order to continue with linear programming techniques like the simplex method.
References
- "Absolute Values." lp_solve, http://lpsolve.sourceforge.net/5.1/absolute.htm. Accessed 20 Nov. 2020.
- Optimization Methods in Management Science / Operations Research. Massachusetts Institute of Technology, Spring 2013, https://ocw.mit.edu/courses/sloan-school-of-management/15-053-optimization-methods-in-management-science-spring-2013/tutorials/MIT15_053S13_tut04.pdf. Accessed 20 Nov. 2020.
- https://www.ise.ncsu.edu/fuzzy-neural/wp-content/uploads/sites/9/2019/08/LP-Abs-Value.pdf
- Vanderbei R.J. (2008) Financial Applications. In: Linear Programming. International Series in Operations Research & Management Science, vol 114. Springer, Boston, MA. https://doi.org/10.1007/978-0-387-74388-2_13














































