Optimization with absolute values
Authors: Matthew Chan (mdc297), Yilian Yin (), Brian Amado (ba392), Peter (pmw99), Dewei Xiao (dx58) - SYSEN 5800 Fall 2020
Steward: Fengqi You
Method
Defining Absolute Values
An absolute value of a real number can be described as its distance away from zero, or the non-negative magnitude of the number. Thus,
Absolute values can exist in optimization problems in two primary instances: in constraints and in the objective function.
Absolute Values in Constraints
Within linear equations, linear constraints can exist in several forms.
The first form exists as , where is a linear combination of variables.
In this case, the only solution is if , simplifying the constraint to . Note that this solution also occurs if the constraint is in the form due to the same conclusion (only solution ).
Second form a linear constraint can exist in is where remains a linear combination of variables and constant .
In this case, we can describe an equivalent feasible solution by splitting the inequality into
We can understand this visually as the solution must lie between and , as shown below:
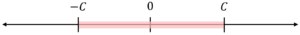
The last case for linear constraints is when .
Visually, the solution space is the complement of the second solution above, resulting in the following representation:
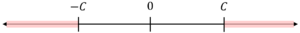
In expression form, the solutions can be written as:
As seen visually, the feasible region has a gap and thus non-convex. The expressions also make it impossible for both to simultaneously hold true. This means that it is not possible to transform constraints in this form to linear equations. An approach to reach a solution for this particular case exists in the form of Mixed-Integer Linear Programming, where only one of the equations above is “active”.
Absolute Values in Objective Functions
WIP
Numerical Example
We replace the absolute value quantities with a single variable:
We must introduce additional constraints to ensure we do not lose any information by doing this substitution:
The problem has now been reformulated as a linear programming problem that can be solved normally:
The optimum value for the objective function is , which occurs when and and .
References
To be formatted:


























