Quadratic assignment problem: Difference between revisions
| Line 9: | Line 9: | ||
== Example == | == Example == | ||
Consider the QAP of placing <math>i=3</math> | Consider the QAP of placing 3 facilities in 3 locations. Let the distance and flow matrices be defined respectively as <math>D_{i,j}=\begin{bmatrix} 0 & 5 & 6 \\ 5 & 0 & 3.6 \\ 6 & 3.6 & 0 \end{bmatrix} | ||
</math>, <math display="inline">F_{i,j}=\begin{bmatrix} 0 & 10 & 3 \\ 10 & 0 & 6.5\\ 3 & 6.5 & 0 \end{bmatrix} | |||
</math>. For each pair <math>(i,j)</math>, <math>D_{i,j}</math> represents the distance between locations <math>i</math> and <math>j</math>. <math>F_{i,j}</math> represents the required flow between facilities <math>i</math> and <math>j</math>. The optimal solution will be the arrangement of the 3 facilities in the 3 locations so that the total flow over distance is minimized. Intuitively, this means the facilities with the highest flow between them are closer together to minimize costs, time, etc. going between the two facilities. | |||
There are <math>3! = 6</math> permutations of the 3 facilities in the 3 locations. The set of these permutations is typically denoted <math>S_3 </math> The permutation <math>\phi=(3 2 1)</math> represents facility 3 being placed at location 1, facility 1 at location 2 and facility 2 at location 3. Each permutation can be assigned a permutation matrix. The permutation matrix of <math>\phi = \begin{bmatrix} x & y & c \\ z & v &c \\ a &v & c\end{bmatrix}</math> | |||
== Applications == | == Applications == | ||
Revision as of 17:59, 21 November 2020
Author: Thomas Kueny, Eric Miller, Natasha Rice, Joseph Szczerba, David Wittmann (SysEn 5800 Fall 2020)
Introduction
Theory, Methodology, and/or Algorithmic Discussions
Joe Szczerba and Tom Kueny to provide.
Example
Consider the QAP of placing 3 facilities in 3 locations. Let the distance and flow matrices be defined respectively as , . For each pair , represents the distance between locations and . represents the required flow between facilities and . The optimal solution will be the arrangement of the 3 facilities in the 3 locations so that the total flow over distance is minimized. Intuitively, this means the facilities with the highest flow between them are closer together to minimize costs, time, etc. going between the two facilities.
There are permutations of the 3 facilities in the 3 locations. The set of these permutations is typically denoted The permutation represents facility 3 being placed at location 1, facility 1 at location 2 and facility 2 at location 3. Each permutation can be assigned a permutation matrix. The permutation matrix of
Applications
Natasha Rice and David Wittmann to provide.
The Backboard Wiring Problem
As the quadratic assignment problem is focused on minimizing the cost of traveling from one location to another, it is an ideal approach determining placement of components in many modern electronics. Leon Steinberg proposed a QAP solution optimize the layout of elements on a blackboard by minimizing the total amount of wiring required.
When defining the problem Steinberg states that we have a set of n elements
as well as a set of r points
where
In his paper he derives the below formula:
represents the number of wires connecting components and
is the length of wire needed to connect tow components if one is placed at and the other is placed at . If has coordinates then can be calculated by
represents a particular placement of a component.
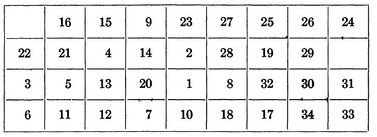
In his paper Steinberg a backboard with a 9 by 4 array, allowing for 36 potential positions for the 34 components that needed to be placed on the backboard. For the calculation he selected a random initial placement of s1 and chose a random family of 25 unconnected sets.
The initial placement of components is shown below:

After the initial placement of elements it took an additional 35 iterations to get us to our final optimized backboard layout. Leading to a total of 59 iterations and a final wire length of 4,969.440.
Hospital Layout
Campus Building Arrangement
Molecular Confrontation Problem
Conclusion
References
- Alwalid N. Elshafei. Hospital Layout as a Quadratic Assignment Problem. Operational Research Quarterly (1970-1977). 1977;28(1):167. doi:10.2307/3008789
- Dickey JW, Hopkins JW. Campus building arrangement using topaz. Transportation Research. 6(1):59-68. doi:10.1016/0041-1647(72)90111-6
- Leon Steinberg. The Backboard Wiring Problem: A Placement Algorithm. SIAM Review. 1961;3(1):37.
- Phillips AT, Rosen JB. A quadratic assignment formulation of the molecular conformation problem. Journal of Global Optimization: An International Journal Dealing with Theoretical and Computational Aspects of Seeking Global Optima and Their Applications in Science, Management, and Engineer. 1994;4(2):229. doi:10.1007/bf01096724
- https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.217.1914&rep=rep1&type=pdf






















