Quadratic assignment problem: Difference between revisions
m (→Inner Product) |
|||
| Line 34: | Line 34: | ||
The inner product of two matrices <math>A,B</math> is defined as <math><A,B> = \sum_{i=1}^{n}\sum_{j=1}^{n}a_{i,j}b_{i,j}</math>. The inner product <math><F,X_{\phi}DX_{\phi}^{T}> = \sum_{i=1}^{n}\sum_{j=1}^{n}F_{i,j}(X_{\phi}DX_{\phi}^{T})_{i,j}</math> thus describes the total cost of assigning facilities <ref name="psu" /> to locations according to <math>\phi</math>. The objective function to minimize cost can be written as <math><F,XDX^{T}></math>. | The inner product of two matrices <math>A,B</math> is defined as <math><A,B> = \sum_{i=1}^{n}\sum_{j=1}^{n}a_{i,j}b_{i,j}</math>. The inner product <math><F,X_{\phi}DX_{\phi}^{T}> = \sum_{i=1}^{n}\sum_{j=1}^{n}F_{i,j}(X_{\phi}DX_{\phi}^{T})_{i,j}</math> thus describes the total cost of assigning facilities <ref name="psu" /> to locations according to <math>\phi</math>. The objective function to minimize cost can be written as <math><F,XDX^{T}></math>. | ||
The true objective cost function only uses the entries above the diagonal in the matrix comprised of elements <math>F_{i,j}</math><math>(X_{\phi}DX_{\phi}^{T})_{i,j} </math>.Since this matrix is symmetric with zeroes on the diagonal, dividing by 2 removes the double count of each element to give the correct cost value. | |||
The true objective cost function only uses the entries above the diagonal in the matrix comprised of elements <math>F_{i,j}</math><math>(X_{\phi}DX_{\phi}^{T})_{i,j} </math>.Since this matrix is symmetric with zeroes on the diagonal, dividing by 2 removes the double count of each element to give the correct cost value. | |||
=== QAP with 3 Facilities === | === QAP with 3 Facilities === | ||
Revision as of 21:27, 24 November 2020
Author: Thomas Kueny, Eric Miller, Natasha Rice, Joseph Szczerba, David Wittmann (SysEn 5800 Fall 2020)
Introduction
The Quadratic Assignment Problem, discovered by Koopmans and Beckmann in 1957, is a mathematical optimization module created to describe the location of invisible economic activities. An NP Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize backboards, Inter-plant Transportation, Hospital Transportation, Exam Scheduling, along with many other applications not described within this page.
Theory, Methodology, and/or Algorithmic Discussions
Computational Complexity
QAP belongs to the classification of problems known as NP-complete, thus being a computationally complex problem. QAP’s NP-completeness was proven by Sahni and Gonzalez in 1976, who state that of all combinatorial optimization problems, QAP is the “hardest of the hard”.[1]
Algorithmic Discussions
While an algorithm that can solve QAP in polynomial time is unlikely to exist, there are three primary methods for acquiring the optimal solution to a QAP problem:
- Dynamic Program
- Cutting Plane
- Branch and Bound Procedures
The third method has been proven to be the most effective in solving QAP, although when n > 15, QAP begins to become virtually unsolvable.
Numerical Example
Distance and Flow Matrices
For each pair , represents the distance between locations and . represents the required flow (of supplies, products, etc.) between facilities and [2]. The optimal solution will be the arrangement of the 3 facilities in the 3 locations so that the total flow over distance is minimized. Intuitively, the product of distance and flow represents cost, and the objective is to minimize this cost. Ideally, two facilities with lots of flow (more product or supplies) between the two should be placed closer together than two facilities that rarely interact (low flow).
Permutations
There are permutations of the 3 facilities in the 3 locations. The set of these permutations is typically denoted . As an example, the permutation represents facility 3 being placed at location 1, facility 1 at location 2 and facility 2 at location 3. Each permutation can be assigned a permutation matrix. The permutation matrix of can be written as [3]
The operation permutes the values of the distance matrix so that represents the distance between facilities and if the facilities are arranged according to the permutation . The cost function between facilities and , after being permuted to their location, is [3]. To find the total cost, sum over each and for the facilities arranged according to .
Inner Product
The inner product of two matrices is defined as . The inner product thus describes the total cost of assigning facilities [3] to locations according to . The objective function to minimize cost can be written as .
The true objective cost function only uses the entries above the diagonal in the matrix comprised of elements .Since this matrix is symmetric with zeroes on the diagonal, dividing by 2 removes the double count of each element to give the correct cost value.
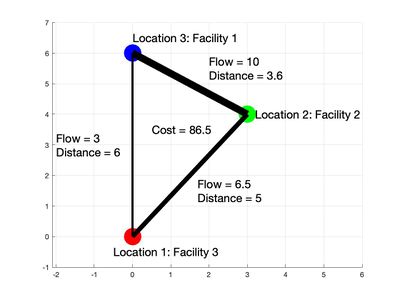
QAP with 3 Facilities
Consider the QAP of placing 3 facilities in 3 locations. Let the distance and flow matrices be defined respectively as , .
Let be the set of permutation matrices for . The problem can be stated as follows:
.
The table lists the resulting cost function to place the facilities according to each permutation . Note that is the identity mapping where the number of the facility is the location number. Based on these results, is the arrangement of facilities that minimizes the cost function with a value of 86.5. Facility 1 should be placed at location 3, Facility 2 remains at location 2 and Facility 3 is placed at location 1.
| Permutation | Cost |
| ( ) | 91.4 |
| 99.8 | |
| 98.4 | |
| 86.5 | |
| 103.3 | |
| 90 |
Applications
Inter-plant Transportation Problem
The quadratic assignment problem was first introduced by Koopmans and Beckmann to address how economic decisions could be made to optimize the transportation costs of goods between both manufacturing plants and locations.[4] Factoring in the location of the each of the manufacturing plants as well as the volume of goods between locations to maximize revenue is what distinguishes this from other linear programming assignment problems like the Knapsack Problem.
The Backboard Wiring Problem
As the quadratic assignment problem is focused on minimizing the cost of traveling from one location to another, it is an ideal approach determining placement of components in many modern electronics. Leon Steinberg proposed a QAP solution optimize the layout of elements on a blackboard by minimizing the total amount of wiring required.[5]
When defining the problem Steinberg states that we have a set of n elements
as well as a set of r points
where
In his paper he derives the below formula:
represents the number of wires connecting components and
is the length of wire needed to connect tow components if one is placed at and the other is placed at . If has coordinates then can be calculated by
represents a particular placement of a component.
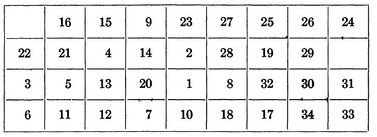
In his paper Steinberg a backboard with a 9 by 4 array, allowing for 36 potential positions for the 34 components that needed to be placed on the backboard. For the calculation he selected a random initial placement of s1 and chose a random family of 25 unconnected sets.
The initial placement of components is shown below:

After the initial placement of elements it took an additional 35 iterations to get us to our final optimized backboard layout. Leading to a total of 59 iterations and a final wire length of 4,969.440.
Hospital Layout
Building a new hospitals was a common event in 1977 when Alealid N Elshafei wrote his paper on "Hospital Layouts as a Quadratic Assignment Problem".[6]With high initial cost to construct the hospital and to staff it, it is important to ensure that it is operating as efficiently as possible. Elshafei's paper was commissioned to create a optimization formula to locate clinics within a building in such a way that minimizes the total distance that a patient travels within the hospital throughout the year. When doing a study of a major hospital in Cairo he determined that the Out-patient ward was acting as a bottle neck in the hospital and focused his efforts on optimizing the 17 departments there.
Elshafei identified the following QAP to determine where clinics should be placed:
Such that
is the yearly flow between facilities i and k
is the distance between the possible facility locations j and q
is the initial set of facilities
is the initial set of all locations
It can take a large amount of computational power to calculate the solution to a QAP problem, necessitating the use of a heuristic solution rather than using an optimizing algorithm. This approach is composed of two parts(Parts A and Part B). Part A that develops the initial layout of the hospital, this is done by following two strategies. Strategy 1 where we use a rank that designates the number of interactions facility has with with the other facilities. As well as ranking them in terms of , which designates the sum of distances from j to all other locations. then we go through the list and find the facility with the greatest and the least . Strategy 2 says that any step in the process we next place an unassigned facility that has the largest number of interactions with the most recently placed facility. Part B covers improving the initial solution developed in Part A, here at any step in the process we test weather the assignment is best of all of the facilities that are involved and make swaps where necessary until there are no more swaps to be made.
For the Cairo hospital with 17 clinics, and one receiving and recording room bringing us to a total of 18 facilities. By running the above optimization Elshafei was able to get the total distance per year down to 11,281,887 from a distance of 13,973,298 biased on the original hospital layout.
Exam Scheduling System
The scheduling system uses matrices for Exams, Time Slots, and Rooms with the goal of reducing the rate of schedule conflicts. To accomplish this goal, the “examination with the highest cross faculty student is been prioritized in the schedule after which the examination with the highest number of cross program is considered and finally with the highest number of repeating student, at each stage group with the highest number of student are prioritized.”[7]
Conclusion
References
- ↑ Burkard R.E., Çela E., Pardalos P.M., Pitsoulis L.S. (1998) The Quadratic Assignment Problem. In: Du DZ., Pardalos P.M. (eds) Handbook of Combinatorial Optimization. Springer, Boston, MA. https://doi.org/10.1007/978-1-4613-0303-9_27
- ↑ https://neos-guide.org/content/quadratic-assignment-problem
- ↑ 3.0 3.1 3.2 https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.217.1914&rep=rep1&type=pdf
- ↑ Koopmans, T., & Beckmann, M. (1957). Assignment Problems and the Location of Economic Activities. Econometrica, 25(1), 53-76. doi:10.2307/1907742
- ↑ Leon Steinberg. The Backboard Wiring Problem: A Placement Algorithm. SIAM Review. 1961;3(1):37.
- ↑ Alwalid N. Elshafei. Hospital Layout as a Quadratic Assignment Problem. Operational Research Quarterly (1970-1977). 1977;28(1):167. doi:10.2307/300878
- ↑ Muktar, D., & Ahmad, Z.M. (2014). Examination Scheduling System Based On Quadratic Assignment.

















































