RMSProp: Difference between revisions
Jason Huang (talk | contribs) No edit summary |
Jason Huang (talk | contribs) No edit summary |
||
| Line 15: | Line 15: | ||
Artificial Neural Network can be regarded as the human brain and conscious center of Aritifical Intelligence(AI), presenting the imitation of what the mind will be when human thinking. Scientists are trying to build the concept of ANN close real neurons with their biological ‘parent’. | Artificial Neural Network can be regarded as the human brain and conscious center of Aritifical Intelligence(AI), presenting the imitation of what the mind will be when human thinking. Scientists are trying to build the concept of ANN close real neurons with their biological ‘parent’. | ||
[[File:Neuron.png|thumb|A single neuron presented as a mathematic function ]]And the function of neurons can be presented as: | [[File:Neuron.png|thumb|A single neuron presented as a mathematic function ]]And the function of neurons can be presented as: | ||
<math>f (x_{1},x_{2}) = max(0, w_{1} x_{1} + w_{2} x_{2}) </math> | <math>f (x_{1},x_{2}) = max(0, w_{1} x_{1} + w_{2} x_{2}) </math> | ||
| Line 25: | Line 27: | ||
RProp, or we call Resilient Back Propagation, is the widely used algorithm for supervised learning with multi-layered feed-forward networks in the past. Besides, its concepts is the foundation of RMSPRop development t. The derivatives equation of error function can be represented as: | RProp, or we call Resilient Back Propagation, is the widely used algorithm for supervised learning with multi-layered feed-forward networks in the past. Besides, its concepts is the foundation of RMSPRop development t. The derivatives equation of error function can be represented as: | ||
<math> \frac{\partial E}{\partial w_{ij}} = \frac{\partial E}{\partial s_{i}} \frac{\partial s_{i}}{\partial net_{i}} \frac{\partial net_{i}}{\partial w_{ij}}</math> | <math> \frac{\partial E}{\partial w_{ij}} = \frac{\partial E}{\partial s_{i}} \frac{\partial s_{i}}{\partial net_{i}} \frac{\partial net_{i}}{\partial w_{ij}}</math> | ||
Where <math>w_{ij}</math> is the weight from neuron <math>j</math> to neuron <math>i</math>, <math>s_{i}</math> is the output , and <math>net_{i}</math> is the weighted sum of the inputs of neurons <math>i</math>. Once the weight of each partial derivatives is known, the error function can be presented by performing a simple gradient descent: | Where <math>w_{ij}</math> is the weight from neuron <math>j</math> to neuron <math>i</math>, <math>s_{i}</math> is the output , and <math>net_{i}</math> is the weighted sum of the inputs of neurons <math>i</math>. Once the weight of each partial derivatives is known, the error function can be presented by performing a simple gradient descent: | ||
| Line 44: | Line 46: | ||
However, It turns out that the optimal value of the momentum parameter <math>\mu</math> is equally problem dependent as the learning rate <math>\epsilon</math>, and that no general improvement can be accomplished. Besides, RProp algorithm is not function well when we have very large datasets and need to perform mini-batch weights updates. | However, It turns out that the optimal value of the momentum parameter <math>\mu</math> is equally problem dependent as the learning rate <math>\epsilon</math>, and that no general improvement can be accomplished. Besides, RProp algorithm is not function well when we have very large datasets and need to perform mini-batch weights updates. | ||
| Line 64: | Line 67: | ||
==Numerical Example== | ==Numerical Example== | ||
| Line 72: | Line 76: | ||
For the specific package supporting RMSProp in python, refer to [https://www.programcreek.com/python/example/104283/keras.optimizers.RMSprop Python keras.optimizers.RMSprop() Examples] for both 3D and 2D implementation. | For the specific package supporting RMSProp in python, refer to [https://www.programcreek.com/python/example/104283/keras.optimizers.RMSprop Python keras.optimizers.RMSprop() Examples] for both 3D and 2D implementation. | ||
== Applicants == | == Applicants and Discussion == | ||
[[File:1 - 2dKCQHh - Long Valley.gif|thumb|Visualizing Optimization algorithm comparing convergence with similar algorithm<sup>1</sup>]] | |||
gradients based optimization algorithm has different convergence rate. As the visualizations shown, the without scaling based on gradient information algorithms are hard to break the symmetry and converge rapidly. RMSProp has a relative converge rate than others, but it is not the fastest one. | |||
Revision as of 08:22, 19 November 2020
Author: Jason Huang (SysEn 6800 Fall 2020)
Steward: Allen Yang, Fengqi You
Introduction
RMSProp, so call root mean square propagation, is an optimization algorithm/method dealing with Artificial Neural Network (ANN) for machine learning. It is also a currently developed algorithm compared to the Stochastic Gradient Descent (SGD) algorithm, momentum method. And even one of the foundations of Adam algorithm development. It is an unpublished optimization algorithm, using the adaptive learning rate method, first proposed in the Coursera course “Neural Network for Machine Learning” lecture six by Geoff Hinton. Astonished is that this informally revealed, an unpublished algorithm is intensely famous nowadays.
Theory and Methodology
Artificial Neural Network
Artificial Neural Network can be regarded as the human brain and conscious center of Aritifical Intelligence(AI), presenting the imitation of what the mind will be when human thinking. Scientists are trying to build the concept of ANN close real neurons with their biological ‘parent’.
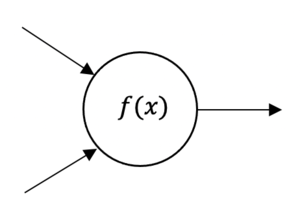
And the function of neurons can be presented as:
Where are two inputs numbers, and function will takes these fixed inputs and create an output of single number. If is greater than 0, the function will return this positive value, or return 0 otherwise. Therefore, the neural network can be replaced as a coupled mathematical function, and its output of a previous function can be used as the next function input.
RProp
RProp, or we call Resilient Back Propagation, is the widely used algorithm for supervised learning with multi-layered feed-forward networks in the past. Besides, its concepts is the foundation of RMSPRop development t. The derivatives equation of error function can be represented as:
Where is the weight from neuron to neuron , is the output , and is the weighted sum of the inputs of neurons . Once the weight of each partial derivatives is known, the error function can be presented by performing a simple gradient descent:
(reference required)
Obviously, the choice of the learning rate , which scales the derivative, has an important effect on the time needed until convergence is reached. If it is set too small, too many steps are needed to reach an acceptable solution; on the contrary a large learning rate will possibly lead to oscillation, preventing the error to fall below a certain value.
In addition, RProp can combine the method with momentum method, to prevent above problem and to accelerate the convergence rate, the equation can rewrite as:
However, It turns out that the optimal value of the momentum parameter is equally problem dependent as the learning rate , and that no general improvement can be accomplished. Besides, RProp algorithm is not function well when we have very large datasets and need to perform mini-batch weights updates.
RMSProp
RProp algorithm doesn’t work for mini-batches is that it violates the central idea behind stochastic gradient descent, which is when we have small enough learning rate, it averages the gradients over successive mini-batches. To solve this issue, consider the weight, that gets the gradient 0.1 on nine mini-batches, and the gradient of -0.9 on tenths mini-batch, RMSProp did force those gradients to roughly cancel each other out, so that the stay approximately the same.
By using the sign of gradient from RProp algorithm, and the mini-batches efficiency, and averaging over mini-batches which allows to combine gradients in the right way. PMSProp is keep the moving average of the squared gradients for each weight. And then we divide the gradient by square root the mean square.
The updated equation can be performed as:
where is the moving average of squared gradients, is gradient of the cost function with respect to the weight, is the learning rate and is moving average parameter (default value — 0.9).
The equation adapt the learning rate by dividing by the squared gradients, However, since we only have the estimate of the gradient on the current mini-batch, we need instead to use the moving average, which is set as default 0.9, of it.
Numerical Example
2D RMSProp Example
For the 2-Dimension of how RMSProp function, refer to "Dive into Deep Learning website". In the link, the implementation of function is well presented.
For the specific package supporting RMSProp in python, refer to Python keras.optimizers.RMSprop() Examples for both 3D and 2D implementation.
Applicants and Discussion
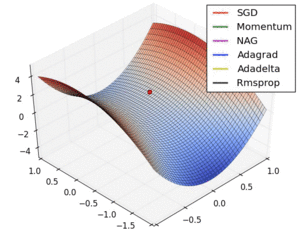
gradients based optimization algorithm has different convergence rate. As the visualizations shown, the without scaling based on gradient information algorithms are hard to break the symmetry and converge rapidly. RMSProp has a relative converge rate than others, but it is not the fastest one.














=\beta E[g^{2}](t-1)+(1-\beta )({\frac {\partial c}{\partial w}})^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b6799b3b78c1a1a89345c9ce27e3513a12d15ad)
![{\displaystyle w_{ij}(t)=w_{ij}(t-1)-{\frac {\eta }{\sqrt {E[g^{2}]}}}{\frac {\partial c}{\partial w_{ij}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1480ef765e74e5d3817b7ca131ea4a8ad5a9a93c)
![{\displaystyle E[g]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0c4d6ea8063c3234e530a440078ab4418dff5c0)



