Simplex algorithm: Difference between revisions
No edit summary |
Apoorv12345 (talk | contribs) No edit summary |
||
| (26 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
Author: Guoqing Hu (SysEn 6800 Fall 2020) | Author: Guoqing Hu (SysEn 6800 Fall 2020) | ||
== Introduction == | == Introduction == | ||
Simplex algorithm (or Simplex method) is a widely-used algorithm to solve the Linear Programming(LP). | Simplex algorithm (or Simplex method) is a widely-used algorithm to solve the Linear Programming(LP) optimization problems. The simplex algorithm can be thought of as one of the elementary steps for solving the inequality problem, since many of those will be converted to LP and solved via Simplex algorithm.<ref name=":0">[http://www-personal.umich.edu/~murty/books/linear_complementarity_webbook/lcp-complete.pdf Linear complementarity, linear and nonlinear programming Internet Edition].</ref> Simplex algorithm has been proposed by [[Wikipedia: George_Dantzig|George Dantzig]], initiated from the idea of step by step downgrade to one of the vertices on the convex polyhedral.<ref>Dantzig, G. B. (1987, May). [https://apps.dtic.mil/dtic/tr/fulltext/u2/a182708.pdf Origins of the simplex method].</ref> "Simplex" could be possibly referred to as the top vertex on the simplicial cone which is the geometric illustration of the constraints within LP problems.<ref>Strang, G. (1987). Karmarkar’s algorithm and its place in applied mathematics. ''The Mathematical Intelligencer,'' ''9''(2), 4-10. doi:10.1007/bf03025891.</ref> | ||
== Algorithmic Discussion | == Algorithmic Discussion == | ||
There are two | There are two theorems in LP: | ||
# The feasible region for | # The feasible region for an LP problem is a convex set (Every linear equation's second derivative is 0, implying the monotonicity of the trend). Therefore, if an LP has an optimal solution, there must be an extreme point of the feasible region that is optimal | ||
# For | # For an LP optimization problem, there is only one extreme point of the LP's feasible region regarding every basic feasible solution. Plus, there will be a minimum of one basic feasible solution corresponding to every extreme point in the feasible region.<ref name=":1">Vanderbei, R. J. (2000). ''Linear programming: Foundations and extensions''. Boston: Kluwer.</ref> | ||
[[File:Geometric Illustration of LP problem.png|thumb|Geometric Illustration of LP problem]] | [[File:Geometric Illustration of LP problem.png|thumb|Geometric Illustration of LP problem]] | ||
Based on two theorems above, the geometric illustration of the LP problem could be depicted. Each line of this polyhedral will be the boundary of the LP constraints, in which every vertex will be the extreme points according to the theorem. | Based on the two theorems above, the geometric illustration of the LP problem could be depicted. Each line of this polyhedral will be the boundary of the LP constraints, in which every vertex will be the extreme points according to the theorem. The simplex method is the way to adjust the nonbasic variables to travel to different vertex till the optimum solution is found.<ref>Sakarovitch M. (1983) Geometric Interpretation of the Simplex Method. In: Thomas J.B. (eds) Linear Programming. Springer Texts in Electrical Engineering. Springer, New York, NY. <nowiki>https://doi.org/10.1007/978-1-4757-4106-3_8</nowiki></ref> | ||
Consider the following expression as the general linear programming problem standard form: | Consider the following expression as the general linear programming problem standard form: | ||
| Line 26: | Line 24: | ||
The first step of the simplex method is to add slack variables and symbols which represent the objective functions: | The first step of the simplex method is to add slack variables and symbols which represent the objective functions: | ||
<math> \begin{align} \phi &= \sum_{i=1}^n | <math> \begin{align} \phi &= \sum_{i=1}^n c_ix_i\\ | ||
z_i &= b_i - \sum_{j=1}^n a_{ij}x_j \quad i = 1,2,...,m \end{align} </math> | z_i &= b_i - \sum_{j=1}^n a_{ij}x_j \quad i = 1,2,...,m \end{align} </math> | ||
The new introduced slack variables may be confused with the original values. Therefore, it will be convenient to add those slack variables to the end of the list of ''x''-variables with the following expression: | The new introduced slack variables may be confused with the original values. Therefore, it will be convenient to add those slack variables <math> z_i </math> to the end of the list of ''x''-variables with the following expression: | ||
<math> \begin{align} \phi &= \sum_{ | <math> \begin{align} \phi &= \sum_{i=1}^n c_ix_i\\ | ||
x_{n+i} &= b_i - \sum_{j=1}^n a_{ij}x_{ij} \quad i=1,2,...,m \end{align} </math> | x_{n+i} &= b_i - \sum_{j=1}^n a_{ij}x_{ij} \quad i=1,2,...,m \end{align} </math> | ||
| Line 37: | Line 35: | ||
<math> \begin{align} | <math> \begin{align} | ||
\phi &= \bar{\phi} + \sum_{j=1}^n \bar{ | \phi &= \bar{\phi} + \sum_{j=1}^n \bar{c_j}x_j\\ | ||
x_{ | x_{i} &= \bar{b_i} - \sum_{j=1}^n \bar{a_{ij}}x_{ij} \quad i=1,2,...,n+m | ||
\end{align} </math> | \end{align} </math> | ||
Where the variables with bar suggest that those corresponding values will change accordingly with the progression of simplex method. The observation could be made that there will specifically one variable goes from non-basic to basic and | Where the variables with bar suggest that those corresponding values will change accordingly with the progression of the simplex method. The observation could be made that there will specifically one variable goes from non-basic to basic and another acts oppositely. This kind of variable is referred to as the ''entering variable''. Under the goal of increasing <math>\phi</math>, the entering variables are selected from the set {1,2,...,n}. As long as there are no repetitive entering variables can be selected, the optimal values will be found. The decision of which entering variable should be selected at first place should be made based on the consideration that there usually are multiple constraints (n>1). For the Simplex algorithm, the coefficient with the least value is preferred since the major objective is maximization. | ||
The ''leaving variables'' are defined as which go from basic to non-basic. The reason of their existence is to ensure the non-negativity of those basic variables. Once the entering variables are determined, the corresponding leaving variables will change accordingly from the equation below: | The ''leaving variables'' are defined as which go from basic to non-basic. The reason of their existence is to ensure the non-negativity of those basic variables. Once the entering variables are determined, the corresponding leaving variables will change accordingly from the equation below: | ||
<math> x_i = \bar{b_i} - \bar{a_{ik}}x_k \quad i \, \epsilon \, \{ 1,2,...,n \}</math> | <math> x_i = \bar{b_i} - \bar{a_{ik}}x_k \quad i \, \epsilon \, \{ 1,2,...,n+m \}</math> | ||
Since the non-negativity of entering variables should be ensured, the following inequality can be derived: | Since the non-negativity of entering variables should be ensured, the following inequality can be derived: | ||
<math> \bar{b_i} - \bar{a_i}x_k \geq 0 \quad i\,\epsilon\, \{1,2,...,n\}</math> | <math> \bar{b_i} - \bar{a_i}x_k \geq 0 \quad i\,\epsilon\, \{1,2,...,n+m \}</math> | ||
Where | Where <math>x_k</math> is immutable. The minimum <math>x_i</math> should be zero to get the minimum value since this cannot be negative. Therefore, the following equation should be derived: | ||
<math> x_k = \frac {\bar{b_i}}{\bar{a_{ik}}} </math> | <math> x_k = \frac {\bar{b_i}}{\bar{a_{ik}}} </math> | ||
Due the nonnegativity of all variables, the value of | Due to the nonnegativity of all variables, the value of <math>x_k</math> should be raised to the largest of all of those values calculated from above equation. Hence, the following equation can be derived: | ||
<math> x_k = \min_{\bar{a_{ik}}>0} \, \frac{\bar{b_i}}{\bar{a_{ik}}} \quad i=1,2,...,n+m</math> | |||
Once the leaving-basic and entering-nonbasic variables are chosen, reasonable row operation should be conducted to switch from the current dictionary to the new dictionary, as this step is called ''pivot.''<ref name=":1" /> | |||
As in the pivot process, the coefficient for the selected pivot element should be one, meaning the reciprocal of this coefficient should be multiplied to every element within this row. Afterward, multiplying this specific row with corresponding coefficients and adding this to different rows, one should get 0 values for all other entries in this pivot element's column. | |||
If there are any negative variables after the pivot process, one should continue finding the pivot element by repeating the process above. At once there are no more negative values for basic and non-basic variables. The optimal solution is found.<ref>Evar D. Nering and Albert W. Tucker, 1993, ''Linear Programs and Related Problems'', Academic Press. (elementary)</ref><ref>Robert J. Vanderbei, ''Linear Programming: Foundations and Extensions'', 3rd ed., International Series in Operations Research & Management Science, Vol. 114, Springer Verlag, 2008. <nowiki>ISBN 978-0-387-74387-5</nowiki>.</ref> | |||
== Numerical Example == | |||
Considering the following numerical example to gain better understanding: | |||
<math> \max{4x_1+x_2+4x_3}</math> | |||
with the following constraints: | |||
<math> \begin{align} | |||
2x_1 + x_2 + x_3 &\leq 2 \\ | |||
x_1 + 2x_2 +3x_3 &\leq 4\\ | |||
2x_1 + 2x_2 + x_3 &\leq 8 \\ | |||
x_1,x_2,x_3 &\geq 0 | |||
\end{align}</math> | |||
With adding slack variables to get the following equations: | |||
<math> \begin{align} | |||
z - 4x_1 - x_2 -4x_3 &= 0 \\ | |||
2x_1 + x_2 + x_3 + s_1 &= 2 \\ | |||
x_1 + 2x_2 + 3x_3 + s_2 &= 4\\ | |||
2x_1 + 2x_2 + x_3 + s_3 &= 8 \\ | |||
x_1,x_2,x_3,s_1,s_2,s_3 &\geq 0 \end{align} </math> | |||
The simplex tableau can be derived as following: | |||
<math> | |||
\begin{array}{c c c c c c c | r} | |||
x_1 & x_2 & x_3 & s_1 & s_2 & s_3 & z & b \\ | |||
\hline | |||
2 & 1 & 1 & 1 & 0 & 0 & 0 & 2 \\ | |||
1 & 2 & 3 & 0 & 1 & 0 & 0 & 4 \\ | |||
2 & 2 & 1 & 0 & 0 & 1 & 0 & 8 \\ | |||
\hline | |||
-4 & -1 & -4 & 0 & 0 & 0 & 1 & 0 | |||
\end{array} </math> | |||
In the last row, the column with the smallest value should be selected. Although there are two smallest values, the result will be the same no matter of which one is selected first. For this solution, the first column is selected. After the least coefficient is found, the pivot process will be conducted by searching for the coefficient <math> \frac{b_i}{x_1} </math>. Since the coefficient in the first row is 1 and 4 for the second row, the first row should be pivoted. And following tableau can be created: | |||
<math> | |||
\begin{array}{c c c c c c c | r} | |||
x_1 & x_2 & x_3 & s_1 & s_2 & s_3 & z & b \\ | |||
\hline | |||
1 & 0.5 & 0.5 & 0.5 & 0 & 0 & 0 & 1 \\ | |||
1 & 2 & 3 & 0 & 1 & 0 & 0 & 4 \\ | |||
2 & 2 & 1 & 0 & 0 & 1 & 0 & 8 \\ | |||
\hline | |||
-4 & -1 & -4 & 0 & 0 & 0 & 1 & 0 | |||
\end{array} </math> | |||
By performing the row operation still every other rows (other than first row) in column 1 are zeroes: | |||
<math> | |||
\begin{array}{c c c c c c c | r} | |||
x_1 & x_2 & x_3 & s_1 & s_2 & s_3 & z & b \\ | |||
\hline | |||
1 & 0.5 & 0.5 & 0.5 & 0 & 0 & 0 & 1 \\ | |||
0 & 1.5 & 2.5 & -0.5 & 1 & 0 & 0 & 3 \\ | |||
0 & 1 & 0 & -1 & 0 & 1 & 0 & 6 \\ | |||
\hline | |||
0 & 1 & -2 & 2 & 0 & 0 & 1 & 4 | |||
\end{array} </math> | |||
Because there is one negative value in last row, the same processes should be performed again. The smallest value in the last row is in the third column. And in the third column, the second row has the smallest coefficients of <math> \frac{b_i}{x_3}</math> which is 1.2. Thus, the second row will be selected for pivoting. The simplex tableau is the following: | |||
<math> | |||
\begin{array}{c c c c c c c | r} | |||
x_1 & x_2 & x_3 & s_1 & s_2 & s_3 & z & b \\ | |||
\hline | |||
1 & 0.5 & 0.5 & 0.5 & 0 & 0 & 0 & 1 \\ | |||
0 & 0.6 & 1 & -0.2 & 0.4 & 0 & 0 & 1.2 \\ | |||
0 & 1 & 0 & -1 & 0 & 1 & 0 & 6 \\ | |||
\hline | |||
0 & 1 & -2 & 2 & 0 & 0 & 1 & 4 | |||
\end{array} </math> | |||
By performing the row operation to make other columns 0's, the following could be derived | |||
<math> | |||
\begin{array}{c c c c c c c | r} | |||
x_1 & x_2 & x_3 & s_1 & s_2 & s_3 & z & b \\ | |||
\hline | |||
1 & 0.2 & 0 & 0.6 & -0.2 & 0 & 0 & 0.4 \\ | |||
0 & 0.6 & 1 & -0.2 & 0.4 & 0 & 0 & 1.2 \\ | |||
0 & -0.1 & 0 & 0.2 & 0.6 & -1 & 0 & -4.2 \\ | |||
\hline | |||
0 & 2.2 & 0 & 1.6 & 0.8 & 0 & 1 & 6.4 | |||
\end{array} </math> | |||
There is no need to further conduct calculation since all values in the last row are non-negative. From the tableau above, <math>x_1</math>, <math> x_3</math> and <math>z</math> are basic variables since all rows in their columns are 0's except one row is 1.Therefore, the optimal solution will be <math>x_1 = 0.4</math>, <math>x_2 = 0</math>, <math>x_3 = 1.2</math>, achieving the maximum value: <math>z = 6.4</math> | |||
== Application == | |||
The simplex method can be used in many programming problems since those will be converted to LP (Linear Programming) and solved by the simplex method. Besides the mathematical application, much other industrial planning will use this method to maximize the profits or minimize the resources needed. | |||
=== Mathematical Problem === | |||
The simplex method is commonly used in many programming problems. Due to the heavy load of computation on the non-linear problem, many non-linear programming(NLP) problems cannot be solved effectively. Consequently, many NLP will rely on the LP solver, namely the simplex method, to do some of the work in finding the solution (for instance, the upper or lower bound of the feasible solution), or in many cases, those NLP will be wholly linearized to LP and solved from the simplex method.<ref name=":0" /> Other than solving the problems, simplex method can also be used reliably to support the LP's solution from other theorem, for instance the [[wikipedia:Farkas'_lemma#:~:text=Farkas'%20lemma%20is%20a%20solvability,the%20Hungarian%20mathematician%20Gyula%20Farkas.&text=Farkas'%20lemma%20belongs%20to%20a,two%20systems%20has%20a%20solution.|Farkas' theorem]] in which Simplex method proves the suggested feasible solutions.<sup>[1]</sup> Besides solving the problems, the Simplex method can also enlighten the scholars with the ways of solving other problems, for instance, Quadratic Programming (QP).<ref>Wolfe, P. (1959). The simplex method for quadratic programming. ''Econometrica,'' ''27''(3), 382. doi:10.2307/1909468</ref> For some QP problems, they have linear constraints to the variables which can be solved analogous to the idea of the Simplex method. | |||
=== Industrial Application === | |||
The industries from different fields will use the simplex method to plan under the constraints. With considering that it is usually the case that the constraints or tradeoffs and desired outcomes are linearly related to the controllable variables, many people will develop the models to solve the LP problem via the simplex method, for instance, the agricultural and economic problems | |||
Farmers usually need to rationally allocate the existed resources to obtain the maximum profits. The potential constraints are raised from multiple perspectives including policy restriction, budget concerns as well as farmland area. Farmers may incline to use the simplex-method-based model to have a better plan, as those constraints may be constant in many scenarios and the profits are usually linearly related to the farm production, thereby forming the LP problem. Currently, there is an existing plant-model that can accept inputs such as price, farm production, and return the optimal plan to maximize the profits with given information.<ref>Hua, W. (1998). [https://shareok.org/bitstream/handle/11244/12005/Thesis-1998-H8735a.pdf?sequence=1 Application of the revised simplex method to the farm planning model].</ref> | |||
Besides agricultural purposes, the Simplex method can also be used by enterprises to make profits. The rational sale-strategy will be indispensable to the successful practice of marketing. Since there are so many enterprises international wide, the marketing strategy from enamelware is selected for illustration. After widely collecting the data of the quality of varied products manufactured, cost of each and popularity among the customers, the company may need to determine which kind of products well worth the investment and continue making profits as well as which won't. Considering the cost and profit factors are linearly dependent on the production, economists will suggest an LP model that can be solved via the simplex method.<ref>Nikitenko, A. V. (1996). Economic analysis of the potential use of a simplex method in designing the sales strategy of an enamelware enterprise. ''Glass and Ceramics,'' ''53''(12), 367-369. doi:10.1007/bf01129674.</ref> | |||
The above professional fields are only the tips of the iceberg to the simplex method application. Many other fields will use this method since the LP problem is gaining popularity in recent days and the simplex method plays a crucial role in solving those problems. | |||
< | == Conclusion == | ||
It is indisputable to acknowledge the influence of the Simplex method to programming, as this method won the 'National Medal of Science' to its inventor, George Dantzig.<ref>Cottle, R., Johnson, E. and Wets, R. (2007). George B. Dantzig (1914–2005). ''Notices Amer. Math. Soc.'' 54, 344–362.</ref> Not only for its wide usage in the mathematic models and industrial manufacture, but the Simplex method also provides a new perspective in solving the inequality problems. As its contribution to the programming substantially boosts the advancement of the current technology and economy from making the optimal plan with the constraints. Nowadays, with the development of technology and economics, the Simplex method is substituted with some more advanced solvers which can solve the problems with faster speed and handle a larger amount of constraints and variables, but this innovative method marks the creativity at that age and continuously offer the inspiration to the upcoming challenges. | |||
== References == | |||
<references /> | |||
Latest revision as of 08:26, 5 October 2021
Author: Guoqing Hu (SysEn 6800 Fall 2020)
Introduction
Simplex algorithm (or Simplex method) is a widely-used algorithm to solve the Linear Programming(LP) optimization problems. The simplex algorithm can be thought of as one of the elementary steps for solving the inequality problem, since many of those will be converted to LP and solved via Simplex algorithm.[1] Simplex algorithm has been proposed by George Dantzig, initiated from the idea of step by step downgrade to one of the vertices on the convex polyhedral.[2] "Simplex" could be possibly referred to as the top vertex on the simplicial cone which is the geometric illustration of the constraints within LP problems.[3]
Algorithmic Discussion
There are two theorems in LP:
- The feasible region for an LP problem is a convex set (Every linear equation's second derivative is 0, implying the monotonicity of the trend). Therefore, if an LP has an optimal solution, there must be an extreme point of the feasible region that is optimal
- For an LP optimization problem, there is only one extreme point of the LP's feasible region regarding every basic feasible solution. Plus, there will be a minimum of one basic feasible solution corresponding to every extreme point in the feasible region.[4]
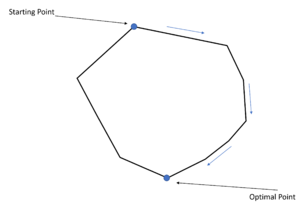
Based on the two theorems above, the geometric illustration of the LP problem could be depicted. Each line of this polyhedral will be the boundary of the LP constraints, in which every vertex will be the extreme points according to the theorem. The simplex method is the way to adjust the nonbasic variables to travel to different vertex till the optimum solution is found.[5]
Consider the following expression as the general linear programming problem standard form:
With the following constraints:
The first step of the simplex method is to add slack variables and symbols which represent the objective functions:
The new introduced slack variables may be confused with the original values. Therefore, it will be convenient to add those slack variables to the end of the list of x-variables with the following expression:
With the progression of simplex method, the starting dictionary (which is the equations above) switches between the dictionaries in seeking for optimal values. Every dictionary will have m basic variables which form the feasible area, as well as n non-basic variables which compose the objective function. Afterward, the dictionary function will be written in the form of:
Where the variables with bar suggest that those corresponding values will change accordingly with the progression of the simplex method. The observation could be made that there will specifically one variable goes from non-basic to basic and another acts oppositely. This kind of variable is referred to as the entering variable. Under the goal of increasing , the entering variables are selected from the set {1,2,...,n}. As long as there are no repetitive entering variables can be selected, the optimal values will be found. The decision of which entering variable should be selected at first place should be made based on the consideration that there usually are multiple constraints (n>1). For the Simplex algorithm, the coefficient with the least value is preferred since the major objective is maximization.
The leaving variables are defined as which go from basic to non-basic. The reason of their existence is to ensure the non-negativity of those basic variables. Once the entering variables are determined, the corresponding leaving variables will change accordingly from the equation below:
Since the non-negativity of entering variables should be ensured, the following inequality can be derived:
Where is immutable. The minimum should be zero to get the minimum value since this cannot be negative. Therefore, the following equation should be derived:
Due to the nonnegativity of all variables, the value of should be raised to the largest of all of those values calculated from above equation. Hence, the following equation can be derived:
Once the leaving-basic and entering-nonbasic variables are chosen, reasonable row operation should be conducted to switch from the current dictionary to the new dictionary, as this step is called pivot.[4]
As in the pivot process, the coefficient for the selected pivot element should be one, meaning the reciprocal of this coefficient should be multiplied to every element within this row. Afterward, multiplying this specific row with corresponding coefficients and adding this to different rows, one should get 0 values for all other entries in this pivot element's column.
If there are any negative variables after the pivot process, one should continue finding the pivot element by repeating the process above. At once there are no more negative values for basic and non-basic variables. The optimal solution is found.[6][7]
Numerical Example
Considering the following numerical example to gain better understanding:
with the following constraints:
With adding slack variables to get the following equations:
The simplex tableau can be derived as following:
In the last row, the column with the smallest value should be selected. Although there are two smallest values, the result will be the same no matter of which one is selected first. For this solution, the first column is selected. After the least coefficient is found, the pivot process will be conducted by searching for the coefficient . Since the coefficient in the first row is 1 and 4 for the second row, the first row should be pivoted. And following tableau can be created:
By performing the row operation still every other rows (other than first row) in column 1 are zeroes:
Because there is one negative value in last row, the same processes should be performed again. The smallest value in the last row is in the third column. And in the third column, the second row has the smallest coefficients of which is 1.2. Thus, the second row will be selected for pivoting. The simplex tableau is the following:
By performing the row operation to make other columns 0's, the following could be derived
There is no need to further conduct calculation since all values in the last row are non-negative. From the tableau above, , and are basic variables since all rows in their columns are 0's except one row is 1.Therefore, the optimal solution will be , , , achieving the maximum value:
Application
The simplex method can be used in many programming problems since those will be converted to LP (Linear Programming) and solved by the simplex method. Besides the mathematical application, much other industrial planning will use this method to maximize the profits or minimize the resources needed.
Mathematical Problem
The simplex method is commonly used in many programming problems. Due to the heavy load of computation on the non-linear problem, many non-linear programming(NLP) problems cannot be solved effectively. Consequently, many NLP will rely on the LP solver, namely the simplex method, to do some of the work in finding the solution (for instance, the upper or lower bound of the feasible solution), or in many cases, those NLP will be wholly linearized to LP and solved from the simplex method.[1] Other than solving the problems, simplex method can also be used reliably to support the LP's solution from other theorem, for instance the Farkas' theorem in which Simplex method proves the suggested feasible solutions.[1] Besides solving the problems, the Simplex method can also enlighten the scholars with the ways of solving other problems, for instance, Quadratic Programming (QP).[8] For some QP problems, they have linear constraints to the variables which can be solved analogous to the idea of the Simplex method.
Industrial Application
The industries from different fields will use the simplex method to plan under the constraints. With considering that it is usually the case that the constraints or tradeoffs and desired outcomes are linearly related to the controllable variables, many people will develop the models to solve the LP problem via the simplex method, for instance, the agricultural and economic problems
Farmers usually need to rationally allocate the existed resources to obtain the maximum profits. The potential constraints are raised from multiple perspectives including policy restriction, budget concerns as well as farmland area. Farmers may incline to use the simplex-method-based model to have a better plan, as those constraints may be constant in many scenarios and the profits are usually linearly related to the farm production, thereby forming the LP problem. Currently, there is an existing plant-model that can accept inputs such as price, farm production, and return the optimal plan to maximize the profits with given information.[9]
Besides agricultural purposes, the Simplex method can also be used by enterprises to make profits. The rational sale-strategy will be indispensable to the successful practice of marketing. Since there are so many enterprises international wide, the marketing strategy from enamelware is selected for illustration. After widely collecting the data of the quality of varied products manufactured, cost of each and popularity among the customers, the company may need to determine which kind of products well worth the investment and continue making profits as well as which won't. Considering the cost and profit factors are linearly dependent on the production, economists will suggest an LP model that can be solved via the simplex method.[10]
The above professional fields are only the tips of the iceberg to the simplex method application. Many other fields will use this method since the LP problem is gaining popularity in recent days and the simplex method plays a crucial role in solving those problems.
Conclusion
It is indisputable to acknowledge the influence of the Simplex method to programming, as this method won the 'National Medal of Science' to its inventor, George Dantzig.[11] Not only for its wide usage in the mathematic models and industrial manufacture, but the Simplex method also provides a new perspective in solving the inequality problems. As its contribution to the programming substantially boosts the advancement of the current technology and economy from making the optimal plan with the constraints. Nowadays, with the development of technology and economics, the Simplex method is substituted with some more advanced solvers which can solve the problems with faster speed and handle a larger amount of constraints and variables, but this innovative method marks the creativity at that age and continuously offer the inspiration to the upcoming challenges.
References
- ↑ 1.0 1.1 Linear complementarity, linear and nonlinear programming Internet Edition.
- ↑ Dantzig, G. B. (1987, May). Origins of the simplex method.
- ↑ Strang, G. (1987). Karmarkar’s algorithm and its place in applied mathematics. The Mathematical Intelligencer, 9(2), 4-10. doi:10.1007/bf03025891.
- ↑ 4.0 4.1 Vanderbei, R. J. (2000). Linear programming: Foundations and extensions. Boston: Kluwer.
- ↑ Sakarovitch M. (1983) Geometric Interpretation of the Simplex Method. In: Thomas J.B. (eds) Linear Programming. Springer Texts in Electrical Engineering. Springer, New York, NY. https://doi.org/10.1007/978-1-4757-4106-3_8
- ↑ Evar D. Nering and Albert W. Tucker, 1993, Linear Programs and Related Problems, Academic Press. (elementary)
- ↑ Robert J. Vanderbei, Linear Programming: Foundations and Extensions, 3rd ed., International Series in Operations Research & Management Science, Vol. 114, Springer Verlag, 2008. ISBN 978-0-387-74387-5.
- ↑ Wolfe, P. (1959). The simplex method for quadratic programming. Econometrica, 27(3), 382. doi:10.2307/1909468
- ↑ Hua, W. (1998). Application of the revised simplex method to the farm planning model.
- ↑ Nikitenko, A. V. (1996). Economic analysis of the potential use of a simplex method in designing the sales strategy of an enamelware enterprise. Glass and Ceramics, 53(12), 367-369. doi:10.1007/bf01129674.
- ↑ Cottle, R., Johnson, E. and Wets, R. (2007). George B. Dantzig (1914–2005). Notices Amer. Math. Soc. 54, 344–362.





























