Simplex algorithm
Author: Guoqing Hu (SysEn 6800 Fall 2020)
Steward: Allen Yang, Fengqi You
Introduction
Simplex algorithm (or Simplex method) is a widely-used algorithm to solve the Linear Programming(LP). Simplex algorithm can be thought as one of the elementary steps for solving the inequality problem, since many of those will be converted to LP and solved via Simplex algorithm[1]. Simplex algorithm has been proposed by George Dantzig, initiated from the idea of step by step downgrade to one of the vortices on the convex polyhedral[2]. "Simplex" could be possibly referred as the top vertex on the simplicial cone which is the geometric illustration of the constraints within Linear Problem[3].
Algorithmic Discussion
There are two theorem in LP:
- The feasible region for any LP problem is a convex set (Every linear equation's second derivative is 0, implying the monotonicity of the trend). Therefore, if an LP has an optimal solution, there must be an extreme point of the feasible region that is optimal
- For any LP, there is only one extreme point of the LP's feasible region regarding to every basic feasible solution. Plus, there will be at minimum of one basic feasible solution corresponding to every extreme point in the feasible region.[4]
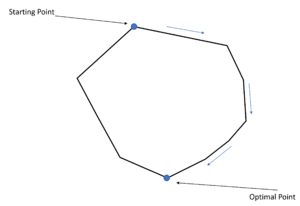
Based on two theorems above, the geometric illustration of the LP problem could be depicted. Each line of this polyhedral will be the boundary of the LP constraints, in which every vertex will be the extreme points according to the theorem. Simplex method is the way to reasonably sort out the shortest path to the optimal solutions.
Consider the following expression as the general linear programming problem standard form:
With the following constraints:
The first step of the simplex method is to add slack variables and symbols which represent the objective functions:
The new introduced slack variables may be confused with the original values. Therefore, it will be convenient to add those slack variables to the end of the list of x-variables with the following expression:
With the progression of simplex method, the starting dictionary (which is the equations above) switches between the dictionaries in seeking for optimal values. Every dictionary will have m basic variables which form the feasible area, as well as n non-basic variables which compose the objective function. Afterward, the dictionary function will be written in the form of:
Where the variables with bar suggest that those corresponding values will change accordingly with the progression of simplex method. The observation could be made that there will specifically one variable goes from non-basic to basic and one acts oppositely. As this kind of variable is referred as entering variable. Under the goal of increasing Φ, the entering variables are selected from the set {1,2,...,n}. As long as there are no repetitive entering variables can be selected, the optimal values will be found. The decision of which entering variable should be selected at first place should be made based on the consideration that there usually are multiple constraints (n>1). For Simplex algorithm, the coefficient with least value is preferred since the major objective is maximization.
The leaving variables are defined as which go from basic to non-basic. The reason of their existence is to ensure the non-negativity of those basic variables. Once the entering variables are determined, the corresponding leaving variables will change accordingly from the equation below:
Since the non-negativity of entering variables should be ensured, the following inequality can be derived:
Where xk is immutable. The minimum xi should be zero to get the minimum value since this cannot be negative. Therefore, the following equation should be derived:
Due the nonnegativity of all variables, the value of xk should be raised to the largest of all of those values calculated from above equation. Hence, the following equation can be derived:
Once the leaving-basic and entering-nonbasic variables are chosen, reasonable row operation should be conducted to switch from current dictionary to the new dictionary, as this step is referred as pivot.[4]
Numerical Example
Considering the following numerical example to gain better understanding:
with the following constraints:
With adding slack variables to get the following equations:
The simplex tableau can be derived as following:
In the last row, the column with the smallest value should be selected. Although there are two smallest values, the result will be the same no matter of which one is selected first. For this solution, the first column is selected. After the least coefficient is found, the pivot process will be conducted by searching for the coefficient . Since the value for the first row is 1 and second row is 4. Thus, the first row should be pivoted. And following tableau can be created:
By performing the row operation still every other rows (other than first row) in column 1 are zeroes:
Because there is one negative value in last row, the same processes should be performed again. The smallest value in the last row is in the third column. And in the third column, the second row has the smallest coefficients of which is 1.2. Thus, the second row will be selected for pivoting. The simplex tableau is the following:
By performing the row operation to make other columns 0's, the following could be derived
From the tableau above, , and are basic variables since the column in those rows are 0's. Thus, the following equations could be concluded from the tableau:
Therefore, the optimal solution will be , , , achieving the maximum value:

























