Trust-region methods: Difference between revisions
No edit summary |
|||
| Line 6: | Line 6: | ||
=Methodology and theory= | =Methodology and theory= | ||
'''Cauchy point calculation''' | '''Cauchy point calculation''' | ||
Similar to line serach method which do not require optimal step lengths to be convergent, trust-region method is suffficient for global convergence purpose to find an approximate solution pk that lies within trust region. | |||
<math>p_{c}^{K}=-\tau _{k}\frac{\Delta k}{\left \| \bigtriangledown f_{k} \right \|}\bigtriangledown f_{k}</math> | <math>p_{c}^{K}=-\tau _{k}\frac{\Delta k}{\left \| \bigtriangledown f_{k} \right \|}\bigtriangledown f_{k}</math> | ||
| Line 15: | Line 17: | ||
'''Improving on the couchy point''' | '''Improving on the couchy point''' | ||
The reason we improving on the couchy point is that we just implementing the steepest decent method with a particular choice of step length by using cauchy point. However, steepest decent performs poorly even if an optimial step length is used at every iteration. | |||
<math>min m(p)=f+g^{T}p+\frac{1}{2}p^{T}B_{p} </math>, <math>p\in R^{n} </math> s.t. <math>\left \| p \right \|\leq \Delta </math> | <math>min m(p)=f+g^{T}p+\frac{1}{2}p^{T}B_{p} </math>, <math>p\in R^{n} </math> s.t. <math>\left \| p \right \|\leq \Delta </math> | ||
| Line 20: | Line 24: | ||
'''Dogleg method''' | '''Dogleg method''' | ||
The dogleg method chooses p to minimize the model m along this path.Furthermore,gogled method is limited to | |||
the trust-region bound. Since the dogleg path interacts the trust region at most one points and intersectin can be computed anlytically, there is no need to conduct a search. | |||
<math>\tilde{p}=\tau p^{U} </math>, when <math>0\leq \tau \leq 1 </math> | <math>\tilde{p}=\tau p^{U} </math>, when <math>0\leq \tau \leq 1 </math> | ||
| Line 25: | Line 34: | ||
<math>\tilde{p}= p^{U}+\left (\tau -1 \right )\left ( p^{B}-p^{U} \right ) </math>, when <math>1\leq \tau \leq 2 </math> | <math>\tilde{p}= p^{U}+\left (\tau -1 \right )\left ( p^{B}-p^{U} \right ) </math>, when <math>1\leq \tau \leq 2 </math> | ||
where <math>p^{U}=-\frac{g^{T}g}{g^{T}Bg}g </math>, <math>p^{B} </math>=opitimal | where <math>p^{U}=-\frac{g^{T}g}{g^{T}Bg}g </math>, <math>p^{B} </math>=opitimal solution of quadratic model | ||
| Line 32: | Line 41: | ||
Given<math>\epsilon > 0 </math> | Given<math>\epsilon > 0 </math> | ||
Set<math>p_{0}=0,r_{0}=g,d_{0}=-r_{0} </math> | Set <math>p_{0}=0,r_{0}=g,d_{0}=-r_{0} </math> | ||
if<math>\left \| r_{0} \right \|< \epsilon </math> | if<math>\left \| r_{0} \right \|< \epsilon </math> | ||
| Line 46: | Line 55: | ||
return p; | return p; | ||
Set | Set <math>\alpha _{j}=r_{j}^{T}r_{j}/d_{j}^{T}Bd_{j}</math> | ||
Set <math> p_{j+1}=p_{j}+\alpha _{j}d_{j}</math> | |||
if <math>\left \| p_{j+1} \right \|\geq \Delta</math> | |||
Find <math>\tau \geq 0</math> such that <math>p=p_{j}+\tau d_{j}</math> satisfies <math>\left \| p \right \|=\Delta </math> | |||
return p; | |||
Set <math>r_{j+1}=r_{j}+\alpha _{j}Bd_{j}</math> | |||
if <math> \left \| r_{j+1} \right \|< \epsilon \left \| r_{0} \right \|</math> | |||
return <math>p=p_{j+1}</math> | |||
Set <math>\beta _{j+1} = r_{j+1}^{T}r_{j+1}/r_{j}^{T}r_{j}</math> | |||
Set <math>d_{j+1}= r_{j+1}+ \beta _{j+1}d_{j}</math> | |||
end(for) | |||
=Numerical example= | =Numerical example= | ||
Revision as of 22:01, 28 November 2021
Autor: Chun-Yu Chou (cc2398), Ting-Guang Yeh (ty262), Yun-Chung Pan (yp392), Chen-Hua Wang (cw893), Fall 2021
Introduction
Problem formulation
Methodology and theory
Cauchy point calculation
Similar to line serach method which do not require optimal step lengths to be convergent, trust-region method is suffficient for global convergence purpose to find an approximate solution pk that lies within trust region.
if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigtriangledown f_{k}^{T}B_{k}\bigtriangledown f_{k}\leq 0} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau _{k}=1}
otherewise, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau _{k}= min\left ( \left \| \bigtriangledown f_{k} \right \|^{3}/\left ( \bigtriangleup _{k}\bigtriangledown f_{k}^{T}B_{k}\bigtriangledown f_{k} \right ),1 \right ) }
Improving on the couchy point
The reason we improving on the couchy point is that we just implementing the steepest decent method with a particular choice of step length by using cauchy point. However, steepest decent performs poorly even if an optimial step length is used at every iteration.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle min m(p)=f+g^{T}p+\frac{1}{2}p^{T}B_{p} } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p\in R^{n} } s.t. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \| p \right \|\leq \Delta }
Dogleg method
The dogleg method chooses p to minimize the model m along this path.Furthermore,gogled method is limited to
the trust-region bound. Since the dogleg path interacts the trust region at most one points and intersectin can be computed anlytically, there is no need to conduct a search.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{p}=\tau p^{U} }
, when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0\leq \tau \leq 1 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{p}= p^{U}+\left (\tau -1 \right )\left ( p^{B}-p^{U} \right ) } , when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1\leq \tau \leq 2 }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p^{U}=-\frac{g^{T}g}{g^{T}Bg}g } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p^{B} } =opitimal solution of quadratic model
Steihau's approach
GivenFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon > 0 }
Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{0}=0,r_{0}=g,d_{0}=-r_{0} }
ifFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \| r_{0} \right \|< \epsilon }
return p=p0
for j=0,1,2,.....
if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{j}^{T}Bd_{j}\leq 0 }
Find Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau } such that minimizes m(p) and satisfiesFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \| p \right \|=\Delta }
return p;
Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha _{j}=r_{j}^{T}r_{j}/d_{j}^{T}Bd_{j}}
Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{j+1}=p_{j}+\alpha _{j}d_{j}}
if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \| p_{j+1} \right \|\geq \Delta}
Find Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau \geq 0} such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p=p_{j}+\tau d_{j}} satisfies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \| p \right \|=\Delta }
return p;
Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{j+1}=r_{j}+\alpha _{j}Bd_{j}}
if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \| r_{j+1} \right \|< \epsilon \left \| r_{0} \right \|}
return Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p=p_{j+1}}
Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta _{j+1} = r_{j+1}^{T}r_{j+1}/r_{j}^{T}r_{j}}
Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{j+1}= r_{j+1}+ \beta _{j+1}d_{j}}
end(for)
Numerical example
Here we will use the trust-region method to solve a classic optimization problem, the Rosenbrock function. The Rosenbrock function is a non-convex function, introduced by Howard H. Rosenbrock in 1960, which is often used as a performance test problem for optimization algorithms. This problem is solved using MATLAB's fminunc as the solver, with 'trust-region' as the solving algorithm which uses the preconditioned conjugate method.
The function is defined by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \min f(x,y)=100(y-x^2)^2+(1-x)^2}
The starting point chosen is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0 } .
Iteration Process
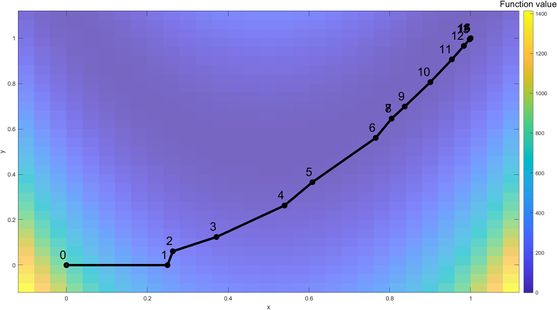
Iteration 1: The algorithm starts from the initial point of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0 } . The Rosenbrock function is visualized with a color coded map. For the first iteration, a full step was taken and the optimal solution (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0.25} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0 } ) within the trust-region is denoted as a red dot.
Iteration 2: Start with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0.25 } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0 } . The new iteration gives a good prediction, which increases the trust-region's size. The new optimal solution within the trust-region is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0.263177536 } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0.061095029 } .
Iteration 3: Start with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0.263177536 }
, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0.061095029 }
. The new iteration gives a poor prediction, which decreases the trust-region's size to improve the model's validity. The new optimal solution within the trust-region is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0.371151679 }
, .
...
Iteration 7: Start with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0.765122406 } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0.560476539 } . The new iteration gives a poor prediction, which decreases the trust-region's size to improve the model's validity. The new optimal solution within the trust-region is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0.804352654 } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0.645444179 } .
Iteration 8: Start with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0.804352654 }
, .The new iteration gives a poor prediction, therefore current best solution is unchanged and the radius for the trust-region is decreased.
...
At the 16th iteration, the global optimal solution is found, , .
| Iterations | f(x) | x | y | Norm of step | First-order optimality |
|---|---|---|---|---|---|
| 1 | 1 | 0.25 | 0 | 1 | 2 |
| 2 | 0.953125 | 0.263178 | 0.061095 | 0.25 | 12.5 |
| 3 | 0.549578 | 0.371152 | 0.124076 | 0.0625 | 1.63 |
| 4 | 0.414158 | 0.539493 | 0.262714 | 0.125 | 2.74 |
| 5 | 0.292376 | 0.608558 | 0.365573 | 0.218082 | 5.67 |
| 6 | 0.155502 | 0.765122 | 0.560477 | 0.123894 | 0.954 |
| 7 | 0.117347 | 0.804353 | 0.645444 | 0.25 | 7.16 |
| 8 | 0.0385147 | 0.804353 | 0.645444 | 0.093587 | 0.308 |
| 9 | 0.0385147 | 0.836966 | 0.69876 | 0.284677 | 0.308 |
| 10 | 0.0268871 | 0.90045 | 0.806439 | 0.0625 | 0.351 |
| 11 | 0.0118213 | 0.953562 | 0.90646 | 0.125 | 1.38 |
| 12 | 0.0029522 | 0.983251 | 0.9659 | 0.113247 | 0.983 |
| 13 | 0.000358233 | 0.99749 | 0.994783 | 0.066442 | 0.313 |
| 14 | 1.04121e-05 | 0.999902 | 0.999799 | 0.032202 | 0.0759 |
| 15 | 1.2959e-08 | 1 | 1 | 0.005565 | 0.00213 |
| 16 | 2.21873e-14 | 1 | 1 | 0.000224 | 3.59E-06 |
Applications
Approaches for a convex model problem
- Levenberg–Marquardt Steps
The objective function is iteratively approximated by a quadratic surface, and the estimate is updated. However, this method may fail to converge if the initial guess is too large or
too small. The trust region methods help to control the trust region size, preventing each step from being too far from the optimum.
- Powell Dogleg Steps
Compared to Levenberg–Marquardt steps, the objective function is iteratively approximated by a linear surface, and the estimate is updated as well. Besides, the Levenberg–
Marquardt steps provide an exact solution to the model problem, while the dogleg method provides only an approximate solution.
Approaches for a nonconvex model problem
If the exact Hessian is not positive definite, then a dogleg method that relies on Newton steps may be ascent steps or unbounded steps. Furthermore, the Levenberg–Marquardt method may not be flexible to exploit the size of the trust region. However, the trust region method can used to iteratively minimize a quadratic model of the Lagrangian subject to a possibly relaxed linearization of the problem constraints and a trust region constraint.





