Trust-region methods

Autor: Chun-Yu Chou, Ting-Guang Yeh, Yun-Chung Pan, Chen-Hua Wang (CHEME 6800, Fall 2021)

Introduction

Trust region method is a numerical optimization method that is employed to solve non-linear programming (NLP) problem. Instead of finding objective solution of the original function f, in each step the method defines a neighborhood around current best solution xk as a trust region f’ (typically by using quadratic model), which is capable of representing the f function appropriately, in order to derive the next point xk+1. Different from line search, the model selects the direction and step size simultaneously. For example, in a minimization problem, if the decrease in the value of optimal solution is not sufficient, we can conclude that the region is too large to get close to the minimizer of the objective function, so we will shrink the f’ to find the solution again. On the other hand, if such decrease is significant, it is believed that the model has adequate representation to the problem. Generally, the step direction depends on extent that the region is altered in the previous iteration.

Methodology and theory

Cauchy point calculation

Similar to line serach method which do not require optimal step lengths to be convergent, trust-region method is suffficient for global convergence purpose to find an approximate solution pk that lies within trust region. Cauchy step $P_{K}^{C}$ is an unexpensive method( no matrix factorization) to solve trust-region subproblem. Furthermore, Cauchy point has been valued due to the fact that it can globally convergent. Following is a closed-form equations of the Cauchy point.

$p_{k}^{c}=-\tau _{k}{\frac {\Delta k}{\left\|\ g_{k}\right\|}}\ g_{k}$

if $g_{k}^{T}B_{k}g_{k}\leq 0$, $\tau _{k}=1$

otherewise, $\tau _{k}=min\left(\left\|\bigtriangledown g_{k}\right\|^{3}/\left(\bigtriangleup _{k}\bigtriangledown g_{k}^{T}B_{k}g_{k}\right),1\right)$

Although it is unexpensive to apply Cauchy point, steepest descent methods sometimes performs poorly. Thus, we introduce some improving strategy. The improvement strategies is based on $B_{k}$ where it contains valid curvature information about the function.

Dogleg method

This method can be used if $B_{k}$ is a positive definite. The dogleg method finds an approximate solution by replacing the curved trajectory

for $p^{*}\left(\bigtriangleup \right)$ with a path consisting of two line segments. It chooses p to minimize the model m along this path, subject to the trust-region bound.

First line segments $p^{U}=-{\frac {g^{T}g}{g^{T}Bg}}g$, where $p^{U}$runs from the origin to the minimizer of m along the steepest descent direction.

While the second line segment run from $p^{U}$to $p^{B}$, we donate this trajectory by ${\tilde {p}}\left(\tau \right)$ for $\tau \in \left[0,2\right]$

Then a V-shaped trajectory can be determined by

${\tilde {p}}=\tau p^{U}$, when $0\leq \tau \leq 1$

${\tilde {p}}=p^{U}+\left(\tau -1\right)\left(p^{B}-p^{U}\right)$, when $1\leq \tau \leq 2$

where $p^{B}$=opitimal solution of quadratic model

Although the dogleg strategy can be adapted to handle indefinite B, there is not much point in doing so because the full step $p^{B}$ is not the unconstrained minimizer of m in this case. Instead, we now describe another strategy, which aims to include directions of negative

curvature in the space of trust-region steps.

Conjugated Gradient Steihaug’s Method ( CG-Steihaug)

This is the most widely used method for the approximate solution of the trust-region problem. The method works for quadratic models $m_{k}$ defined by an arbitrary symmetric $B_{k}$ . Thus, it is not necessary for $B_{k}$ to be positive. CG-Steihaug has the advantage of Cauchy point calculation and Dogleg method which is super-linear convergence rate and unexpensive costs .

Given$\epsilon >0$

Set $p_{0}=0,r_{0}=g,d_{0}=-r_{0}$

if$\left\|r_{0}\right\|<\epsilon$

return $p=p0$

for $j=0,1,2,...$

if $d_{j}^{T}Bd_{j}\leq 0$

Find $\tau$ such that minimizes $m\left(p\right)$ and satisfies$\left\|p\right\|=\Delta$

return p;

Set $\alpha _{j}=r_{j}^{T}r_{j}/d_{j}^{T}Bd_{j}$

Set $p_{j+1}=p_{j}+\alpha _{j}d_{j}$

if $\left\|p_{j+1}\right\|\geq \Delta$

Find $\tau \geq 0$ such that $p=p_{j}+\tau d_{j}$ satisfies $\left\|p\right\|=\Delta$

return p;

Set $r_{j+1}=r_{j}+\alpha _{j}Bd_{j}$

if $\left\|r_{j+1}\right\|<\epsilon \left\|r_{0}\right\|$

return $p=p_{j+1}$

Set $\beta _{j+1}=r_{j+1}^{T}r_{j+1}/r_{j}^{T}r_{j}$

Set $d_{j+1}=r_{j+1}+\beta _{j+1}d_{j}$

end(for)

Global Convergence

$m_{k}\left(0\right)-m_{k}\left(p_{k}\right)\geq c_{1}\left\|\bigtriangledown f_{k}\right\|min\left(\bigtriangleup k,{\frac {\left\|\bigtriangledown f_{k}\right\|}{\left\|B_{k}\right\|}}\right)$

Numerical example

Here we will use the trust-region method to solve a classic optimization problem, the Rosenbrock function. The Rosenbrock function is a non-convex function, introduced by Howard H. Rosenbrock in 1960, which is often used as a performance test problem for optimization algorithms. This problem is solved using MATLAB's fminunc as the solver, with 'trust-region' as the solving algorithm which uses the preconditioned conjugate method.

The function is defined by

$\min f(x,y)=100(y-x^{2})^{2}+(1-x)^{2}$

The starting point chosen is $x=0$ $y=0$.

Trust-region method trajectory of Rosenbrock function starting from (0,0). The data points represent the optimal solutions after each iteration, ending at iteration number 16 (1,1).

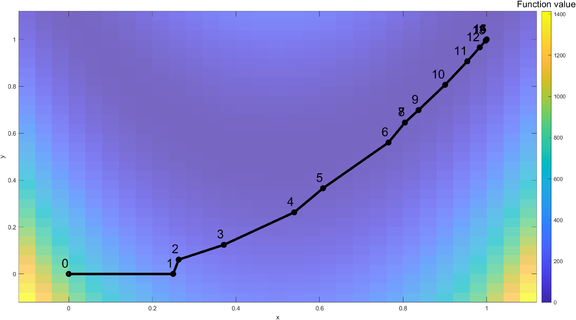
Iteration Process

Iteration 1: The algorithm starts from the initial point of $x=0$, $y=0$. The Rosenbrock function is visualized with a color coded map. For the first iteration, a full step was taken and the optimal solution ($x=0.25$, $y=0$) within the trust-region is denoted as a red dot.

Iteration 2: Start with $x=0.25$, $y=0$. The new iteration gives a good prediction, which increases the trust-region's size. The new optimal solution within the trust-region is $x=0.263177536$, $y=0.061095029$.

Iteration 3: Start with $x=0.263177536$, $y=0.061095029$. The new iteration gives a poor prediction, which decreases the trust-region's size to improve the model's validity. The new optimal solution within the trust-region is $x=0.371151679$, $y=0.124075855$.

...

Iteration 7: Start with $x=0.765122406$, $y=0.560476539$. The new iteration gives a poor prediction, which decreases the trust-region's size to improve the model's validity. The new optimal solution within the trust-region is $x=0.804352654$, $y=0.645444179$.

Iteration 8: Start with $x=0.804352654$, $y=0.645444179$.The new iteration gives a poor prediction, therefore current best solution is unchanged and the radius for the trust-region is decreased.

...

At the 16th iteration, the global optimal solution is found, $x=1$, $y=1$.

Summary of all iterations

Iterations	f(x)	x	y	Norm of step	First-order optimality
1	1	0.25	0	1	2
2	0.953125	0.263178	0.061095	0.25	12.5
3	0.549578	0.371152	0.124076	0.0625	1.63
4	0.414158	0.539493	0.262714	0.125	2.74
5	0.292376	0.608558	0.365573	0.218082	5.67
6	0.155502	0.765122	0.560477	0.123894	0.954
7	0.117347	0.804353	0.645444	0.25	7.16
8	0.0385147	0.804353	0.645444	0.093587	0.308
9	0.0385147	0.836966	0.69876	0.284677	0.308
10	0.0268871	0.90045	0.806439	0.0625	0.351
11	0.0118213	0.953562	0.90646	0.125	1.38
12	0.0029522	0.983251	0.9659	0.113247	0.983
13	0.000358233	0.99749	0.994783	0.066442	0.313
14	1.04121e-05	0.999902	0.999799	0.032202	0.0759
15	1.2959e-08	1	1	0.005565	0.00213
16	2.21873e-14	1	1	0.000224	3.59E-06

Applications

Approaches for a convex model problem

• Levenberg–Marquardt Steps

The objective function is iteratively approximated by a quadratic surface, and the estimate is updated. However, this method may fail to converge if the initial guess is too large or

too small. The trust region methods help to control the trust region size, preventing each step from being too far from the optimum.

• Powell Dogleg Steps

Compared to Levenberg–Marquardt steps, the objective function is iteratively approximated by a linear surface, and the estimate is updated as well. Besides, the Levenberg–

Marquardt steps provide an exact solution to the model problem, while the dogleg method provides only an approximate solution.

Approaches for a nonconvex model problem

If the exact Hessian is not positive definite, then a dogleg method that relies on Newton steps may be ascent steps or unbounded steps. Furthermore, the Levenberg–Marquardt method may not be flexible to exploit the size of the trust region. However, the trust region method can used to iteratively minimize a quadratic model of the Lagrangian subject to a possibly relaxed linearization of the problem constraints and a trust region constraint.

Conclusion

Trusted region is a powerful method that can update the objective function in each step to ensure the model is always getting improved while keeping the previously learnt knowledge as the baseline. Nowadays, trust region algorithms are widely used in machine learning, applied mathematics, physics, chemistry, biology, etc. It is believed that the trust region method will have more far-reaching development in a wider range of fields in the near future.

References

[1] J. Nocedal, S. J. Wright, Numerical Optimization. Springer, 1999.

[2] W. Sun and Y.-x. Yuan, Optimization theory and methods : nonlinear programming. New York: Springer, 2006.

[3] S. Boyd, L. Vandenberghe, Convex Optimization. Cambridge University Press, 2009

[4] Trust region. (2020). Retrieved November 10, 2021, from https://en.wikipedia.org/wiki/Trust_region.