Frank-Wolfe: Difference between revisions
| (81 intermediate revisions by 3 users not shown) | |||
| Line 2: | Line 2: | ||
== Introduction == | == Introduction == | ||
The Frank-Wolfe algorithm is an iterative first-order optimization algorithm for constrained convex optimization, first proposed by Marguerite Frank and Philip Wolfe from Princeton University in 1956.<ref name="Frank">Frank, M. and Wolfe, P. (1956). An algorithm for quadratic programming. ''Naval Research Logistics Quarterly'', 3(1-2):95–110.</ref> It is also known as the “gradient and interpolation” algorithm or sometimes the “conditional gradient method” as it utilizes a simplex method of comparing an initial feasible point with a secondary basic feasible point to maximize the linear constraints in each iteration to find or approximate the optimal solution. | The Frank-Wolfe algorithm is an iterative first-order optimization algorithm for constrained convex optimization, first proposed by Marguerite Frank and Philip Wolfe from Princeton University in 1956.<ref name="Frank">Frank, M. and Wolfe, P. (1956). [https://onlinelibrary.wiley.com/doi/abs/10.1002/nav.3800030109 An algorithm for quadratic programming.] ''Naval Research Logistics Quarterly'', 3(1-2):95–110.</ref> It is also known as the “gradient and interpolation” algorithm or sometimes the “conditional gradient method” as it utilizes a simplex method of comparing an initial feasible point with a secondary basic feasible point to maximize the linear constraints in each iteration, to find or approximate the optimal solution. | ||
Advantages of the Frank-Wolfe algorithm include that it is simple to implement; it results in a projection-free computation (that is, it does not require projections back to the constraint set to ensure feasibility); and it generates solution iterations that are sparse with respect to the constraint set. However, one of the major drawbacks of Frank-Wolfe algorithm is its convergence in practical applications, which can potentially be a computationally intensive process. This has enabled research into new revisions and heuristics to accelerate the algorithm by better aligning the descent direction while still preserving the projection-free property. <ref name="Combettes">Combettes, C.W.. and Pokutta, S. (2020). [https://arxiv.org/abs/2003.06369 Boosting Frank-Wolfe by chasing gradients.] ''International Conference on Machine Learning'' (pp. 2111-2121). PMLR. </ref> Therefore, despite the downside of Frank-Wolfe algorithm, the numerous benefits of this algorithm allow it to be utilized in artificial intelligence, machine learning, traffic assignment, signal processing, and many more applications. | |||
== Theory & Methodology == | == Theory & Methodology == | ||
[[File:Frank-Wolfe algorithm step size.png|thumb|199x199px|The Frank-Wolfe method optimizes by considering the linearization of the objective function '''''f''''' and moving the initial position '''''x''''' towards the minimizer of the linear function.<ref name="Jaggi">Jaggi, M. (2013). Revisiting Frank-Wolfe: Projection-free sparse convex optimization. ''Inerational Conference on Machine Learning'' (pp.427-435). PMLR.</ref>|alt=]] | [[File:Frank-Wolfe algorithm step size.png|thumb|199x199px|'''Figure 1.''' The Frank-Wolfe method optimizes by considering the linearization of the objective function '''''f''''' and moving the initial position '''''x''''' towards the minimizer of the linear function.<ref name="Jaggi">Jaggi, M. (2013). [http://proceedings.mlr.press/v28/jaggi13.html Revisiting Frank-Wolfe: Projection-free sparse convex optimization.] ''Inerational Conference on Machine Learning'' (pp.427-435). PMLR.</ref>|alt=]] | ||
The Frank-Wolfe algorithm uses step size and postulated convexity, which formulates a matrix of positive semidefinite quadratic form. Just like a convex function yields a global minimum at any local minimum on a convex set, by the definition of nonlinear programming, the concave quadratic function would yield a global maximum point at any local maximum on a convex constraint set. | The Frank-Wolfe algorithm uses step size and postulated convexity, which formulates a matrix of positive semidefinite quadratic form. Just like a convex function yields a global minimum at any local minimum on a convex set, by the definition of nonlinear programming, the concave quadratic function would yield a global maximum point at any local maximum on a convex constraint set. | ||
The methodology of the Frank-Wolfe algorithm starts with obtaining the generalized Lagrange multipliers for a quadratic problem, '''PI'''. The found multipliers are considered solutions to a new quadratic problem, '''PII'''. The simplex method is then applied to the new problem, '''PII''', and the gradient and interpolation method is utilized to make incremental steps towards the solution of the original quadratic problem, '''PI'''. This is performed by taking an initial feasible point, obtaining a second basic feasible point along the gradient of the objective function at the initial point, and maximizing the objective function along the segment that joins these two points. The found maximum along the segment is utilized as the starting point for the next iteration.<ref name="Frank" /> Using this method, the values of the objective function converge to zero and in one of the iterations a secondary point will yield a solution. | The methodology of the Frank-Wolfe algorithm starts with obtaining the generalized Lagrange multipliers for a quadratic problem, '''PI'''. The found multipliers are considered solutions to a new quadratic problem, '''PII'''. The simplex method is then applied to the new problem, '''PII''', and the gradient and interpolation method is utilized to make incremental steps towards the solution of the original quadratic problem, '''PI'''. This is performed by taking an initial feasible point, obtaining a second basic feasible point along the gradient of the objective function at the initial point, and maximizing the objective function along the segment that joins these two points. The found maximum along the segment is utilized as the starting point for the next iteration.<ref name="Frank" /> Using this method, the values of the objective function converge to zero and in one of the iterations, a secondary point will yield a solution. | ||
=== Proof === | |||
* <math>X</math> is a <math>[n \times 1]</math> matrix | |||
* <math>A</math> is a <math>[m \times n]</math> matrix | |||
* <math>C</math> is a <math>[n \times n]</math> matrix | |||
* <math>p</math> and <math>b</math> are <math>[1 \times n]</math> and <math>[1 \times m]</math> matrices respectively | |||
* <math>\nabla f(x)</math> is the gradient | |||
== | <math display="block">f(x) = \sum_{j=1}^n p_jx_j - \sum_{j,k=1}^{n,n} X_jC_{jk}X_k</math> | ||
<math display="block">where \; | |||
\sum_{j=1}^n A_{ij}X_j \le b_i \quad (i=1, ..., m) \; and \; X_j \ge 0 \quad (j = 1, ..., n)</math> | |||
===Step 1. Define initial solution=== | <math display="block">\nabla f(x) = \frac{df(x)}{dx}</math> | ||
'''PI''' is represented by the following equations using matrix notation: | |||
<math display="block">\text{Maximize} \qquad f(x) = px' - x'Cx \quad \text{subject to}</math> | |||
<math display="block">(I) = | |||
\begin{cases} | |||
x \ge 0 \\ | |||
Ax \le b | |||
\end{cases}</math> | |||
Since '''PI''' is feasible, any local maximum found that is contained within the convex constraint set is a global maximum. Then by utilizing Kuhn and Tucker's generalizations of the Lagrange Multipliers of the maximization of the objective function <math>f(x)</math>, <math>x_0</math> is considered the solution of '''PI'''. | |||
<math display='block'>\delta f(x_0)x_0 = Max \, [ \, \delta f(x_0)w \, | \, w \ge 0, Aw \le b], \quad where \; w \; \text{is an} \; [n \times 1] \; \text{matrix}</math> | |||
By the Duality Theorem, | |||
<math display='block'>Min \, [ \, ub \, | \, u \ge 0, \, uA \ge \delta f(x_o)], \quad where \; u \; \text{is a} \; [1 \times m] \; \text{matrix}</math> | |||
Therefore, the solution <math>x_0</math> for '''PI''' is only valid if: | |||
<math display='block'>Max \, [ \, \delta f(x_0)x_0 - ub \, | \, u \ge 0, uA \ge \delta f(x_0)] = 0</math> | |||
Since | |||
<math display='block'>\delta f(x) = p - 2x'Cx</math> | |||
Therefore, by the generalization of Lagrangian, <math>g(x,u)</math> is extracted with linear constraints: | |||
<math display='block'>g(x,u) = \delta f(x)x - ub = px - ub - 2x'Cx</math> | |||
<math display='block'>\begin{cases} | |||
x \ge 0, \quad u \ge 0,\\ | |||
Ax \le b, \quad \delta f(x) \le uA | |||
\end{cases}</math> | |||
The completion of the generalized Lagrangian shows that <math>m + n</math> positive variables exist for '''PI''', thus a feasible solution exists. | |||
Based on the concavity of <math>f</math>, | |||
<math display='block'>f(y) - f(x) \le \delta f(x)(y-x)</math> | |||
If <math>(x,u)</math> satisfies <math>g(x,u) \le 0</math> (where ''x'' is a solution if for some <math>u, \; g(x,u)=0</math>), then | |||
<math display='block'>f(y) - f(x) \le \delta f(x)x \le uAy - \delta f(x)x \le ub - \delta f(x)x = -g(x,u)</math> | |||
By the Boundedness Criterion and the Approximation Criterion, | |||
<math display='block'>f(y) - f(x) \le -g(x,u)</math> | |||
The Frank-Wolfe algorithm then adds a non-negative variable to each of the inequalities to obtain the following: | |||
* <math>y</math> and <math>\nu</math> are <math>[m \times 1]</math> and <math>[n \times 1]</math> matrices respectively | |||
<math display='block'>x, \, u, \, y, \, \nu \ge 0</math> | |||
<math display='block'>Ax+y=b</math> | |||
<math display='block'>2Cx+A'u'-\nu '=p'</math> | |||
<math display='block'>g(x,u) = \delta f(x)x-ub = (uA-\nu )x-u(Ax+y) = - \nu x + uy</math> | |||
Thus, the '''PII''' problem is to obtain search vectors to satisfy <math>\nu x+uy=0</math>, and <math>x</math> is considered a solution of '''PI''' if <math>\delta f(x)</math> belongs to the convex cone spanned by the outward normals to the bounding hyperplanes on which <math>x</math> lines as shown in Figure 1. | |||
=== Algorithm === | |||
The Frank-Wolfe algorithm can generally be broken down into five steps as described below. Then the loop of iterations continues throughout ''Step 2'' to ''Step 5'' until the minimum extreme point is identified. | |||
====Step 1. Define initial solution==== | |||
If <math>x</math> is the extreme point, the initial arbitrary basic feasible solution can be considered as: | If <math>x</math> is the extreme point, the initial arbitrary basic feasible solution can be considered as: | ||
<math display=block>x_k \in S \ | <math display="block">x_k \in S \quad where \; k = 0</math> | ||
The letter <math>k</math> denotes the number of iterations. | The letter <math>k</math> denotes the number of iterations. | ||
===Step 2. Determine search direction=== | ====Step 2. Determine search direction==== | ||
Search direction, that is the '''''direction vector''''' is: | Search direction, that is the '''''direction vector''''' is: | ||
| Line 31: | Line 90: | ||
First-order Taylor expansion around <math>x_k</math> and problem is now reformulated to LP: | First-order Taylor expansion around <math>x_k</math> and problem is now reformulated to LP: | ||
<math display=block> | <math display="block">\begin{align}min \quad & z_k(y) = f(x_k) + \nabla f(x_k)^T (y-x_k) \\ | ||
<math display=block> | s.t. \quad & y \in S \\ | ||
\end{align}</math> | |||
====Step 3. Determine step length==== | |||
Step size <math>\alpha_k</math> is defined by the following formula where <math>\alpha_k</math> must be less than 1 to be feasible: | |||
<math display="block">f(x_k + \alpha_k p_k) < f(x_k)</math> | |||
<math display="block">min_{\alpha \in [0,1]} \, f(x_k + \alpha_k p_k)</math> | |||
====Step 4. Set new iteration point==== | |||
<math display="block">x_{k+1} = x_k + \alpha_k p_k</math> | |||
====Step 5. Stopping criterion==== | |||
Check if <math>x_{k+1}</math> is an approximation of <math>x</math>, the extreme point. Otherwise, set <math>k = k + 1</math> and return to ''Step 2'' for the next iteration. | |||
In the Frank-Wolfe algorithm, the value of <math>f</math> descends after each iteration and eventually decreases towards <math>f(x)</math>, the global minimum. | |||
== Numerical Example == | == Numerical Example == | ||
Consider the non-linear problem below: | |||
<math display="block">\begin{align} min \quad &(x-1)^2 + (y-1)^2 \\ | |||
s.t. \quad & 2x+y \leq 6 \\ | |||
& x+2y \leq 6 \\ | |||
& x \geq 0 \\ | |||
& y \geq 0 | |||
\end{align}</math> | |||
'''''ITERATION 1''''' | |||
'''Step 1. Choose a starting point''' | |||
Begin by choosing the feasible point <math>(0,0)</math> and take the partial derivatives of the objective function <math>f</math>. | |||
<math display="block">\delta f_x(x,y) = 2(x-1)=2x-2 | |||
</math> | |||
<math display="block">\delta f_y(x,y) = 2(y-1)=2y-2 | |||
</math> | |||
<math display="block">\therefore \; \nabla f(0,0) = z_0 = [-2, -2] | |||
</math> | |||
'''Step 2. Determine a search direction''' | |||
Obtain the search direction by solving the linear problem that is subject to the constraints defined. | |||
<math display="block"> \nabla f(0,0) \cdot (x,y)^T </math> | |||
The solution of this linear problem is obtained via linear programming algorithm, which is the enumeration with the extreme points in the feasible region. Using the simplex method or an algebraic solver, the solution to linear problem is: | |||
<math display="block"> \nabla f(0,0) \cdot (x,y)^T = (2,2)</math> | |||
Thus, the direction vector <math>p_0</math>for this iteration <math>z_0 </math> is: | |||
<math display="block">\begin{align} p_0 &= (x,y)^T - z_0 \\ | |||
&= [2,2] - [-2,-2] = [4, 4] | |||
\end{align}</math> | |||
'''Step 3. Determine step length''' | |||
Evaluate <math>z_{\alpha_0} = f(4\alpha_0, 4\alpha_0)</math> to obtain step length <math>\alpha_0</math>. | |||
<math display="block">\begin{align} \because \;\; \qquad f &=(4\alpha_0-1)^2 + (4\alpha_0-1)^2 \\ | |||
&= 32\alpha_0^2 -16\alpha_0 +2 \\ | |||
\nabla f(\alpha_0) &= 64\alpha_0 - 16 = 0 \\ | |||
\therefore \qquad \alpha_0 &= 16/64 = 1/4 | |||
\end{align}</math> | |||
'''Step 4. Set new iteration point''' | |||
The next point is determined by the following formula: | |||
<math display="block">\begin{align} x_1 &= x_0 + \alpha_0p_0 \\ | |||
&= [0,0] + 1/4 \cdot [4,4] \\ | |||
\therefore \; x_1 &= [1,1] | |||
\end{align} </math> | |||
'''Step 5. Perform optimality test''' | |||
If the following equation yields a zero, the optimal solution has been found for the problem. | |||
<math display="block">\begin{align} f_1 & = \nabla f(x_0) \cdot p_0 =\nabla f(0,0) \cdot p_0 \\ | |||
& = -2 \cdot 4 + -2 \cdot 4 = -16 | |||
\end{align}</math> | |||
Since the solution is not zero, the extreme point <math>x_0</math> is not optimal and another iteration is required. | |||
'''''ITERATION 2''''' | |||
'''Step 1. Utilize new iteration point as the starting point ''' | |||
From ''Step 4'' in ''Iteration 1'', <math> x_1 = [1,1]</math>. | |||
Therefore, substituting new iteration point <math>x_1</math> into <math>\delta f_x(x,y)</math> and <math>\delta f_y(x,y)</math> from ''Step 1'', | |||
<math display="block">\nabla f(1,1) = z_1 = [0, 0] </math> | |||
Since the gradient of the new starting point is <math>(0,0)</math>, the optimality test for the value of <math>f</math> will always yield <math>0</math>: | |||
<math display="block">f_2 = \nabla f(1,1) \cdot p_1 = [0, 0] \cdot p_1</math> | |||
Thus, the extreme point <math>(1,1)</math> is the optimum solution for this non-linear problem. | |||
== Applications == | == Applications == | ||
=== Image and Video Co-localization === | === Image and Video Co-localization === | ||
[[File:Co-localization with Frank-Wolfe Algorithm.png|thumb|586x586px|The process of co-localization that captures common objects by using bounding boxes.<ref name="Joulin">Joulin, A., Tang, K., & Li, F.F. (2014). Efficient image and video co-localization with frank-wolfe algorithm. ''European Conference on Computer Vision'' (pp. 253-268). Springer, Cham.</ref>|alt=]] | [[File:Co-localization with Frank-Wolfe Algorithm.png|thumb|586x586px|'''Figure 2.''' The process of co-localization that captures common objects by using bounding boxes.<ref name="Joulin">Joulin, A., Tang, K., & Li, F.F. (2014). [https://link.springer.com/chapter/10.1007/978-3-319-10599-4_17 Efficient image and video co-localization with frank-wolfe algorithm.] ''European Conference on Computer Vision'' (pp. 253-268). Springer, Cham.</ref>|alt=]] | ||
The formulation of co-localization using the Frank-Wolfe algorithm involves minimizing a standard quadratic programming problem and reducing it to a succession of simple linear integer problems. The benefit of the algorithm is that it allows many more images to be analyzed simultaneously and more bounding boxes are generated in each image/ video frame for higher accuracy. By relaxing the discrete non-convex set to its convex hull, the constraints that define the original set can now be separated from one image/ video to another. In the case of co-localizing videos, the constraints use the shortest-path algorithm to reach optimization.<ref name="Joulin" /> | Co-localization is one of the programming methods in the machine learning field used to find a common object within a set of images or video frames. The process of co-localization involves first generating multiple candidate bounding boxes for each image/ video frame, then identifying the specific box in each image/ video frame that jointly contains the common object.<ref name="Harzallah">Harzallah, H., Jurie, F., & Schmid, C. (2009). [https://ieeexplore.ieee.org/document/5459257 Combining efficient object localization and image classification.] ''2009 IEEE 12th international conference on computer vision'' (pp. 237-244). IEEE.</ref> This technique is extremely important for analyzing online data. By being able to recognize the common objects, visual concepts can be tagged into specific labels, thus leveraging useful data for other marketing and product design purposes. Such development is especially useful for image and video hosting services such as Flickr and YouTube. | ||
The formulation of co-localization using the Frank-Wolfe algorithm involves minimizing a standard quadratic programming problem and reducing it to a succession of simple linear integer problems. The benefit of the algorithm is that it allows many more images to be analyzed simultaneously and more bounding boxes are generated in each image/ video frame for higher accuracy. By relaxing the discrete non-convex set to its convex hull, the constraints that define the original set can now be separated from one image/ video to another. In the case of co-localizing videos, the constraints use the shortest-path algorithm to reach optimization.<ref name="Joulin" /> | |||
=== Traffic Assignment Problem === | === Traffic Assignment Problem === | ||
A typical transportation network, also known as flow network, is considered as a convex programming problem with linear constraints. With the vertices called nodes and the edges called arcs, a directed graph called a network is formed and the flow is monitored via the movement from one node, origin (O), to another node, destination (D) along the arc. The objective of this programming problem is to achieve user-equilibrium, which means system flow is set optimal without incurring unnecessarily high cost for users. | A typical transportation network, also known as flow network, is considered as a convex programming problem with linear constraints. With the vertices called nodes and the edges called arcs, a directed graph called a network is formed and the flow is monitored via the movement from one node, origin (O), to another node, destination (D) along the arc. The objective of this programming problem is to achieve user-equilibrium, which means system flow is set optimal without incurring unnecessarily high cost for users. | ||
The use of the Frank-Wolfe algorithm in this case means that the traffic assignment problem can be applied to nonlinear multicommodity network flow with flow dependent cost.<ref name="LeBlanc">LeBlanc, L., Morlok, E.K., & Pierskalla, W.P. (1975). An efficient approach to solving the road network equilibrium traffic assignment problem. ''Transportation Research'', 9, 309-318.</ref> The algorithm is also able to process a larger set of constraints with more O-D pairs. Since the Frank-Wolfe algorithm uses a descent method to search for the direction of extreme points, the technique only recognizes the sequence of the shortest route problems. Therefore, the Frank-Wolfe algorithm is known to solve the traffic assignment problem on networks with several hundred nodes efficiently with the minimal number of iterations. | The use of the Frank-Wolfe algorithm in this case means that the traffic assignment problem can be applied to nonlinear multicommodity network flow with flow dependent cost.<ref name="LeBlanc">LeBlanc, L., Morlok, E.K., & Pierskalla, W.P. (1975). [https://www.sciencedirect.com/science/article/abs/pii/0041164775900301 An efficient approach to solving the road network equilibrium traffic assignment problem.] ''Transportation Research'', 9, 309-318.</ref> The algorithm is also able to process a larger set of constraints with more O-D pairs. Since the Frank-Wolfe algorithm uses a descent method to search for the direction of extreme points, the technique only recognizes the sequence of the shortest route problems. Therefore, the Frank-Wolfe algorithm is known to solve the traffic assignment problem on networks with several hundred nodes efficiently with the minimal number of iterations. | ||
Due to the algorithm’s effectiveness in optimizing traffic assignment problem, it has been widely applied in many fields other than the estimation of the total demand for travel via road between a set of roads and zones. These applications include data-driven computer networks, fluids in pipes, currents in an electrical circuit and more. | Due to the algorithm’s effectiveness in optimizing traffic assignment problem, it has been widely applied in many fields other than the estimation of the total demand for travel via road between a set of roads and zones. These applications include data-driven computer networks, fluids in pipes, currents in an electrical circuit and more. | ||
=== Deep Neural Network Training === | === Deep Neural Network Training === | ||
Although [[Stochastic gradient descent|Stochastic Gradient Descent]] (SGD) is still the conventional machine learning technique for deep learning, the Frank-Wolfe algorithm has been proven to be applicable for training neural networks as well. Instead of taking projection steps via SGD, the | Although [[Stochastic gradient descent|Stochastic Gradient Descent]] (SGD) is still the conventional machine learning technique for deep learning, the Frank-Wolfe algorithm has been proven to be applicable for training neural networks as well. Instead of taking projection steps via SGD, the Frank-Wolfe algorithm adopts the simple projection-free first-order function by using the linear minimization oracle (LMO) approach for constrained optimization <ref name="Pokutta">Pokutta, S., Spiegel, C., & Zimmer, M. (2020). [https://arxiv.org/abs/2010.07243 Deep neural network training with Frank-Wolfe.] ''arXiv preprint arXiv:2010.07243''.</ref>: | ||
<math display=block>\theta_{t+1} = \theta_t + \alpha(\nu_t - \theta_t)</math> | <math display=block>\theta_{t+1} = \theta_t + \alpha(\nu_t - \theta_t)</math> | ||
| Line 59: | Line 213: | ||
with <math>\alpha \in</math> [0,1] and <math>\nu_t</math> being | with <math>\alpha \in</math> [0,1] and <math>\nu_t</math> being | ||
<math display=block>\nu_t = argmin_{\nu \in C} <\nabla L (\theta_t) , \nu></math> | <math display=block>\nu_t = argmin_{\nu \in C} <\nabla L (\theta_t) , \nu>.</math> | ||
Through LMO, non-unique solutions to the above equation that were deemed impossible by | Through LMO, non-unique solutions to the above equation that were deemed impossible by gradient-descent-based optimization would now be possible. In addition to the linearization approach, sparsity regularization is also applied to the scaling factors in the optimization of deep neural networks.<ref name="Huang">Huang, Z., and Wang, N. (2018). [https://doi.org/10.1007/978-3-030-01270-0_19 Data-driven sparse structure selection for deep neural networks.] ''Proceedings of the European conference on computer vision'' (pp.304-320). ECCV. </ref> By forcing some factors to zero, the highly complex computational process of training deep neural networks is simplified. Since the other major characteristics of Frank-Wolfe algorithm is describing solutions with sparse structures, deep neural network training benefits greatly from the application of this algorithm. | ||
== Conclusion == | == Conclusion == | ||
The Frank-Wolfe algorithm is one of the key techniques in the machine learning field. The algorithm features favor linear minimization, simple implementation, and low complexity. By using the simplex method that requires little alteration to the gradient and interpolation in each iteration, the optimization of the linearized quadratic objective function can be performed in a significantly shorter runtime and larger datasets can be processed more efficiently. Therefore, even though the convergence rate of Frank-Wolfe algorithm is slow due to the search for naive descent directions in each iteration, the benefits that the algorithm brings still outweigh the disadvantages. With the main characteristics of being projection-free and the capability of producing solutions for sparse structures, the algorithm gained popularity with many use cases in machine learning. | |||
== References == | == References == | ||
Latest revision as of 21:49, 15 December 2021
Author: Adeline Tse, Jeff Cheung, Tucker Barrett (SYSEN 5800 Fall 2021)
Introduction
The Frank-Wolfe algorithm is an iterative first-order optimization algorithm for constrained convex optimization, first proposed by Marguerite Frank and Philip Wolfe from Princeton University in 1956.[1] It is also known as the “gradient and interpolation” algorithm or sometimes the “conditional gradient method” as it utilizes a simplex method of comparing an initial feasible point with a secondary basic feasible point to maximize the linear constraints in each iteration, to find or approximate the optimal solution.
Advantages of the Frank-Wolfe algorithm include that it is simple to implement; it results in a projection-free computation (that is, it does not require projections back to the constraint set to ensure feasibility); and it generates solution iterations that are sparse with respect to the constraint set. However, one of the major drawbacks of Frank-Wolfe algorithm is its convergence in practical applications, which can potentially be a computationally intensive process. This has enabled research into new revisions and heuristics to accelerate the algorithm by better aligning the descent direction while still preserving the projection-free property. [2] Therefore, despite the downside of Frank-Wolfe algorithm, the numerous benefits of this algorithm allow it to be utilized in artificial intelligence, machine learning, traffic assignment, signal processing, and many more applications.
Theory & Methodology
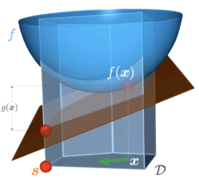
The Frank-Wolfe algorithm uses step size and postulated convexity, which formulates a matrix of positive semidefinite quadratic form. Just like a convex function yields a global minimum at any local minimum on a convex set, by the definition of nonlinear programming, the concave quadratic function would yield a global maximum point at any local maximum on a convex constraint set.
The methodology of the Frank-Wolfe algorithm starts with obtaining the generalized Lagrange multipliers for a quadratic problem, PI. The found multipliers are considered solutions to a new quadratic problem, PII. The simplex method is then applied to the new problem, PII, and the gradient and interpolation method is utilized to make incremental steps towards the solution of the original quadratic problem, PI. This is performed by taking an initial feasible point, obtaining a second basic feasible point along the gradient of the objective function at the initial point, and maximizing the objective function along the segment that joins these two points. The found maximum along the segment is utilized as the starting point for the next iteration.[1] Using this method, the values of the objective function converge to zero and in one of the iterations, a secondary point will yield a solution.
Proof
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} is a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [n \times 1]} matrix
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} is a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [m \times n]} matrix
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} is a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [n \times n]} matrix
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [1 \times n]} and matrices respectively
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla f(x)} is the gradient
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x) = \sum_{j=1}^n p_jx_j - \sum_{j,k=1}^{n,n} X_jC_{jk}X_k} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle where \; \sum_{j=1}^n A_{ij}X_j \le b_i \quad (i=1, ..., m) \; and \; X_j \ge 0 \quad (j = 1, ..., n)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla f(x) = \frac{df(x)}{dx}}
PI is represented by the following equations using matrix notation:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Maximize} \qquad f(x) = px' - x'Cx \quad \text{subject to}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (I) = \begin{cases} x \ge 0 \\ Ax \le b \end{cases}}
Since PI is feasible, any local maximum found that is contained within the convex constraint set is a global maximum. Then by utilizing Kuhn and Tucker's generalizations of the Lagrange Multipliers of the maximization of the objective function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0} is considered the solution of PI.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta f(x_0)x_0 = Max \, [ \, \delta f(x_0)w \, | \, w \ge 0, Aw \le b], \quad where \; w \; \text{is an} \; [n \times 1] \; \text{matrix}}
By the Duality Theorem, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Min \, [ \, ub \, | \, u \ge 0, \, uA \ge \delta f(x_o)], \quad where \; u \; \text{is a} \; [1 \times m] \; \text{matrix}}
Therefore, the solution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0} for PI is only valid if: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Max \, [ \, \delta f(x_0)x_0 - ub \, | \, u \ge 0, uA \ge \delta f(x_0)] = 0}
Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta f(x) = p - 2x'Cx} Therefore, by the generalization of Lagrangian, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x,u)} is extracted with linear constraints: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x,u) = \delta f(x)x - ub = px - ub - 2x'Cx} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} x \ge 0, \quad u \ge 0,\\ Ax \le b, \quad \delta f(x) \le uA \end{cases}}
The completion of the generalized Lagrangian shows that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m + n} positive variables exist for PI, thus a feasible solution exists.
Based on the concavity of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(y) - f(x) \le \delta f(x)(y-x)}
If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x,u)} satisfies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x,u) \le 0} (where x is a solution if for some Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u, \; g(x,u)=0} ), then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(y) - f(x) \le \delta f(x)x \le uAy - \delta f(x)x \le ub - \delta f(x)x = -g(x,u)}
By the Boundedness Criterion and the Approximation Criterion, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(y) - f(x) \le -g(x,u)}
The Frank-Wolfe algorithm then adds a non-negative variable to each of the inequalities to obtain the following:
- and are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [m \times 1]} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [n \times 1]} matrices respectively
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x, \, u, \, y, \, \nu \ge 0} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ax+y=b} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2Cx+A'u'-\nu '=p'} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x,u) = \delta f(x)x-ub = (uA-\nu )x-u(Ax+y) = - \nu x + uy}
Thus, the PII problem is to obtain search vectors to satisfy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu x+uy=0} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is considered a solution of PI if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta f(x)} belongs to the convex cone spanned by the outward normals to the bounding hyperplanes on which Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} lines as shown in Figure 1.
Algorithm
The Frank-Wolfe algorithm can generally be broken down into five steps as described below. Then the loop of iterations continues throughout Step 2 to Step 5 until the minimum extreme point is identified.
Step 1. Define initial solution
If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is the extreme point, the initial arbitrary basic feasible solution can be considered as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_k \in S \quad where \; k = 0}
The letter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} denotes the number of iterations.
Step 2. Determine search direction
Search direction, that is the direction vector is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_k = y_k - x_k}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_k} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_k} are feasible extreme points and belong to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} is convex
First-order Taylor expansion around Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_k} and problem is now reformulated to LP:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}min \quad & z_k(y) = f(x_k) + \nabla f(x_k)^T (y-x_k) \\ s.t. \quad & y \in S \\ \end{align}}
Step 3. Determine step length
Step size Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_k} is defined by the following formula where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_k} must be less than 1 to be feasible:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_k + \alpha_k p_k) < f(x_k)} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle min_{\alpha \in [0,1]} \, f(x_k + \alpha_k p_k)}
Step 4. Set new iteration point
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{k+1} = x_k + \alpha_k p_k}
Step 5. Stopping criterion
Check if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{k+1}} is an approximation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} , the extreme point. Otherwise, set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k = k + 1} and return to Step 2 for the next iteration.
In the Frank-Wolfe algorithm, the value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} descends after each iteration and eventually decreases towards Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} , the global minimum.
Numerical Example
Consider the non-linear problem below:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} min \quad &(x-1)^2 + (y-1)^2 \\ s.t. \quad & 2x+y \leq 6 \\ & x+2y \leq 6 \\ & x \geq 0 \\ & y \geq 0 \end{align}}
ITERATION 1
Step 1. Choose a starting point
Begin by choosing the feasible point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (0,0)} and take the partial derivatives of the objective function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta f_x(x,y) = 2(x-1)=2x-2 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta f_y(x,y) = 2(y-1)=2y-2 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \therefore \; \nabla f(0,0) = z_0 = [-2, -2] }
Step 2. Determine a search direction
Obtain the search direction by solving the linear problem that is subject to the constraints defined. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla f(0,0) \cdot (x,y)^T }
The solution of this linear problem is obtained via linear programming algorithm, which is the enumeration with the extreme points in the feasible region. Using the simplex method or an algebraic solver, the solution to linear problem is: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla f(0,0) \cdot (x,y)^T = (2,2)}
Thus, the direction vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_0} for this iteration Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_0 } is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} p_0 &= (x,y)^T - z_0 \\ &= [2,2] - [-2,-2] = [4, 4] \end{align}}
Step 3. Determine step length
Evaluate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_{\alpha_0} = f(4\alpha_0, 4\alpha_0)} to obtain step length Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_0} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \because \;\; \qquad f &=(4\alpha_0-1)^2 + (4\alpha_0-1)^2 \\ &= 32\alpha_0^2 -16\alpha_0 +2 \\ \nabla f(\alpha_0) &= 64\alpha_0 - 16 = 0 \\ \therefore \qquad \alpha_0 &= 16/64 = 1/4 \end{align}}
Step 4. Set new iteration point
The next point is determined by the following formula:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} x_1 &= x_0 + \alpha_0p_0 \\ &= [0,0] + 1/4 \cdot [4,4] \\ \therefore \; x_1 &= [1,1] \end{align} }
Step 5. Perform optimality test
If the following equation yields a zero, the optimal solution has been found for the problem. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} f_1 & = \nabla f(x_0) \cdot p_0 =\nabla f(0,0) \cdot p_0 \\ & = -2 \cdot 4 + -2 \cdot 4 = -16 \end{align}} Since the solution is not zero, the extreme point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0} is not optimal and another iteration is required.
ITERATION 2
Step 1. Utilize new iteration point as the starting point
From Step 4 in Iteration 1, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1 = [1,1]} . Therefore, substituting new iteration point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1} into Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta f_x(x,y)} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta f_y(x,y)} from Step 1, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla f(1,1) = z_1 = [0, 0] }
Since the gradient of the new starting point is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (0,0)} , the optimality test for the value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} will always yield Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_2 = \nabla f(1,1) \cdot p_1 = [0, 0] \cdot p_1}
Thus, the extreme point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1,1)} is the optimum solution for this non-linear problem.
Applications
Image and Video Co-localization

Co-localization is one of the programming methods in the machine learning field used to find a common object within a set of images or video frames. The process of co-localization involves first generating multiple candidate bounding boxes for each image/ video frame, then identifying the specific box in each image/ video frame that jointly contains the common object.[5] This technique is extremely important for analyzing online data. By being able to recognize the common objects, visual concepts can be tagged into specific labels, thus leveraging useful data for other marketing and product design purposes. Such development is especially useful for image and video hosting services such as Flickr and YouTube.
The formulation of co-localization using the Frank-Wolfe algorithm involves minimizing a standard quadratic programming problem and reducing it to a succession of simple linear integer problems. The benefit of the algorithm is that it allows many more images to be analyzed simultaneously and more bounding boxes are generated in each image/ video frame for higher accuracy. By relaxing the discrete non-convex set to its convex hull, the constraints that define the original set can now be separated from one image/ video to another. In the case of co-localizing videos, the constraints use the shortest-path algorithm to reach optimization.[4]
Traffic Assignment Problem
A typical transportation network, also known as flow network, is considered as a convex programming problem with linear constraints. With the vertices called nodes and the edges called arcs, a directed graph called a network is formed and the flow is monitored via the movement from one node, origin (O), to another node, destination (D) along the arc. The objective of this programming problem is to achieve user-equilibrium, which means system flow is set optimal without incurring unnecessarily high cost for users.
The use of the Frank-Wolfe algorithm in this case means that the traffic assignment problem can be applied to nonlinear multicommodity network flow with flow dependent cost.[6] The algorithm is also able to process a larger set of constraints with more O-D pairs. Since the Frank-Wolfe algorithm uses a descent method to search for the direction of extreme points, the technique only recognizes the sequence of the shortest route problems. Therefore, the Frank-Wolfe algorithm is known to solve the traffic assignment problem on networks with several hundred nodes efficiently with the minimal number of iterations.
Due to the algorithm’s effectiveness in optimizing traffic assignment problem, it has been widely applied in many fields other than the estimation of the total demand for travel via road between a set of roads and zones. These applications include data-driven computer networks, fluids in pipes, currents in an electrical circuit and more.
Deep Neural Network Training
Although Stochastic Gradient Descent (SGD) is still the conventional machine learning technique for deep learning, the Frank-Wolfe algorithm has been proven to be applicable for training neural networks as well. Instead of taking projection steps via SGD, the Frank-Wolfe algorithm adopts the simple projection-free first-order function by using the linear minimization oracle (LMO) approach for constrained optimization [7]:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_{t+1} = \theta_t + \alpha(\nu_t - \theta_t)}
with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha \in} [0,1] and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu_t} being
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu_t = argmin_{\nu \in C} <\nabla L (\theta_t) , \nu>.}
Through LMO, non-unique solutions to the above equation that were deemed impossible by gradient-descent-based optimization would now be possible. In addition to the linearization approach, sparsity regularization is also applied to the scaling factors in the optimization of deep neural networks.[8] By forcing some factors to zero, the highly complex computational process of training deep neural networks is simplified. Since the other major characteristics of Frank-Wolfe algorithm is describing solutions with sparse structures, deep neural network training benefits greatly from the application of this algorithm.
Conclusion
The Frank-Wolfe algorithm is one of the key techniques in the machine learning field. The algorithm features favor linear minimization, simple implementation, and low complexity. By using the simplex method that requires little alteration to the gradient and interpolation in each iteration, the optimization of the linearized quadratic objective function can be performed in a significantly shorter runtime and larger datasets can be processed more efficiently. Therefore, even though the convergence rate of Frank-Wolfe algorithm is slow due to the search for naive descent directions in each iteration, the benefits that the algorithm brings still outweigh the disadvantages. With the main characteristics of being projection-free and the capability of producing solutions for sparse structures, the algorithm gained popularity with many use cases in machine learning.
References
- ↑ 1.0 1.1 Frank, M. and Wolfe, P. (1956). An algorithm for quadratic programming. Naval Research Logistics Quarterly, 3(1-2):95–110.
- ↑ Combettes, C.W.. and Pokutta, S. (2020). Boosting Frank-Wolfe by chasing gradients. International Conference on Machine Learning (pp. 2111-2121). PMLR.
- ↑ Jaggi, M. (2013). Revisiting Frank-Wolfe: Projection-free sparse convex optimization. Inerational Conference on Machine Learning (pp.427-435). PMLR.
- ↑ 4.0 4.1 Joulin, A., Tang, K., & Li, F.F. (2014). Efficient image and video co-localization with frank-wolfe algorithm. European Conference on Computer Vision (pp. 253-268). Springer, Cham.
- ↑ Harzallah, H., Jurie, F., & Schmid, C. (2009). Combining efficient object localization and image classification. 2009 IEEE 12th international conference on computer vision (pp. 237-244). IEEE.
- ↑ LeBlanc, L., Morlok, E.K., & Pierskalla, W.P. (1975). An efficient approach to solving the road network equilibrium traffic assignment problem. Transportation Research, 9, 309-318.
- ↑ Pokutta, S., Spiegel, C., & Zimmer, M. (2020). Deep neural network training with Frank-Wolfe. arXiv preprint arXiv:2010.07243.
- ↑ Huang, Z., and Wang, N. (2018). Data-driven sparse structure selection for deep neural networks. Proceedings of the European conference on computer vision (pp.304-320). ECCV.
![{\displaystyle [1\times m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40df39f1cf3304969234e1835f02288e27e6599f)

