Interior-point method for NLP

Author: Apoorv Lal (CHEME 6800, Fall 2021)

Introduction

Interior point (IP) methods are used to solve all kind of problems from linear to non-linear, from convex to non convex. The first known IP method is Frisch's (1955) logarithmic barrier method that was later extensively studied by Fiacco and McCormick [5]. However, these methods mainly emerged in the late 1970's and 1980s. They were developed as algorithms to solve linear programming(LP) problems with a better worst case complexity than the simplex method [2]. In 1984, Karmarkar used IP methods to develop 'A new polynomial-Time method for Linear Programming' [3]. The main advantage of this method was better practical performance than the earlier algorithms like the ellipsoid method by Khachiyan [4]. After Karmarkar's publication more intensive research in this field led to development of a new category of IP methods known as 'primal-dual' methods. Currently, most powerful type of primal-dual codes are Ipopt, KNITRO and LOQO [2]. In recent years the majority of research in the field of IPs is for nonlinear optimisation problems, especially for second order (referred as SOCO) and semidefinite optimisation ( referred as SDO). SDO has wide range of applications in combinatorial optimization, control, structural engineering and electrical engineering [1].

Theory & Methodology

Nonlinear Constrained Optimisation

Equation set 1:General form for the nonlinear constrained optimisation problem

General form for any nonlinear constrained optimisation problem can be depicted as shown in Equation set 1.

• The objective function and constraints can be any linear, quadratic or any general nonlinear functions.
• Typically, applied for convex optimisation problems
• Convert maximisation problems to minimisation problems by taking negative of the objective function
• Convert any general inequalities to simple inequalities using slack variables.

Slack variables

Equation set 2: Constrained non linear optimisation problem without slack variables.

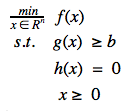
Consider a general equation of the form as shown in Equation set 2. Now we need to convert this form to the form as shown in Equation set 1. For this the inequality '$g(x)\geqslant b$ ' can be written $g(x)-b\geq 0$ which can be further written as:

$g(x)-b-s=0$ ,along with $s\geq 0$

Thus the set of equation '$g(x)-b-s=0$' and '$h(x)=0$' become '$c(x)=0$' as shown in Equation set 1.

Barrier function

Equation set 3: Objective function with barrier term

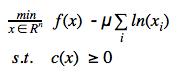
Once the given problem is converted to the standard form (as shown in Equation set 1), we will now try to remove the inequality constraint (x ≥ 0) using the barrier term. We will introduce natural log barrier term for inequality constraints as shown in Equation set 3. The point ln(x_i) is not defined for x_i ≤ 0. Our goal is to solve this barrier problem for a given 'μ' then decrease 'μ' and resolve the problem. If 'μ' is decreased at the right rate and the approximate solutions are good enough then this method will converge to an optimal solution of the non linear optimisation problem [1]. We want to only search in the interior feasible space.

Example for barrier function:

Example 1: Barrier function example

Figure 1: Variation of given objective function for different values of 'μ'

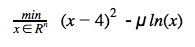
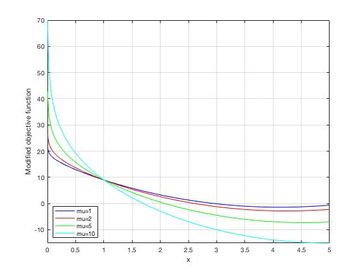
Example 1 shows how barrier term can be incorporated into the objective function. For different values of 'μ' , the value of objective function changes and thus as the value of 'μ' is decreased from '10' to '1' (as shown in Figure 1) , we approach towards the optimal solution i.e. x=4.

KKT Condition for Barrier Problem

KKT conditions for the barrier problem of the form

We can define

Numerical Example

Consider the following non-linear optimisation problem:

$\min x_{2}(5+x_{1})$

$s.t.x_{1}x_{2}\geq 5$

$x_{1}^{2}+{x_{2}}^{2}\leq 20$

This problem needs to be converted into standard form first:

$\min x_{2}(5+x_{1})$

$s.t.x_{1}x_{2}-5-x_{3}=0$

$-x_{1}^{2}-{x_{2}}^{2}-x4=0$

$c(x^{o})=$ ${\begin{bmatrix}-5\\20\end{bmatrix}}$

Applications

IP methods have proven computationally to be viable alternative for the solution of several power engineering optimisation models. A variety of these are applied to a number of power systems models. 'Optimal power flow (OPF)' seeks the operation point of a power system that maximizes a given objective function and satisfies operational and physical constraints. Given real-time operating conditions and the large scale of the power system, it is demanding to develop algorithms that allow for OPF to be decomposed and efficiently solved on parallel computing systems [6]. As compared to gradient based algorithms primal-dual based interior point methods have faster convergence rates.

A hydro-thermal coordination program deals with the problem of finding the scheduling and the production of every hydro and thermal plant of a system so that the customer demand is supplied at minimum cost with a certain level of security and all constraints related to the thermal and hydro subsystems are satisfied. A medium-term hydro-thermal coordination (MTHTC) problem results in a very large Non-Linear Mixed-Integer Programming problem [7]. IP optimisation codes are used to find the solution of these MTHTC problems.

IP methods are also used in Voltage collapse and reliability evaluation. Power flow unsolvability occurs when for a given set of active and reactive power loads the power flow equations have no real solution. This kind of problem may happen for instance when a heavily stressed system is subject to a severe contingency situation [8]. The set of control actions in the IP algorithm includes rescheduling of active power of generators, adjustments on terminal voltage of generators, tap changes on LTC transformers, and as a last resort, minimum load shedding [8].

Fuel Planning and Multi-reservoir management are some other areas where interior point methods have proven to be useful. A long-term fuel planning problem aims to minimize the sum of fuel purchase and yearly storage costs, subject to meeting the generation requirements, the constraints associatedwith fuel supply contracts, and the constraints associated with storage of fuel.

Conclusion

Interior Point methods remain an active and fruitful area of research, although the frenetic pace that has characterised the area slowed down in recent years. The infl􏰔uence on nonlinear programming theory and practice is yet to be determined􏰐 even though substantial research has already been done on this topic [10].

References

[1] Nonlinear Optimization, Immanuel M Bomze,Roger Fletcher...

[2] Martin Scmidt. An Interior Point Method for Nonlinear Optimization problems with locatable and separable non smoothness.

[3] Narendra Karmarkar. “A New Polynomial-Time Algorithm for Linear Programming.” In: Combinatorica 4.4 (1984), pp. 373–395. issn: 0209-9683. doi:10.1007/BF02579150.

[4] Leonid Genrikhovich Khachiyan. “A polynomial algorithm in linear program- ming.” In: Soviet Mathematics Doklady 20 (1979), pp. 191–194.

[5] Mevludin Glavic, Louis Wehenkel. Interior Point Methods: A Survey, Short Survey of Applications to Power Systems, and Research Opportunities. (2004)

[6] R. A. Jabr, A. H. Cooninck, B. J. Cory: ”A Primal-Dual Interior Point Method for Optimal Power Flow Dispatching”, IEEE Transactions on Power Systems, Vol. 17, No. 3, pp. 654-662, 2002.

[7] J. Medina, V. H. Quintana, A. J. Conejo, F. P. Thoden: “A Comparison of Interior-Point Codes for Medium-Term Hydro-Thermal Coordination”, IEEE PES Summer Meeting, Paper 0-7803-1/97, 1997.

[8] S. Grenville, J. C. O. Mello, A. C. G. Mello: “Application of interior point methods to power flow unsolvability”, IEEE Transactions on Power Systems, Vol. 11, pp. 1096-1103, 1996.

[9] V. R. Sherkat, Y. Ikura: “Experience with Interior Point Optimisation Software for a Fuel Planning Application” IEEE Transactions on Power Systems,Vol. 9, No. 2, 1994.

[10] Stephen J. Wright. "Recent developments in Interior point methods."