Interior-point method for NLP
Author: Apoorv Lal (CHEME 6800, Fall 2021)
Introduction
Interior point (IP) methods are used to solve all kind of problems from linear to non-linear, from convex to non convex. The first known IP method is Frisch's (1955) logarithmic barrier method that was later extensively studied by Fiacco and McCormick [1]. However, these methods mainly emerged in the late 1970's and 1980s. They were developed as algorithms to solve linear programming(LP) problems with a better worst case complexity than the simplex method [2]. In 1984, Karmarkar used IP methods to develop 'A new polynomial-Time method for Linear Programming' [3]. The main advantage of this method was better practical performance than the earlier algorithms like the ellipsoid method by Khachiyan [4]. After Karmarkar's publication more intensive research in this field led to development of a new category of IP methods known as 'primal-dual' methods. Currently, most powerful type of primal-dual codes are Ipopt, KNITRO and LOQO [5]. In recent years the majority of research in the field of IPs is for nonlinear optimisation problems, especially for second order (referred as SOCO) and semidefinite optimisation ( referred as SDO). SDO has wide range of applications in combinatorial optimization, control, structural engineering and electrical engineering [6].
Theory & Methodology
Nonlinear Constrained Optimisation
General form for any nonlinear constrained optimization problem can be depicted as shown in Equation set 1:
- The objective function and constraints can be any linear, quadratic or any general nonlinear functions.
- Typically, applied for convex optimization problems
- Convert maximisation problems to minimisation problems by taking negative of the objective function
- Convert any general inequalities to simple inequalities using slack variables.
Slack variables
Consider a general equation of the form as shown in Equation set 2:
Now we need to convert this form to the form as shown in Equation set 1. For this the inequality ' ' can be written which can be further written as:
, along with
Thus the set of equation '' and '' become '' as shown in Equation set 1.
Barrier function
Once the given problem is converted to the standard form (as shown in Equation set 1), we will now try to remove the inequality constraint using the barrier term. We will introduce natural log barrier term for inequality constraints as shown in Equation set 3:
The point is not defined for . Our goal is to solve this barrier problem for a given , then decrease this and resolve the problem. If is decreased at the right rate and the approximate solutions are good enough then this method will converge to an optimal solution of the non linear optimization problem. We want to only search in the interior feasible space.
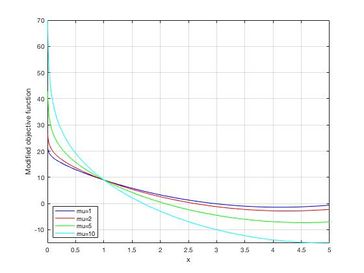
Example for barrier function:
Following example shows how barrier term can be incorporated into the objective function:
For different values of , the value of objective function changes and thus as the value of is decreased from '10' to '1' (as shown in Figure 1) , we approach towards the optimal solution i.e. .
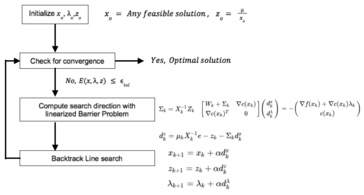
After we know the basics described above, the following methodology adopted from [7] can be used to solve the non-linear optimization problem.
KKT Condition for Barrier Problem
KKT conditions for the barrier problem of the form:
We can define now define and solve the modified version of the KKT conditions:
.
The matrix is simply a column vector of ones i.e. to satisfy the rules of matrix operations.
KKT solution with Newton-Raphson method
Here, , and are the search directions for the and is the second gradient of the Lagrangian.
Thus, and ,
The above system can be arranged into symmetric linear system as follows:
where
We can then solve for after finding the linear solution to and with the following form of the explicit solution:
Step size
After we have found out the search directions we need to find an appropriate value of the step size. The aim here is to find a value of step size to minimise the value of the objective functions and minimise the constraint violations. Following two methods are generally used to determine the value of :
- Decreasing the merit function: Merit function is defined as the sum of the objective function and the absolute values of the constraint violations multiplied by a scalar quantity i.e. so that it determines if it's a better step or not.
- Filter methods use a combination of objective function and constraint violations to determine whether to accept the step size or not.
Once the step size has been determined we can find out the values of
Convergence Criteria
Convergence criteria can be defined when KKT conditions are satisfied within a tolerance:
Pseudocode
The above described algorithm can be depicted in the form of the following pseudocode as illustrated by [8]
- Choose a feasible guess value of and initialise and by solving the above described equation.
- Once we have initial values then check for convergence, if it is within the 'tolerance limit' then we have reached the optimal solution. If not then, move to next step.
- Compute the search direction using the Equation(*) and Equation(**) as mentioned above.
- Perform back tracking line search by progressively decreasing the value of using merit function of Filter methods.
- Check for convergence again and repeat steps if the solution is not within tolerance limit.
Barrier method vs Primal-dual method
In order to understand the concept of central path and how the barrier method is different from primal-dual method, the following methodology adopted from [9] can be used:
Consider the simple case of an LP with the following form:
Primal problem:
Dual problem:
Assuming primal and dual problems are strictly feasible and
Central path : Set of points with with
is unique for all
The point is strictly primal feasible and satisfies:
with
is also strictly dual feasible: and
Duality gap between and can be calculated as:
The bound on the sub-optimality of :
, where is the optimal value of the LP.
The following overview on Barrier vs primal-dual method was given by [10]
- Both methods are motivated in terms of perturbed KKT conditions.
- Primal dual interior point methods take one Newton step and then move to next step i.e. there are no separate inner and outer loops.
- Primal dual interior point iterates are not necessarily feasible.
- Primal-dual interior-point methods are often more efficient, as they can exhibit better than linear convergence.
Numerical Example
Consider the following non-linear optimisation problem:
This problem needs to be converted into standard form first:
The initial guess values can be selected as
We will also choose the initial guess values of as .
, The first column represents and second column represents .
Now we will calculate the values of and at the initial guess values.
,
Now, . Similarly,
In the above equation Matrix and are basically diagonal matrices with the diagonal elements as follows:
and
As defined earlier, the matrix is simply a column vector of ones i.e.
Now since and we have chosen initial guess values of , thus .
Now we have everything to substitute in the following equation and calculate the search directions and iterate till we fulfil the convergence criteria:
We can now implement BPOPT solver using MATLAB to get the following results as illustrated by [11]:
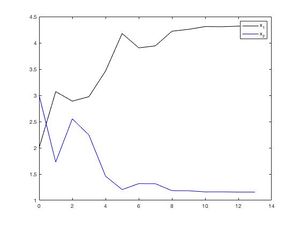
From figure 3 we see that the solver has converged to following optimal values of x1 and x2 in '13' iterations. and
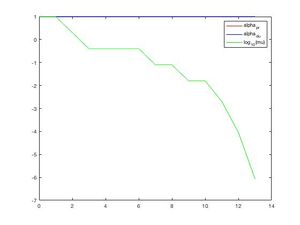
In the figure 4 we can clearly see how the value of is decreasing as we progress towards the solution (increasing iterations).
Applications
IP methods have proven computationally to be viable alternative for the solution of several power engineering optimisation models. A variety of these are applied to a number of power systems models. 'Optimal power flow (OPF)' seeks the operation point of a power system that maximizes a given objective function and satisfies operational and physical constraints. Given real-time operating conditions and the large scale of the power system, it is demanding to develop algorithms that allow for OPF to be decomposed and efficiently solved on parallel computing systems [12]. As compared to gradient based algorithms primal-dual based interior point methods have faster convergence rates.
A hydro-thermal coordination program deals with the problem of finding the scheduling and the production of every hydro and thermal plant of a system so that the customer demand is supplied at minimum cost with a certain level of security and all constraints related to the thermal and hydro subsystems are satisfied. A medium-term hydro-thermal coordination (MTHTC) problem results in a very large Non-Linear Mixed-Integer Programming problem [13] IP optimisation codes are used to find the solution of these MTHTC problems.
IP methods are also used in Voltage collapse and reliability evaluation. Power flow unsolvability occurs when for a given set of active and reactive power loads the power flow equations have no real solution. This kind of problem may happen for instance when a heavily stressed system is subject to a severe contingency situation. The set of control actions in the IP algorithm includes rescheduling of active power of generators, adjustments on terminal voltage of generators, tap changes on LTC transformers, and as a last resort, minimum load shedding [14].
Fuel Planning and Multi-reservoir management are some other areas where interior point methods have proven to be useful. A long-term fuel planning problem aims to minimize the sum of fuel purchase and yearly storage costs, subject to meeting the generation requirements, the constraints associatedwith fuel supply contracts, and the constraints associated with storage of fuel.[15]
Conclusion
Interior Point methods remain an active and fruitful area of research, although the frenetic pace that has characterized the area slowed down in recent years. Linear programming codes have become mainstream and continue to undergo development although they face stiff competition from the simplex method. Applications to quadratic programming show considerable promise, because of the superior ability of interior point approach to exploit problem structure efficiently. The influence on nonlinear programming theory and practice is yet to be determined even though substantial research has already been done on this topic [16]. An extensive evaluation of line search options was conducted by [17] and it was concluded that filter approach was the most robust approach. Many researchers are hopeful for the use of interior point approach in decomposition methods, though no rigorous comparative studies with alternative approaches have been performed.[18] Many authors have also worked on a special subclass of non smooth optimization problems and a new interior point method has been proposed for this class. These methods extend a standard interior-point method for nonlinear and nonconvex problems by additional line-search and step length computation features and a problem-tailored stationarity test. A special type of generalized gradients is developed that is used at points of the nonsmooth problems that fail to be differentiable.[19]
References
- ↑ Mevludin Glavic, Louis Wehenkel. Interior Point Methods: A Survey, Short Survey of Applications to Power Systems, and Research Opportunities. (2004)
- ↑ Martin Scmidt. An Interior Point Method for Nonlinear Optimization problems with locatable and separable non smoothness.
- ↑ Narendra Karmarkar. “A New Polynomial-Time Algorithm for Linear Programming.” In: Combinatorica 4.4 (1984), pp. 373–395. issn: 0209-9683. doi:10.1007/BF02579150.
- ↑ Leonid Genrikhovich Khachiyan. “A polynomial algorithm in linear program- ming.” In: Soviet Mathematics Doklady 20 (1979), pp. 191–194.
- ↑ Martin Scmidt. An Interior Point Method for Nonlinear Optimization problems with locatable and separable non smoothness.
- ↑ Bomze, Immanuel M., et al.Nonlinear Optimization, Springer-Verlag Berlin Heidelberg, 2010.
- ↑ A. Wächter and L. T. Biegler, On the Implementation of an Interior-Point Filter Line-Search Algorithm for Large-Scale Nonlinear Programming, Mathematical Programming 106(1), pp. 25-57, 2006.
- ↑ Interior point method for Optimization <https://www.youtube.com/watch?v=zm4mfr-QT1E>
- ↑ L.Vandenberghe."Lecture 13 The central path". <http://www.seas.ucla.edu/~vandenbe/ee236a/lectures/cpath.pdf>
- ↑ Ryan Tibshirani."Primal-Dual Interior-Point methods <https://www.stat.cmu.edu/~ryantibs/convexopt/lectures/primal-dual.pdf>
- ↑ Design Optimisation-Interior point methods, <https://apmonitor.com/me575/index.php/Main/InteriorPointMethod>
- ↑ R. A. Jabr, A. H. Cooninck, B. J. Cory: ”A Primal-Dual Interior Point Method for Optimal Power Flow Dispatching”, IEEE Transactions on Power Systems, Vol. 17, No. 3, pp. 654-662, 2002.
- ↑ J. Medina, V. H. Quintana, A. J. Conejo, F. P. Thoden: “A Comparison of Interior-Point Codes for Medium-Term Hydro-Thermal Coordination”, IEEE PES Summer Meeting, Paper 0-7803-1/97, 1997.
- ↑ S. Grenville, J. C. O. Mello, A. C. G. Mello: “Application of interior point methods to power flow unsolvability”, IEEE Transactions on Power Systems, Vol. 11, pp. 1096-1103, 1996.
- ↑ V. R. Sherkat, Y. Ikura: “Experience with Interior Point Optimisation Software for a Fuel Planning Application” IEEE Transactions on Power Systems,Vol. 9, No. 2, 1994.
- ↑ Stephen J. Wright. "Recent developments in Interior point methods."
- ↑ A. Wächter and L. T. Biegler, On the Implementation of an Interior-Point Filter Line-Search Algorithm for Large-Scale Nonlinear Programming, Mathematical Programming 106(1), pp. 25-57, 2006.
- ↑ Stephen J. Wright. "Recent developments in Interior point methods."
- ↑ Martin Scmidt. An Interior Point Method for Nonlinear Optimization problems with locatable and separable non smoothness.










































































































