Disjunctive inequalities

Authors: Derek Moore (drm323), Grant Logan (gsl59), Matthew Dinh (md992), Daniel Ladron (dl976)

Introduction

Disjunctive inequalities are a form of disjunctive constraints that can be applied to linear programming. Disjunctive constraints are applied in all disjunctive programming, which just refers to the use of logical constraints, which include the “Or” and “And” statements. In order to solve a disjunctive, the constraints have to be converted into multiple integer programming (MIP) constraints, which is called disjunction. Disjunction involves the implementation of a binary variable to create a new set of constraints that can be solved easily. Two common methods for disjunction are the Big-M Reformulation and the Convex-Hull Reformulation.

Method

General

When given a set of inequalities, such as $f_{1}(x)\ \leq \ 0\ \And \ f_{2}(x)\ \leq \ 0$, the disjunctive form is given by:  ${\begin{bmatrix}y\\f_{1}(x)\ \leq \ 0\end{bmatrix}}\lor {\begin{bmatrix}-y\\f_{2}(x)\ \leq \ 0\end{bmatrix}}$. In order to turn the problem into a solvable MIP or MILP, logical constraints are created by using sufficiently large numbers, such as M1 and M2, and a binary variable y for each inequality. This is shown below by M1, M2, y1, and y1:

$f_{1}(x)\ \leq \ M_{1}\ast (1-y_{1})$

$f_{2}(x)\ \leq \ M_{2}\ast (1-y_{2})$

To set the binary variable to be mutually exclusive, the sum of the variables is set to 1 and the range is set to {0,1}.

$y_{1}\ +y_{2}\ =\ 1$

$y_{1}\ ,\ y_{2}\epsilon \ {0,1}\ \$

Big-M Reformulation

Figure 1: Disjunctive inequality solution space that can be solved via disjunction using the Big-M Reformulation or the Convex-Hull Reformulation

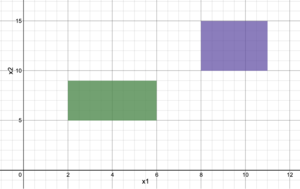
For the Big-M reformulation, a sufficiently large number, M, is used to nullify one set of constraints. This is accomplished by adding or subtracting the term “M*(1-y)” to the upper bound and lower bound constraints, respectively, with its respective binary variable. For example, given a solution space ${\begin{bmatrix}y\\2\leq \ x_{1}\ \leq 6\\5\leq \ x_{2}\ \leq 9\end{bmatrix}}\lor {\begin{bmatrix}-y\\8\leq \ x_{1}\ \leq 11\\10\leq \ x_{2}\ \leq 15\ \end{bmatrix}}$(shown graphically in Figure 1), to determine which of the solutions is optimal, the problem must be formulated such that one set of constraints is chosen. Using the Big-M Reformulation, the following MILP set would be obtained:

y Formulation

$2-M*(1-y_{1})\leq x1\leq 6+M*(1-y_{1})$

$5-M*(1-y_{1})\leq x2\leq 9+M*(1-y_{1})$

-y Formulation

$8-M*(1-y_{2})\leq x1\leq 11+M*(1-y_{2})$

$10-M*(1-y_{2})\leq x2\leq 15+M*(1-y_{2})$

Convex-Hull Reformulation

Similar to the Big-M reformulation, the convex-hull reformulation uses a binary variable, y, to constrain the set of inequalities. The first step in converting the problem into a solvable MILP is breaking all variables into a set of variables, such as (x1 → x11 + x12). By adding these addition variables, it is possible to isolate what set of parameters provide for the optimal solution of the problem. Then, similar to the Big-M reformulation, a sufficiently large variable, M, is used to nullify the non-optimal variable set, such as x11 and x12. For the problem show in Figure 1, the following variable constraints would be formulated:

y Formulation

$0\leq x_{11}\leq M*y_{1}$

$0\leq x_{21}\leq M*y_{1}$

-y Formulation

$0\leq x_{12}\leq M*y_{2}$

$0\leq x_{22}\leq M*y_{2}$

Formulation of the numerical constraints would then be implemented: y Formulation

$2\ast y_{1}\leq \ x_{11}\ \leq 6\ast y_{1}$

$5\ast y1\leq \ x_{21}\ \leq 9\ast y1$

-y Formulation

$8\ast y_{2}\leq \ x_{12}\ \leq 11\ast y_{2}$

$10\ast y_{2}\leq \ x_{22}\ \leq 15\ast y_{2}$

With the Convex-Hull transformation, the additional constraints confine the problem, such that a tighter (convex) solution space is examined compared to Big-M Formulation.

Examples

A good example of solving a disjunctive inequalities is using the reformulation methods below:

$[x1-x2\leq -1]V[-x1+x2\leq -1]$

$0\leq x1\leq 4,0\leq x2\leq 4$

Using Big-M Formulation:

$x1-x2\leq -1+M(1-y1)$

$-x1+x2\leq -1+M(1-y2)$

$y1+y2=1,y1,y2=0,1$

$0\leq x1\leq 4,0\leq x2\leq 4,M=10$

Using Convex-hull Formulation:

$x1=z11+z12,x2=z21+z22$

$z11-z12\leq -y1,-z12-z12\leq -y1$

$1=y1+y2,y1,y2=0,1$

$0\leq z11\leq 4y1,0\leq z12\leq 4y2$

$0\leq z21\leq 4y1,0\leq z22\leq 4y2$

Applications

Applying Big-M Method

If an Linear Programing has any constraints either > or =, a starting basic feasible solution may not be achieved. By adding "artificial" variables to the problem, the Big-M method helps draw to a finite conclusion. By modifying the original Linear Programing with the new 'artificial" variable it ensures they are all equal to 0 at the end of the simplex algorithm.

Steps

1. Modifying the constraints so that the Right Hand Side of each constraint is non-negative. Remember that if a inequality is multiplied by a negative number the direction if the inequality is reversed. After this modification, identify each constraint as <, >, or =.

2. Converting each inequality constraint to standard form (If constraint $i$ is a < constraint, we add a slack variable $s_{i}$; and if constraint $i$ is a > constraint, we subtract an excess variable $e_{i}$).

3. Adding an artificial variable $a_{i}$ to the constraints identified as > or = constraints at the end of Step 1. Also add the sign restriction $a_{i}$ > 0.

4. If the Linear Programming is a max problem, add (for each artificial variable) $-Ma_{i}$ to the objective function where M denotes a very large positive number.

5. If the Linear Programming is a min problem, add (for each artificial variable) $Ma_{i}$ to the objective function.

6. Solving the transformed problem with the simplex . Since each artificial variable will be in the starting basis, all artificial variables must be eliminated from row 0 before beginning the simplex. Now (In choosing the entering variable, remember that M is a very large positive number!).

If all artificial variables are equal to zero in the optimal solution, we have found the optimal solution to the original problem.

If any artificial variables are positive in the optimal solution, the original problem is infeasible

Conclusion

Disjunctive inequalities can be used to generate all valid inequalities for an integer program. A simple disjunctive procedure can be used to generate all valid inequalities for a 0 or 1 mixed integer program. It could be shown that to obtain the convex hull of a 0 or 1 mixed integer program, it suffices to take the convex hull of each 0 or 1 variable at a time. Another method to reformulate a disjunctive inequality is to implement the Big-M method which generates a much smaller MILP/MINLP with a tighter relaxation than the convex-hull method.