Disjunctive inequalities
Authors: Derek Moore, Grant Logan, Matthew Dinh, Daniel Ladron (SYSEN 5800/CHEME 6800 Fall 2021)
Introduction
Disjunctive inequalities are a form of disjunctive constraints that can be applied to linear programming. Disjunctive constraints are applied in all disjunctive programming, which just refers to the use of logical constraints in linear inequalities, which include “Or", ”And", or "Complement of" statements.[1] In order to solve a disjunctive, the constraints have to be converted into mixed-integer programming (MIP) or mixed-inter linear programming (MILP) constraints, which is called disjunction. Disjunction involves the implementation of a binary variable to create a new set of constraints that can be solved easily. Two common methods for disjunction are the Big-M Reformulation and the Convex-Hull Reformulation.[2]
Method
General
When given a set of inequalities, such as , the disjunctive form is given by: [1] In order to turn the problem into a solvable MIP or MILP, logical constraints are created by using sufficiently large numbers, such as and , and a binary variable y for each inequality. This is shown below by , , and :
To set the binary variable to be mutually exclusive, the sum of the variables is set to 1 and the range is set to {0,1}.
Big-M Reformulation[1][2]
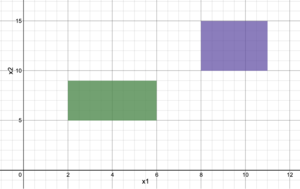
For the Big-M reformulation, a sufficiently large number, , is used to nullify one set of constraints. This is accomplished by adding or subtracting the term “” to the upper bound and lower bound constraints, respectively, with its respective binary variable. While choosing a large M value allows for isolation, the large value also yields poor relaxation of the model space.[3]
For example, given a solution space (shown graphically in Figure 1), to determine which of the solutions is optimal, the problem must be formulated such that one set of constraints is chosen. Using the Big-M Reformulation, the following MILP set would be obtained:
Formulation
Formulation
Convex-Hull Reformulation[1][2]
Similar to the Big-M reformulation, the convex-hull reformulation uses a binary variable, y, to constrain the set of inequalities. The first step in converting the problem into a solvable MILP is breaking all variables into a set of variables, such as ( → + ). By adding these addition variables, it is possible to isolate what set of parameters provide for the optimal solution of the problem. Then, similar to the Big-M reformulation, a sufficiently large variable, M, is used to nullify the non-optimal variable set, such as and . For the problem show in Figure 1, the following variable constraints would be formulated:
Formulation
Formulation
Formulation of the numerical constraints would then be implemented:
Formulation
Formulation
With the Convex-Hull transformation, the additional constraints confine the problem, such that a tighter (convex) solution space is examined compared to Big-M Formulation.[3]
Numerical Example
Given the following Disjunctive Inequality form below, reformulate the following problem using Convex Hull method and Big-M:
Convex Hull Method
We begin by setting introducing a binary variable y as a summation to 1:
{0,1}
Next we begin by grouping our values.
Next nullify the non-optimal variable sets with another binary variable large variable to:
Keep in mind the must be sufficiently large, too large of a value can yield to poor relaxation of the LP.
Finally the below constraints are reformulated from the original constraints, reformulated with included to pin when , subject to the original constraint when .
The reformulated constraint set is thus all of these constraints, making the problem a MIP.
Big-M Method
We now present the same constraint set reformulated by the Big-M method. We can begin by setting 2 binary variables and summing to 1.
{0,1}
Next, we add the binary variable as it is a arbitrarily large constant which is used to reformulate the inequality. Each inequality is formed in a single step by adding or subtracting depending on if the inequality is greater than or equal to, or less than or equal to.
In this way, if and the first set of inequalities is enforced and the second set of inequalities are dramatically expanded, effectively keeping them from constraining the problem, given that is large enough.
Applications
Disjunctive inequality programming can be used to solve real world problems in various sectors. Integer programming formulations utilizing a binary decision variable on which multiple constraints depend can be reformulated into disjunctive inequality formulations.
Strip Packing Problem
The Strip Packing Problem is a well-known problem in which two dimensional rectangles, or strips, are aligned in a two dimensional grid, subject to the constraints that the strips do not overlap. One method of formulating this problem is to describe the non-overlapping constraints as a set of four statements: for an existing rectangle , a new rectangle must be above, below, to the left, or to the right of rectangle . Each situation represents a unique inequality constraint; for example, if is above , then it must hold that the lower border of is at a greater value than the lower border of plus the height of . This can be extended to remove symmetries and improve efficiency of the solutions as well[4]. This can also be extended into three dimensions, for applications such as loading a cargo ship.
Process Scheduling
Disjunctive inequalities are invaluable for decisions within process engineering when multiple setups, reactors, or processes are possible. In process scheduling, machine and shop floor operations are scheduled in such a way to maximize production of a final product, minimize downtime, or maximize profit. Many of the decisions underlying these operations are binary: whether or not to run a machine/operation at a given time. If a machine/operation is run, constraints are required to define costs (CAPEX and OPEX), profits, thermodynamic constraints, and resources (including mass and energy balances) associated with the running machine/operation. If a machine/operation is not run, a different set of constraints is required to define idle costs and resources. This can be formulated into a disjunctive inequality formulation and solved using the described methods. The disjunctive inequality takes the form:
In this general formulation, represents the cost of enforcing a term, continuous variables represent system parameters, and constraints represent thermodynamic and resource constraints as described above [5]. Some specific applications include distillation columns, pharmaceutical purification plants, and wastewater treatment plants.
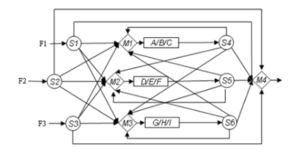
Figure 2 shows a special case of process scheduling, a wastewater network that removes pollutants from its mixture. The task is to figure out the total cost to discharge the pollution.[6] This wastewater system can be reformulated into a non-convex General Disjunction Programming problem shown below:[6]
{True, False}
Conclusion
As shown, disjunctive inequalities can be used to formulate various different types of mixed-integer program linear and nonlinear programs where binary decisions determine constraint sets. Two methods that are used to reformulate the problem are Convex Hull and Big-M reformulations. It could be shown that to obtain the convex hull of a 0 or 1 mixed-integer program, it suffices to take the convex hull of each 0 or 1 variable at a time [3]. Implementing the Big-M method generates a much smaller MILP/MINLP with a tighter relaxation than the convex-hull method, providing more efficient computational solutions. Disjunctive inequalities can also be used to improve the performance of any general purpose Branch-and-Cut algorithm as shown on the research from Balas and Bonami [7]. Many of the real world problems that can be solved through disjunctive inequalities involve process optimization where various binary decisions have to be made to optimize the solution. Examples of real world problems illustrated here include cargo packing and processing plants such as wastewater treatment plants. In conclusion, formulating these types of problems with disjunctive inequalities allows for a simple representation and conversion to MILP/MILP, solvable with standard MILP/MINLP solution algorithms.
References
- ↑ 1.0 1.1 1.2 1.3 E. Balas, “Disjunctive programming,” Annals of Discr. Math., vol. 5, pp. 6-11, 1979.
- ↑ 2.0 2.1 2.2 Pedro M. Castro and Ignacio E. Grossmann. 'Generalized Disjunctive Programming as a Systematic Modeling Framework to Derive Scheduling Formulations." 2012 51 (16), 5781-5792 DOI: 10.1021/ie2030486
- ↑ 3.0 3.1 3.2 You, Fengqi. (2021). "Mixed-Integer Linear Programming."
- ↑ Trespalacios, Francisco, and Ignacio E. Grossmann. "Symmetry breaking for generalized disjunctive programming formulation of the strip packing problem." Annals of Operations Research 258, no. 2 (2017): 747-759.
- ↑ Grossmann, Ignacio E., and Francisco Trespalacios. "Systematic modeling of discrete‐continuous optimization models through generalized disjunctive programming." AIChE Journal 59, no. 9 (2013): 3276-3295.
- ↑ 6.0 6.1 Grossmann, Ignacio E., and Juan P. Ruiz. Generalized Disjunctive Programming: A framework for formulation and alternative algorithms for MINLP optimization, Mixed Integer Nonlinear Programming, Springer New York, 2012.
- ↑ E. Balas, P. Bonami. "Generating lift-and-project cuts from the LP simplex tableau: open source implementation and testing of new variants. Math. Prog. Comp. 1", 165–199 (2009)




















































































