Adam: Difference between revisions

From Cornell University Computational Optimization Open Textbook - Optimization Wiki
Jump to navigation Jump to search
VisualWikitext
No edit summary
No edit summary
Line 4: Line 4:
Adam optimizer is the extended version of stochastic gradient descent which has broader scope in future for deep learning applications in computer vision and natural processing. It is an optimization algorithm that can be an alternative for stochastic gradient descent process. The name is derived from adaptive moment estimation. Adam is proposed as the most efficient stochastic optimization which only requires first order gradients where memory requirement too less.<ref>https://arxiv.org/pdf/1412.6980.pdf ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION</ref> Before Adam many adaptive optimization techniques were introduced such as AdaGrad, RMSP which have good performance over SGD but in some cases have some disadvantages such as generalizing performance which is worse than that of the SGD in some cases. So Adam was introduced which is better in terms of generalizing performance.
Adam optimizer is the extended version of stochastic gradient descent which has broader scope in future for deep learning applications in computer vision and natural processing. It is an optimization algorithm that can be an alternative for stochastic gradient descent process. The name is derived from adaptive moment estimation. Adam is proposed as the most efficient stochastic optimization which only requires first order gradients where memory requirement too less.<ref>https://arxiv.org/pdf/1412.6980.pdf ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION</ref> Before Adam many adaptive optimization techniques were introduced such as AdaGrad, RMSP which have good performance over SGD but in some cases have some disadvantages such as generalizing performance which is worse than that of the SGD in some cases. So Adam was introduced which is better in terms of generalizing performance.


== Background ==
== Theory ==
=== Batch Gradient Descent ===
Adam is a combination of two gradient descent methods which are explained below,
In standard batch gradient descent, the parameters, <math>\theta</math>, of the objective function <math>f(\theta)</math>, are updated based on the gradient of <math>f</math> with respect to
<math>\theta</math> for the entire training dataset, as
<math> g_t =\nabla_{\theta_{t-1}} f \big(\theta_{t-1} \big) </math> <br/>
<math> \theta_t = \theta_{t-1} - \alpha g_t , </math> <br/>


where <math>\alpha</math> is defined as the learning rate and is a hyper-parameter of the optimization algorithm, and <math>t</math> is the iteration number. Key challenges of the standard gradient descent method are the tendency to get stuck in local minima and/or saddle points of the objective function, as well as choosing a proper learning rate, <math>\alpha</math>, which can lead to poor convergence.<ref>Ruder, Sebastian. An Overview of Gradient Descent Optimization Algorithms, 2016, pp. 1–14, http://arxiv.org/abs/1609.04747.</ref>
=== Momentum: ===
This is a optimization algorithm which takes into consideration the 'exponentially weighted average' and accelerates the gradient descent. It is an extension of gradient descent optimization algorithm. The Momentum algorithm is solved in two parts. First is to calculate the change to position and second one is to update the old position with the updated position. The change in position is given by,
update = α * m_t
The new position or weights at time t is given by,
w_t+1 = w_t - update
Here in the above equation α(Step Size) is the Hyperparameter which controls the movement in the search space which is also called as learning rate. And,f'(x) is the derivative function or aggregate of gradients at time t.
where,
mt = β * m_t - 1 + (1 - β) * (∂L / ∂w_t)
In the above equations m_t and m_t-1 are aggregate of gradients at time t and aggregate of gradient at time t-1.
According to <ref>Deep Learning (Adaptive Computation and Machine Learning series)</ref> Momentum has the effect of dampening down the change in the gradient and, in turn, the step size with each new point in the search space.


=== Stochastic Gradient Descent ===
=== Stochastic Gradient Descent ===

Revision as of 15:29, 29 November 2021

Author: Akash Ajagekar (SYSEN 6800 Fall 2021)

Introduction

Adam optimizer is the extended version of stochastic gradient descent which has broader scope in future for deep learning applications in computer vision and natural processing. It is an optimization algorithm that can be an alternative for stochastic gradient descent process. The name is derived from adaptive moment estimation. Adam is proposed as the most efficient stochastic optimization which only requires first order gradients where memory requirement too less.[1] Before Adam many adaptive optimization techniques were introduced such as AdaGrad, RMSP which have good performance over SGD but in some cases have some disadvantages such as generalizing performance which is worse than that of the SGD in some cases. So Adam was introduced which is better in terms of generalizing performance.

Theory

Adam is a combination of two gradient descent methods which are explained below,

Momentum:

This is a optimization algorithm which takes into consideration the 'exponentially weighted average' and accelerates the gradient descent. It is an extension of gradient descent optimization algorithm. The Momentum algorithm is solved in two parts. First is to calculate the change to position and second one is to update the old position with the updated position. The change in position is given by, 

update = α * m_t

The new position or weights at time t is given by, w_t+1 = w_t - update Here in the above equation α(Step Size) is the Hyperparameter which controls the movement in the search space which is also called as learning rate. And,f'(x) is the derivative function or aggregate of gradients at time t. where, mt = β * m_t - 1 + (1 - β) * (∂L / ∂w_t) In the above equations m_t and m_t-1 are aggregate of gradients at time t and aggregate of gradient at time t-1. According to [2] Momentum has the effect of dampening down the change in the gradient and, in turn, the step size with each new point in the search space.

Stochastic Gradient Descent

Another variant of gradient descent is stochastic gradient descent (SGD), the gradient is computed and parameters are updated as in equation 1, but for each training sample in the training set.

Mini-Batch Gradient Descent

In between batch gradient descent and stochastic gradient descent, mini-batch gradient descent computes parameters updates on the gradient computed from a subset of the training set, where the size of the subset is often referred to as the batch size.

Adam Algorithm

The Adam algorithm first computes the gradient, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_t} of the objective function with respect to the parameters Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} , but then computes and stores first and second order moments of the gradient, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_t} respectively, as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_t = \beta_1 \cdot m_{t-1} + (1-\beta_1) \cdot g_t }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_t = \beta_2 \cdot v_{t-1} + (1-\beta_2) \cdot g_t^2, }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_2} are hyper-parameters that are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \in [0,1]} . These parameters can seen as exponential decay rates of the estimated moments, as the previous value is successively multiplied by the value less than 1 in each iteration. The authors of the original paper suggest values Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_1 = 0.9} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_2 = 0.999} . In the current notation, the first iteration of the algorithm is at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t=1} and both, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_0} are initialized to zero. Since both moments are initialized to zero, at early time steps, these values are biased towards zero. To counter this, the authors proposed a corrected update to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_t} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_t} as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{m}_t = m_t / (1-\beta_1 ^t) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{v}_t = v_t / (1-\beta_2 ^t). }
Finally, the parameter update is computed as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_t = \theta_{t-1} - \alpha \cdot \hat{m}_t / (\sqrt{\hat{v}_t} + \epsilon), }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} is a small constant for stability. The authors recommend a value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon=10^{-8}} .

Numerical Example

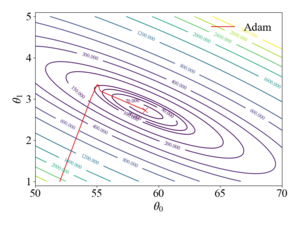
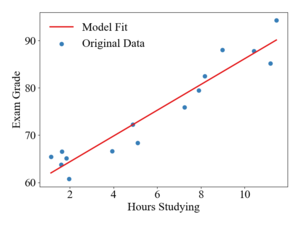
Contour plot of the loss function showing the trajectory of Adam algorithm from the initial point
Plot showing original data points and resulting model fit from the Adam algorithm


To illustrate how updates occur in the Adam algorithm, consider a linear, least-squares regression problem formulation. The table below shows a sample data-set of student exam grades and the number of hours spent studying for the exam. The goal of this example will be to generate a linear model to predict exam grades as a function of time spent studying.

Hours Studying 9.0 4.9 1.6 1.9 7.9 2.0 11.5 3.9 1.1 1.6 5.1 8.2 7.3 10.4 11.2
Exam Grad 88.0 72.3 66.5 65.1 79.5 60.8 94.3, 66.7 65.4 63.8 68.4 82.5 75.9 87.8 85.2

The hypothesized model function will be

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_\theta(x) = \theta_0 + \theta_1 x.}

The cost function is defined as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J({\theta}) = \frac{1}{2}\sum_i^n \big(f_\theta(x_i) - y_i \big)^2, }

Where the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/2} coefficient is used only to make the derivatives cleaner. The optimization problem can then be formulated as trying to find the values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} that minimize the squared residuals of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_\theta(x)} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} .

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{argmin}_{\theta} \quad \frac{1}{n}\sum_{i}^n \big(f_\theta(x_i) - y_i \big) ^2 }

For simplicity, parameters will be updated after every data point i.e. a batch size of 1. For a single data point the derivatives of the cost function with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_1} are

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial J(\theta)}{\partial \theta_0} = \big(f_\theta(x) - y \big) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial J(\theta)}{\partial \theta_1} = \big(f_\theta(x) - y \big) x }

The initial values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\theta}} will be set to [50, 1] and The learning rate, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} , is set to 0.1 and the suggested parameters for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_1} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_2} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} are used. With the first data sample of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x,y)=[8.98, 88.01]} , the computed gradients are

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial J(\theta)}{\partial \theta_0} = \big((50 + 1\cdot 9 - 88.01 \big) = -29.0 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial J(\theta)}{\partial \theta_1} = \big((50 + 1\cdot 9 - 88.01 \big)\cdot 9.0 = -261 }

With Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_0} being initialized to zero, the calculations of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_1} are

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_1 = 0.9 \cdot 0 + (1-0.9) \cdot \begin{bmatrix} -29\\ -261 \end{bmatrix} = \begin{bmatrix} -2.9\\ -26.1\end{bmatrix} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_1 = 0.999\cdot 0 + (1-0.999) \cdot \begin{bmatrix} -29^2\\-261^2 \end{bmatrix} = \begin{bmatrix} 0.84\\ 68.2\end{bmatrix} , }

The bias-corrected terms are computed as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{m}_1 = \begin{bmatrix} -2.9\\ -26.1\end{bmatrix} \frac{1}{ (1-0.9^1)} = \begin{bmatrix} -29.0\\-261.1\end{bmatrix}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{v}_1 = \begin{bmatrix} 0.84\\ 68.2\end{bmatrix} \frac{1} {(1-0.999^1)} = \begin{bmatrix} 851.5\\68168\end{bmatrix}. }

Finally, the parameter update is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_0 = 50 - 0.1 \cdot -29 / (\sqrt{851.5} + 10^{-8}) = 50.1 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_1 = 1 - 0.1 \cdot -261 / (\sqrt{68168} + 10^{-8}) = 1.1 }

This procedure is repeated until the parameters have converged, giving Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} values of . The figures to the right show the trajectory of the Adam algorithm over a contour plot of the objective function and the resulting model fit. It should be noted that the stochastic gradient descent algorithm with a learning rate of 0.1 diverges and with a rate of 0.01, SGD oscillates around the global minimum due to the large magnitudes of the gradient in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_1} direction.


Applications

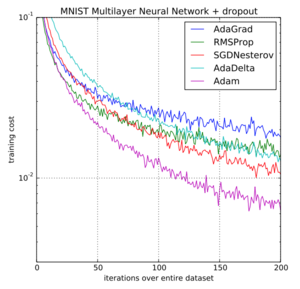
Comparison of training a multilayer neural network on MNIST images for different gradient descent algorithms published in the original Adam paper (Kingma, 2015)[3].

The Adam optimization algorithm has been widely used in machine learning applications to train model parameters. When used with backpropagation, the Adam algorithm has been shown to be a very robust and efficient method for training artificial neural networks and is capable of working well with a variety of structures and applications. In their original paper, the authors present three different training examples, logistic regression, multi-layer neural networks for classification of MNIST images, and a convolutional neural network (CNN). The training results from the original Adam paper showing the objective function cost vs. the iteration over the entire data set for the multi-layer neural network is shown to the right.

Variants of Adam

AdaMax

AdaMax[3] is a variant of the Adam algorithm proposed in the original Adam paper that uses an exponentially weighted infinity norm instead of the second-order moment estimate. The weighted infinity norm updated Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_t} , is computed as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_t = \max(\beta_2 \cdot u_{t-1}, |g_t|). }

The parameter update then becomes

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_t = \theta_{t-1} - (\alpha / (1-\beta_1^t)) \cdot m_t / u_t. }

Nadam

The Nadam algorithm[4] was proposed in 2016 and incorporates the Nesterov Accelerate Gradient (NAG)[5], a popular momentum like SGD variation, into the first-order moment term.

Conclusion

Adam is a variant of the gradient descent algorithm that has been widely adopted in the machine learning community. Adam can be seen as the combination of two other variants of gradient descent, SGD with momentum and RMSProp. Adam uses estimations of the first and second-order moments of the gradient to adapt the parameter update. These moment estimations are computed via moving averages,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_t} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_t} , of the gradient and the squared gradient respectfully. In a variety of neural network training applications, Adam has shown increased convergence and robustness over other gradient descent algorithms and is often recommended as the default optimizer for training.[6]

References

  1. ↑ https://arxiv.org/pdf/1412.6980.pdf ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION
  2. ↑ Deep Learning (Adaptive Computation and Machine Learning series)
  3. ↑ 3.0 3.1 Cite error: Invalid <ref> tag; no text was provided for refs named adam
  4. ↑ Dozat, Timothy. Incorporating Nesterov Momentum into Adam. ICLR Workshop, no. 1, 2016, pp. 2013–16.
  5. ↑ Nesterov, Yuri. A method of solving a convex programming problem with convergence rate O(1/k^2). In Soviet Mathematics Doklady, 1983, pp. 372-376.
  6. ↑ "Neural Networks Part 3: Learning and Evaluation," CS231n: Convolutional Neural Networks for Visual Recognition, Stanford Unversity, 2020
Retrieved from "https://optimization.cbe.cornell.edu/index.php?title=Adam&oldid=4603"