Adam
Author: Akash Ajagekar (SYSEN 6800 Fall 2021)
Introduction
Adam optimizer is the extended version of stochastic gradient descent which could be implemented in various deep learning applications such as computer vision and natural language processing in the future years. Adam was first introduced in 2014. It was first presented at a famous conference for deep learning researchers called ICLR 2015. It is an optimization algorithm that can be an alternative for the stochastic gradient descent process. The name is derived from adaptive moment estimation. The optimizer is called Adam because uses estimations of the first and second moments of the gradient to adapt the learning rate for each weight of the neural network. The name of the optimizer is Adam; it is not an acronym. Adam is proposed as the most efficient stochastic optimization which only requires first-order gradients where memory requirement is too little. Before Adam, many adaptive optimization techniques were introduced such as AdaGrad, RMSP which have good performance over SGD but in some cases have some disadvantages such as generalizing performance which is worse than that of the SGD in some cases. So, Adam was introduced which is better in terms of generalizing performance. Also in Adam, the hyperparameters have intuitive interpretations and hence required less tuning.[1] Adam performs well. But in some cases, researchers have observed Adam doesn't converge to the optimal solution, SGD optimizer does instead. In a diverse set of deep learning tasks sometimes Adam optimizers have low generalizing performance. According to the author Nitish Shirish Keskar and Richard Socher, switching to SGD in some cases show better generalizing performance than Adam alone.[2]
Theory
In Adam instead of adapting learning rates based on the average first moment as in RMSP, Adam makes use of the average of the second moments of the gradients. Adam. This algorithm calculates the exponential moving average of gradients and square gradients. And the parameters of β1 and β2 are used to control the decay rates of these moving averages. Adam is a combination of two gradient descent methods, Momentum, and RMSP which are explained below.
Momentum:
This is an optimization algorithm that takes into consideration the 'exponentially weighted average' and accelerates the gradient descent. It is an extension of the gradient descent optimization algorithm.[3]
The Momentum algorithm is solved in two parts. The first is to calculate the position change and the second is to update the old position. The change in the position is given by;
The new position or weights at time t is given by;
Here in the above equation is the Hyperparameter which controls the movement in the search space which is also called as learning rate. And, is the derivative function or aggregate of gradients at time t.
where;
In the above equations and are aggregate of gradients at time t and aggregate of gradient at time t-1.
Momentum has the effect of dampening down the change in the gradient and, in turn, the step size with each new point in the search space.
Root Mean Square Propagation (RMSP):
RMSP is an adaptive optimization algorithm that is an improved version of AdaGrad. RMSP tackles to solve the problems of momentum and works well in online settings. [4] In AdaGrad we take the cumulative summation of squared gradients but, in RMSP we take the 'exponential average'.
It is given by,
where,
Here,
Aggregate of gradient at t =
Aggregate of gradient at t - 1 =
Weights at time t =
Weights at time t + 1 =
= learning rate(Hyperparameter)
∂L = derivative of loss function
∂w_t = derivative of weights at t
β = Average parameter
= constant
But as we know these two optimizers explained below have some problems such as generalizing performance. The article [5] tells us that Adam takes over the attributes of the above two optimizers and builds upon them to give more optimized gradient descent.
Algorithm
Taking the equations used in the above two optimizers;
and
Initially, both mt and vt are set to 0. Both tend to be more biased towards 0 as β1 and β2 are equal to 1. By computing bias-corrected and , this problem is corrected by the Adam optimizer. The equations are as follows;
Now as we are getting used to gradient descent after every iteration and hence it remains controlled and unbiased. Now substitute the new parameters in place of the old ones. We get;
The pseudocode for the Adam optimizer is given below;
while w(t) not converged do
end
return w(t)
Performance
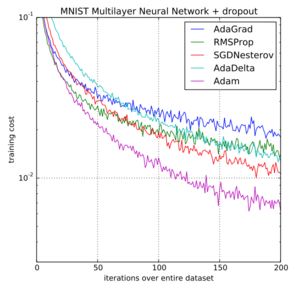
Adam optimizer gives much higher performance results than the other optimizers and outperforms by a big margin for a better-optimized gradient. The diagram below is one example of a performance comparison of all the optimizers.
Numerical Example
Let's see an example of Adam optimizer. A sample dataset is shown below which is the weight and height of a couple of people. We have to predict the height of a person based on the given weight.
| Weight | 60 | 76 | 85 | 76 | 50 | 55 | 100 | 105 | 45 | 78 | 57 | 91 | 69 | 74 | 112 |
| Height | 76 | 72.3 | 88 | 60 | 79 | 47 | 67 | 66 | 65 | 61 | 68 | 56 | 75 | 57 | 76 |
The hypothesis function is;
The cost function is;
The optimization problem is defined as, we must find the values of theta which help to minimize the objective function mentioned below;
The cost function with respect to the weights and are;
The initial values of will be set to [10, 1] and the learning rate , is set to 0.01 and setting the parameters , , and as 0.94, 0.9878 and 10^-8 respectively.
Iteration 1:
Starting from the first data sample the gradients are;
Here and are initially zero, and are calculated as
The new bias-corrected values of and are;
Finally, the weight update is;
The procedure is repeated until the parameters are converged giving values for as [11.39,2].
Applications
The Adam optimization algorithm is the replacement optimization algorithm for SGD for training DNN. According to the author John Pomerat, Aviv Segev, and Rituparna Datta, Adam combines the best properties of the AdaGrad and RMSP algorithms to provide an optimization algorithm that can handle sparse gradients on noisy problems.[6] Research has shown that Adam has demonstrated superior experimental performance over all the other optimizers such as AdaGrad, SGD, RMSP, etc. Further research is going on Adaptive optimizers for Federated Learning and their performances are being compared. Federated Learning is a privacy-preserving technique that is an alternative for Machine Learning where data training is done on the device itself without sharing it with the cloud server. A study has been done by the author Aatila Mustapha, Lachgar Mohamed, and Kartit Ali in which different optimizers are compared, and then based on the results, an optimizer is selected that can be used in the future for big data sets.[7] Here AdGrad performed well but, Adam also showed promising results that tell us that Adam doesn't perform well in all cases.
Conclusion
Research has shown that Adam has demonstrated superior experimental performance over all the other optimizers such as AdaGrad, SGD, RMSP, etc in DNN.[8] This type of optimizer is useful for large datasets. As we know this optimizer is a combination of Momentum and RMSP optimization algorithms. This method is pretty much straightforward, easy to use, and requires less memory. Also, we have shown an example where all the optimizers are compared, and the results are shown with the help of the graph. Overall, it is a robust optimizer and well suited for non-convex optimization problems in the field of Machine Learning and Deep Learning. [9]
References
- ↑ A. Agnes Lydia and , F. Sagayaraj Francis, Adagrad - An Optimizer for Stochastic Gradient Descent, Department of Computer Science and Engineering, Pondicherry Engineering College, May 2019.
- ↑ Tijmen Tieleman and Geoffrey Hinton. Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. COURSERA: neural networks for machine learning, 4(2):26–31, 2012.
- ↑ John Pomerat, Aviv Segev, and Rituparna Datta, On Neural Network Activation Functions and Optimizers in Relation to Polynomial Regression, 2019 IEEE International Conference on Big Data (Big Data).
- ↑ Zijun Zhang, Improved Adam Optimizer for Deep Neural Networks, ©2018 IEEE.
- ↑ Wendyam Eric Lionel Ilboudo, Taisuke Kobayashi, Kenji Sugimoto, TAdam: A Robust Stochastic Gradient Optimizer, [cs.LG] 3 Mar 2020.
- ↑ Diederik P. Kingma, Jimmy Lei Ba, Adam: A Method For Stochastic Optimization, Published as a conference paper at ICLR 2015.
- ↑ AATILA Mustapha, LACHGAR Mohamed and KARTIT Ali, Comparative study of optimization techniques in deep learning: Application in the ophthalmology field, The International Conference on Mathematics & Data Science (ICMDS) 2020.
- ↑ Duchi, J., Hazan, E., & Singer, Y. (2011). Adaptive subgradient methods for online learning and stochastic optimization. Journal of machine learning research.
- ↑ Ameer Hamza Khan, Xinwei Cao, Shuai Li, Vasilios N. Katsikis, and Liefa Liao, Bas-Adam: An Adam Based Approach to Improve the Performance of Beetle Antennae Search Optimizer, IEEE/CAA JOURNAL OF AUTOMATICA SINICA, VOL. 7, NO. 2, MARCH 2020.











































