Adam
Authors: Nicholas Kincaid (CHEME 6800 Fall 2020)
Steward: Fengqi You
Introduction
Adam is a variant of gradient descent that has become widely popular in the machine learning community. Presented in 2015, the Adam algorithm is often recommended as the default algorithm for training neural networks as it has shown improved performance over other variants of gradient descent algorithms for a wide range of problems. Adam's name is derived from adaptive moment estimation because uses estimates of the first and second moments of the gradient to perform updates, which can be seen as incorporating gradient descent with momentum (the first-order moment) and RMSProp algorithm (the second-order moment).
Background
Batch Gradient Descent
In standard batch gradient descent, the parameters, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} , of the objective function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\theta)} , are updated based on the gradient of with respect to Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \theta } for the entire training dataset, as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_t = \theta_{t-1} - \alpha g_t , }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} is defined as the learning rate and is a hyper-parameter of the optimization algorithm, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} is the iteration number.
Stochastic Gradient Descent
Another variant of gradient descent is stochastic gradient descent (SGD), the gradient is computed and parameters are updated as in equation 1, but for each training sample in the training set.
Mini-Batch Gradient Descent
In between batch gradient descent and stochastic gradient descent, mini-batch gradient descent computes parameters updates on the gradient computed from a subset of the training set, where the size of the subset is often referred to as the batch size. Key challenges of the standard gradient descent methods are the tendency to get stuck in local minima and/or saddle points of the objective function, as well as choosing a proper learning rate, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} , which can lead to poor convergence.
Adam Algorithm
The Adam algorithm first computes the gradient, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_t} of the objective function with respect to the parameters Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} , but then computes and stores first and second order moments of the gradient, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_t} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_t} respectively, as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_t = \beta_1 \cdot m_{t-1} + (1-\beta_1) \cdot g_t }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_t = \beta_2 \cdot v_{t-1} + (1-\beta_2) \cdot g_t^2, }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_2} are hyper-parameters that are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \in [0,1]} . These parameters can seen as exponential decay rates of the estimated moments, as the previous value is successively multiplied by the value less than 1 in each iteration. The authors of the original paper suggest values Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_1 = 0.9} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_2 = 0.999} . In the current notation, the first iteration of the algorithm is at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t=1} and both, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_0} are initialized to zero. Since both moments are initialized to zero, at early time steps, these values are biased towards zero. To counter this, the authors proposed a corrected update to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_t} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_t} as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{m}_t = m_t / (1-\beta_1 ^t) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{v}_t = v_t / (1-\beta_2 ^t). }
Finally, the parameter update is computed as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_t = \theta_{t-1} - \alpha \cdot \hat{m}_t / (\sqrt{\hat{v}_t} + \epsilon), }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} is a small constant for stability. The authors recommend a value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon=10^{-8}} .
Numerical Example
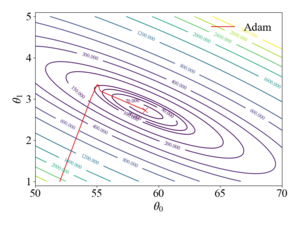
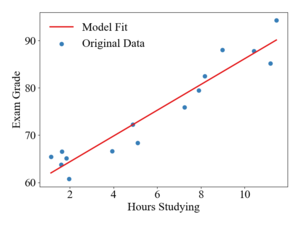
To illustrate how updates occur in the Adam algorithm, consider a linear, least-squares regression problem formulation. The table below shows a sample data-set of student exam grades and the number of hours spent studying for the exam. The goal of this example will be to generate a linear model to predict exam grades as a function of time spent studying.
| Hours Studying | 9.0 | 4.9 | 1.6 | 1.9 | 7.9 | 2.0 | 11.5 | 3.9 | 1.1 | 1.6 | 5.1 | 8.2 | 7.3 | 10.4 | 11.2 |
| Exam Grad | 88.0 | 72.3 | 66.5 | 65.1 | 79.5 | 60.8 | 94.3, | 66.7 | 65.4 | 63.8 | 68.4 | 82.5 | 75.9 | 87.8 | 85.2 |
The hypothesized model function will be
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_\theta(x) = \theta_0 + \theta_1 x.}
The cost function is defined as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J({\theta}) = \frac{1}{2}\sum_i^n \big(f_\theta(x_i) - y_i \big)^2, }
Where the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/2} coefficient is used only to make the derivatives cleaner. The optimization problem can then be formulated as trying to find the values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} that minimize the squared residuals of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_\theta(x)} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{argmin}_{\theta} \quad \frac{1}{n}\sum_{i}^n \big(f_\theta(x_i) - y_i \big) ^2 }
For simplicity, parameters will be updated after every data point i.e. a batch size of 1. For a single data point the derivatives of the cost function with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_1} are
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial J(\theta)}{\partial \theta_0} = \big(f_\theta(x) - y \big) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial J(\theta)}{\partial \theta_1} = \big(f_\theta(x) - y \big) x }
The initial values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\theta}} will be set to [50, 1] and The learning rate, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} , is set to 0.1 and the suggested parameters for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_1} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_2} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} are used. The values for the first two parameter updates are given in Table 2.
The figures to the right show the trajectory of the Adam algorithm over a contour plot of the objective function and the resulting model fit. It should be noted that the stochastic gradient descent algorithm with a learning rate of 0.1 diverges. Even with a rate of 0.01, SGD oscillates around the global minimum due to the large magnitudes of the gradient in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_1} direction.
Application
The Adam optimization algorithm has been widely used in machine learning applications in the context of training neural networks with variety of structures and applications. In their original paper, the authors present three different training examples, logistic regression, multi-layer neural networks for classification of MNIST images, and a convectional neural network (CNN).
Variants of Adam
AdaMax
Nadam
Conclusion
Adam is a variant of the gradient descent algorithm that has been widely adopted in the machine learning community. Adam can be seen as the combination of two other variants of gradient descent, SGD with momentum and RMSProp. Adam uses estimations of the first and second-order moments of the gradient to adapt the parameter update. These moment estimations are computed via moving averages,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_t} andFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_t} , of the gradient and the squared gradient respectfully. In a variety of neural network training applications, Adam has shown increased convergence and robustness over other gradient descent algorithms and is often recommended as the default optimizer for training.
References
- Kingma, Diederik P., and Jimmy Lei Ba. Adam: A Method for Stochastic Optimization. 3rd International Conference on Learning Representations, ICLR 2015 - Conference Track Proceedings, 2015, pp. 1–15.
- Ruder, Sebastian. An Overview of Gradient Descent Optimization Algorithms, 2016, pp. 1–14, http://arxiv.org/abs/1609.04747.
- Tieleman, Tijmen, and Hinton, Geoffrey. Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude, COURSERA: Neural Networks for Machine Learning, 2012.
- Dozat, Timothy. Incorporating Nesterov Momentum into Adam. ICLR Workshop, no. 1, 2016, pp. 2013–16.
- Nesterov, Yuri. A method of solving a convex programming problem with convergence rate O(1/k^2). In Soviet Mathematics Doklady, 1983, pp. 372-376.

