Disjunctive inequalities

Authors: Derek Moore, Grant Logan, Matthew Dinh, Daniel Ladron (SYSEN 5800/CHEME 6800 Fall 2021)

Introduction

Disjunctive inequalities are a form of disjunctive constraints that can be applied to linear programming. Disjunctive constraints are applied in all disjunctive programming, which just refers to the use of logical constraints in linear inequalities, which include “Or,” And,” or "Complement of" statements. In order to solve a disjunctive, the constraints have to be converted into mixed-integer programming (MIP) or mixed-inter linear programming (MILP) constraints, which is called disjunction. Disjunction involves the implementation of a binary variable to create a new set of constraints that can be solved easily. Two common methods for disjunction are the Big-M Reformulation and the Convex-Hull Reformulation.

Method

General

When given a set of inequalities, such as $f_{1}(x)\leq 0\ \ \And \ \ f_{2}(x)\leq 0$, the disjunctive form is given by:  ${\begin{bmatrix}y\\f_{1}(x)\leq 0\end{bmatrix}}\lor {\begin{bmatrix}\neg y\\f_{2}(x)\leq 0\end{bmatrix}}.$ In order to turn the problem into a solvable MIP or MILP, logical constraints are created by using sufficiently large numbers, such as $M_{1}$ and $M_{2}$, and a binary variable y for each inequality. This is shown below by $M$, $y_{1}$, and $y_{2}$:

$f_{1}(x)\leq M\ast (1-y_{1})$

$f_{2}(x)\leq M\ast (1-y_{2})$

To set the binary variable to be mutually exclusive, the sum of the variables is set to 1 and the range is set to {0,1}.

$y_{1}+y_{2}=1$

$y_{1},y_{2}\ \epsilon \ \{0,1\}\ \$

Big-M Reformulation

Figure 1: Disjunctive inequality solution space that can be solved via disjunction using the Big-M Reformulation or the Convex-Hull Reformulation

For the Big-M reformulation, a sufficiently large number, $M$, is used to nullify one set of constraints. This is accomplished by adding or subtracting the term “$M*(1-y)$” to the upper bound and lower bound constraints, respectively, with its respective binary variable. While choosing a large M value allows for isolation, the large value also yields poor relaxation of the model space.

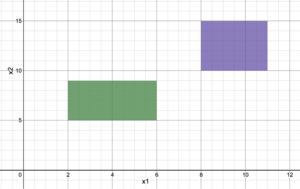
For example, given a solution space ${\begin{bmatrix}y\\2\leq x_{1}\leq 6\\5\leq x_{2}\leq 9\end{bmatrix}}\lor {\begin{bmatrix}\neg y\\8\leq x_{1}\leq 11\\10\leq x_{2}\leq 15\ \end{bmatrix}}$(shown graphically in Figure 1), to determine which of the solutions is optimal, the problem must be formulated such that one set of constraints is chosen. Using the Big-M Reformulation, the following MILP set would be obtained:

y Formulation

$2-M*(1-y_{1})\leq x1\leq 6+M*(1-y_{1})$

$5-M*(1-y_{1})\leq x2\leq 9+M*(1-y_{1})$

-y Formulation

$8-M*(1-y_{2})\leq x1\leq 11+M*(1-y_{2})$

$10-M*(1-y_{2})\leq x2\leq 15+M*(1-y_{2})$

Convex-Hull Reformulation

Similar to the Big-M reformulation, the convex-hull reformulation uses a binary variable, y, to constrain the set of inequalities. The first step in converting the problem into a solvable MILP is breaking all variables into a set of variables, such as ($x_{1}$ → $x_{11}$ + $x_{12}$). By adding these addition variables, it is possible to isolate what set of parameters provide for the optimal solution of the problem. Then, similar to the Big-M reformulation, a sufficiently large variable, M, is used to nullify the non-optimal variable set, such as $x_{11}$ and $x_{12}$. For the problem show in Figure 1, the following variable constraints would be formulated:

y Formulation

$0\leq x_{11}\leq M*y_{1}$

$0\leq x_{21}\leq M*y_{1}$

-y Formulation

$0\leq x_{12}\leq M*y_{2}$

$0\leq x_{22}\leq M*y_{2}$

Formulation of the numerical constraints would then be implemented: y Formulation

$2\ast y_{1}\leq \ x_{11}\ \leq 6\ast y_{1}$

$5\ast y_{1}\leq \ x_{21}\ \leq 9\ast y_{1}$

-y Formulation

$8\ast y_{2}\leq \ x_{12}\ \leq 11\ast y_{2}$

$10\ast y_{2}\leq \ x_{22}\ \leq 15\ast y_{2}$

With the Convex-Hull transformation, the additional constraints confine the problem, such that a tighter (convex) solution space is examined compared to Big-M Formulation.

Examples

Example 1: Location for a Farmer Market

An example of a disjunctive inequality that involves m possible locations for a Farmers Market and n customers who would like to purchase produce from those Farmers. This is convenient for customers who want to purchase produces from local farmers. There is a fix cost to supplying each farmers market with produce from local farmers as well as a capacity. There are also demands from customers on what produces they want. This example of disjunctive inequality is to determine why a farmers market is needed at location i for customers j.

${\begin{bmatrix}\sum _{j}x_{ij}\leq L_{i}\\0\leq x_{ij}\leq P_{ij},\forall j\\G_{i}\leq f_{i}+\sum _{j}l_{ij}\end{bmatrix}}\lor {\begin{bmatrix}x_{ij}=0,\forall j\\G_{i}\geq 0\end{bmatrix}}$

$P_{ij}=$ is the capacity of the transportation from farmer market i to customer j

$x_{ij}=$ is the number of produced bought by the customer j from the farmer market i

$G_{i}=$ is the amount of purchases at farmer markets i

$f_{i}=$ is the fixed cost for farmers market i

$L_{i}=$ is the capacity amount of farmer markets i

$l_{ij}=$ is the fixed cost for transportation from farmers market i to customer j

Redefining this problem into a Convex Hull form requires defining binary variables involved with each case and setting their summation to 1. For new variables derived from the original variables are created for use in each case.

$x_{ij}=x_{ij1}+x_{ij2}$

$G_{i}=G_{i1}+G_{i2}$

Now nullify the non-optimal variable sets with a large M:

$0\leq x_{ij1}\leq y_{1}M$

$0\leq x_{ij2}\leq y_{2}M$

$0\leq G_{i1}\leq y_{1}M$

$0\leq G_{i2}\leq y_{2}M$

The number of produce shipped to a farmers market $x_{ij}$ is constraint by $L_{i}$ due to the capacity of produce the farmer market can hold. The number produce shipped is also constraint by it's own capacity $P_{ij}$ that it can hold during the transportation process.

$0\leq x_{ij2}\leq P_{ij}$

$\sum _{j}x_{ij1}\leq L_{i}$

The total cost $G_{i}$ will be greater than the sum of the fixed cost of the farmers market and the capacity of the farmers market.

$G_{i}\geq f_{i}+\sum _{j}L_{ij}$

Thus, the result is there cannot be a farmers market $x_{ij2}$ at this location of $i$

$x_{ij2}=0$

Finally, the farmers market can be located in this location of $i$ for $G_{i2}$

$G_{i2}\geq 0$, ${\begin{bmatrix}x_{ij}=0,\forall j\\G_{i}\geq 0\end{bmatrix}}$

Applications

Figure 2: Wastewater system

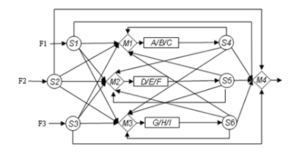
GDP formulations can be used to identify real world problems. Below in Figure 2, shows a wastewater network that removes pollutants from its mixture. The task is to figure out the total cost to discharge the pollution.

This wastewater system can be reformulated into a non-convex General Disjunction Programming problem shown below:

$MinZ=\textstyle \sum _{k\epsilon PU}CP_{k}\displaystyle$

$f_{k}^{j}=\textstyle \sum _{i\epsilon M_{k}}f_{i}^{j}\displaystyle$ $\forall jk\in MU$

$\textstyle \sum _{i\epsilon S_{k}}f_{i}^{j}\displaystyle =f_{k}^{j}$ $\forall jk\in SU$

$\textstyle \sum _{i\epsilon S_{k}}\zeta _{i}^{j}\displaystyle =1$ $k\in SU$

$f_{k}^{j}=\textstyle \zeta _{i}^{k}f_{k}^{j}\forall _{j}\displaystyle$ $i\in S_{k}$ $k\in SU$

${\underset {h\epsilon D_{k}}{\lor }}{\begin{bmatrix}y\\f_{i}^{j}=\mathrm {B} _{i}^{jh},i\epsilon OPU_{k},i^{i}\epsilon IPU_{k},\forall _{j}\\F_{k}=\sum _{j}f_{i}^{j},i\epsilon OPU_{k}\\CP_{k}=\partial _{ik}F_{k}\end{bmatrix}}k\epsilon PU$

$0\leq \zeta _{i}^{k}\leq 1$ $\forall j,k$

$0\leq f_{i}^{j},f_{k}^{j}$ $\forall i,j,k$

$0\leq CP_{k}$ $\forall k$

$YP_{k}^{h}\in$ {True, False} $\forall h\in D_{k}\forall k\in PU$

Conclusion

As shown, disjunctive inequalities can be used to generate all valid inequalities for an integer program. A simple disjunctive procedure can be used to generate all valid inequalities for a 0 or 1 mixed-integer program. Two methods that are used to reformulate the problem are Convex Hull and Big-M formulations. It could be shown that to obtain the convex hull of a 0 or 1 mixed-integer program, it suffices to take the convex hull of each 0 or 1 variable at a time . Implementing the Big-M method generates a much smaller MILP/MINLP with a tighter relaxation than the convex-hull method. Disjunctive inequalities can be used to improve the performance of any general purpose Branch-and-Cut algorithm as shown on the research from Balas and Bonami . Most of the real world problems that can be solved through disjunctive inequalities are in chemical engineering or involve process synthesis where a logic decision has to be made to optimize the solution.