Interior-point method for NLP

Author: Apoorv Lal (CHEME 6800, Fall 2021)

Introduction

Interior point (IP) methods mainly emerged in the late 1970's and 1980s. They were developed as algorithms to solve linear programming(LP) problems with a better worst case complexity than the simplex method [2]. In 1984, Karmarkar used IP methods to develop 'A new polynomial-Time method for Linear Programming' [3]. The main advantage of this method was better practical performance than the earlier algorithms like the ellipsoid method by Khachiyan [4]. After Karmarkar's publication more intensive research in this field led to development of a new category of IP methods known as 'primal-dual' methods. Currently, most powerful type of primal-dual codes are Ipopt, KNITRO and LOQO [2].

In recent years the majority of research in the field of IPs is for nonlinear optimisation problems, especially for second order (referred as SOCO) and semidefinite optimisation ( referred as SDO). SDO has wide range of applications in combinatorial optimization, control, structural engineering and electrical engineering [1].

Theory & Methodology

Nonlinear Constrained Optimisation

General form for the nonlinear constrained optimisation problem

• The objective function and constraints can be any linear, quadratic or any general nonlinear functions
• Typically, applied for convex optimisation problems
• Convert maximisation problems to minimisation problems by taking negative of the objective function
• Convert any general inequalities to simple inequalities using slack variables.

Slack variables

Figure 2: Constrained non linear optimisation problem without slack variables.

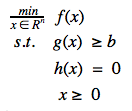
Consider a general equation of the form as shown in Figure 2. Now we need to convert this form to the form as shown in figure 1. For this the inequality g(x) ≥ b can be written g(x) - b ≥ 0 which can be further written as:

g(x) - b - s = 0 along with

s ≥ 0

Thus the set of equation g(x) - b - s = 0 and h(x) = 0 become c(x) = 0 as shown in figure 1.

References

[1] Nonlinear Optimization, Immanuel M Bomze,Roger Fletcher...

[2] AN INTERIOR-POINT METHOD FOR NONLINEAR OPTIMIZATION PROBLEMS WITH LOCATABLE AND SEPARABLE NONSMOOTHNESS, MARTIN SCHMIDT

[3] Narendra Karmarkar. “A New Polynomial-Time Algorithm for Linear Programming.” In: Combinatorica 4.4 (1984), pp. 373–395. issn: 0209-9683. doi:10.1007/BF02579150.

[4] Leonid Genrikhovich Khachiyan. “A polynomial algorithm in linear program- ming.” In: Soviet Mathematics Doklady 20 (1979), pp. 191–194.